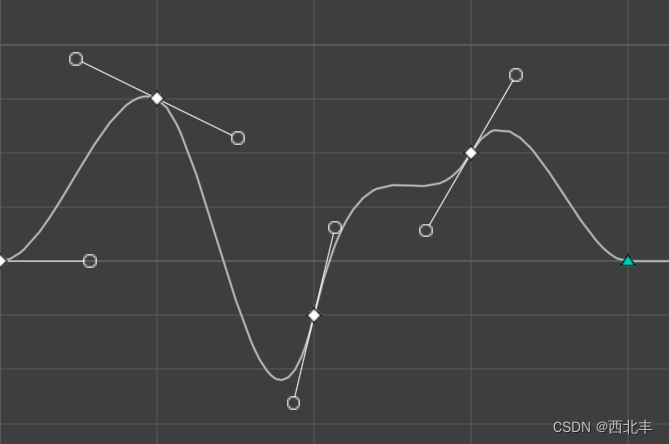
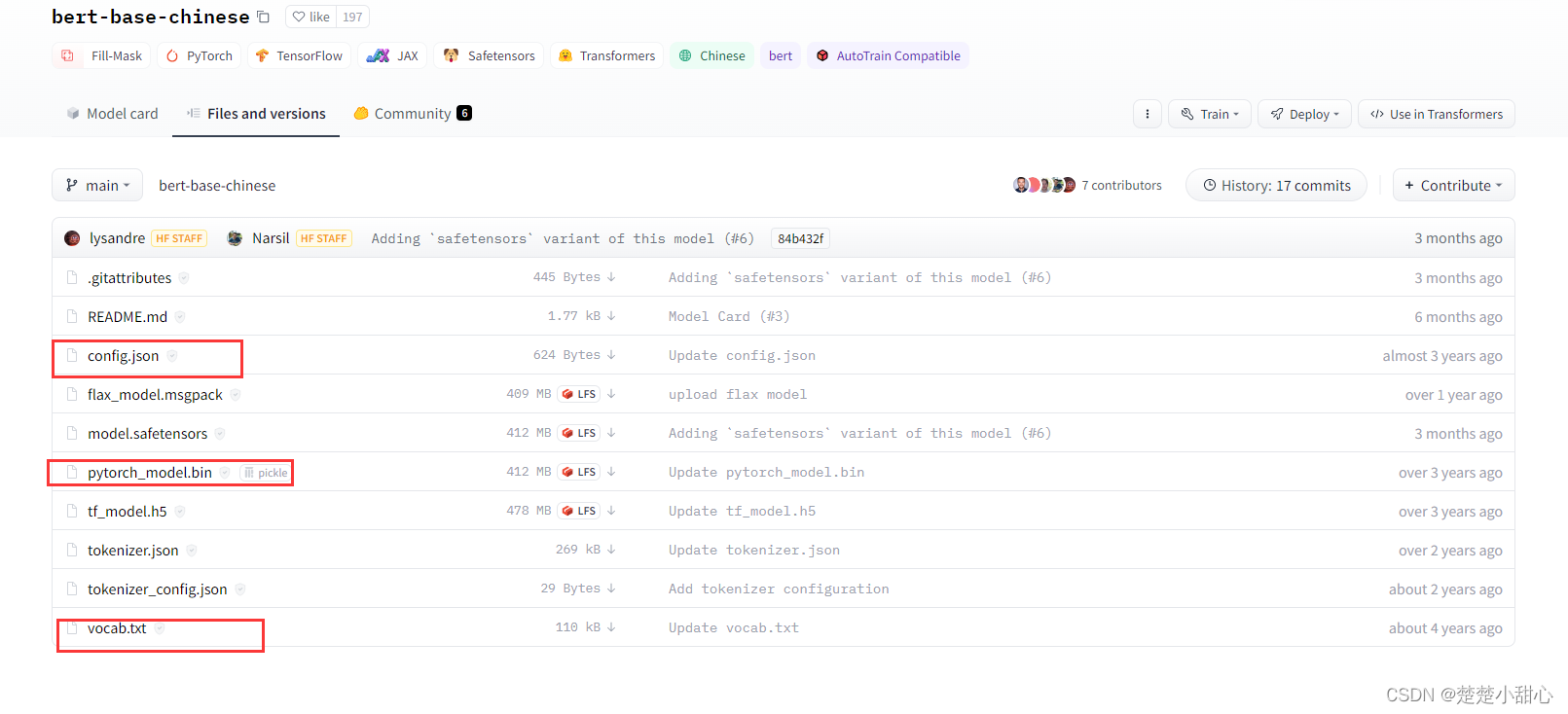
三次样条
已知有一组点 x 0 , x 1 , x 2 , ⋯ , x n x_0, x_1, x_2, \cdots, x_n x0,x1,x2,⋯,xn, 其中, x t < x t + 1 x_t<x_{t+1} xt<xt+1, y ( x t ) = y t y(x_t)=y_t y(xt)=yt, 及该点处的切线 y ′ ( x t ) = y t ′ y'(x_t)=y'_t y′(xt)=yt′
每两个相邻的点之间可以作一个三次曲线
在所有相邻点之间的三次曲线连起来就构成了一个三次样条(Cubic spline)
三次样条是二阶可导的
设三次曲线由两个相邻的点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0),
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1)及其切线
y
0
′
y'_0
y0′,
y
1
′
y'_1
y1′确定
其函数为
y
=
a
x
3
+
b
x
2
+
c
x
+
d
y=ax^3+bx^2+cx+d
y=ax3+bx2+cx+d, 导函数为
y
′
=
3
a
x
2
+
2
b
x
+
c
y'=3ax^2+2bx+c
y′=3ax2+2bx+c, 其中
x
∈
[
x
0
,
x
1
]
x\in[x_0, x_1]
x∈[x0,x1]
可列得方程组
{
3
a
x
0
2
+
2
b
x
0
+
c
=
y
0
′
3
a
x
1
2
+
2
b
x
1
+
c
=
y
1
′
a
x
0
3
+
b
x
0
2
+
c
x
0
+
d
=
y
0
a
x
1
3
+
b
x
1
2
+
c
x
1
+
d
=
y
1
\left\{\begin{matrix} 3ax_0^2 & + 2bx_0 & + c &&= y_0' \\ 3ax_1^2 & + 2bx_1 & + c &&= y_1' \\ ax_0^3 & + bx_0^2 & + cx_0 & + d &= y_0 \\ ax_1^3 & + bx_1^2 & + cx_1 & + d &= y_1 \\ \end{matrix}\right.
⎩
⎨
⎧3ax023ax12ax03ax13+2bx0+2bx1+bx02+bx12+c+c+cx0+cx1+d+d=y0′=y1′=y0=y1
将系数
a
,
b
,
c
,
d
a,b, c, d
a,b,c,d分离出来写成矩阵, 得到
(
3
x
0
2
2
x
0
1
0
3
x
1
2
2
x
1
1
0
x
0
3
x
0
2
x
0
1
x
1
3
x
1
2
x
1
1
)
(
a
b
c
d
)
=
(
y
0
′
y
1
′
y
0
y
1
)
\begin{pmatrix} 3x_0^2 & 2x_0 & 1 & 0\\ 3x_1^2 & 2x_1 & 1 & 0\\ x_0^3 & x_0^2 & x_0 & 1 \\ x_1^3 & x_1^2 & x_1 & 1 \\ \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ d \end{pmatrix} = \begin{pmatrix} y_0' \\ y_1' \\ y_0 \\ y_1 \end{pmatrix}
3x023x12x03x132x02x1x02x1211x0x10011
abcd
=
y0′y1′y0y1
设
A
=
∣
3
x
0
2
2
x
0
1
0
3
x
1
2
2
x
1
1
0
x
0
3
x
0
2
x
0
1
x
1
3
x
1
2
x
1
1
∣
A = \begin{vmatrix} 3x_0^2 & 2x_0 & 1 & 0\\ 3x_1^2 & 2x_1 & 1 & 0\\ x_0^3 & x_0^2 & x_0 & 1 \\ x_1^3 & x_1^2 & x_1 & 1 \\ \end{vmatrix}
A=
3x023x12x03x132x02x1x02x1211x0x10011
解得
a
=
∣
y
0
′
2
x
0
1
0
y
1
′
2
x
1
1
0
y
0
x
0
2
x
0
1
y
1
x
1
2
x
1
1
∣
A
b
=
∣
3
x
0
2
y
0
′
1
0
3
x
1
2
y
1
′
1
0
x
0
3
y
0
x
0
1
x
1
3
y
1
x
1
1
∣
A
c
=
∣
3
x
0
2
2
x
0
y
0
′
0
3
x
1
2
2
x
1
y
1
′
0
x
0
3
x
0
2
y
0
1
x
1
3
x
1
2
y
1
1
∣
A
d
=
∣
3
x
0
2
2
x
0
1
y
0
′
3
x
1
2
2
x
1
1
y
1
′
x
0
3
x
0
2
x
0
y
0
x
1
3
x
1
2
x
1
y
1
∣
A
a = \frac{ \begin{vmatrix} y_0' & 2x_0 & 1 & 0\\ y_1' & 2x_1 & 1 & 0\\ y_0 & x_0^2 & x_0 & 1 \\ y_1 & x_1^2 & x_1 & 1 \\ \end{vmatrix} }{A} \\ b = \frac{ \begin{vmatrix} 3x_0^2 & y_0' & 1 & 0\\ 3x_1^2 & y_1' & 1 & 0\\ x_0^3 & y_0 & x_0 & 1 \\ x_1^3 & y_1 & x_1 & 1 \\ \end{vmatrix} }{A} \\ c = \frac{ \begin{vmatrix} 3x_0^2 & 2x_0 & y_0' & 0\\ 3x_1^2 & 2x_1 & y_1' & 0\\ x_0^3 & x_0^2 & y_0 & 1 \\ x_1^3 & x_1^2 & y_1 & 1 \\ \end{vmatrix} }{A} \\ d = \frac{ \begin{vmatrix} 3x_0^2 & 2x_0 & 1 & y_0'\\ 3x_1^2 & 2x_1 & 1 & y_1'\\ x_0^3 & x_0^2 & x_0 & y_0 \\ x_1^3 & x_1^2 & x_1 & y_1 \\ \end{vmatrix} }{A}
a=A
y0′y1′y0y12x02x1x02x1211x0x10011
b=A
3x023x12x03x13y0′y1′y0y111x0x10011
c=A
3x023x12x03x132x02x1x02x12y0′y1′y0y10011
d=A
3x023x12x03x132x02x1x02x1211x0x1y0′y1′y0y1
最后三次样条曲线可用下式表达
y
=
{
a
0
x
3
+
b
0
x
2
+
c
0
x
+
d
0
x
∈
[
x
0
,
x
1
]
a
1
x
3
+
b
1
x
2
+
c
1
x
+
d
1
x
∈
[
x
1
,
x
2
]
⋯
a
t
x
3
+
b
t
x
2
+
c
t
x
+
d
t
x
∈
[
x
t
,
x
t
+
1
]
⋯
a
n
−
1
x
3
+
b
n
−
1
x
2
+
c
n
−
1
x
+
d
n
−
1
x
∈
[
x
n
−
1
,
x
n
]
y=\left\{\begin{matrix} a_0x^3+b_0x^2+c_0x+d_0 & x\in[x_0,x_1] \\ a_1x^3+b_1x^2+c_1x+d_1 & x\in[x_1,x_2] \\ \cdots \\ a_tx^3+b_tx^2+c_tx+d_t & x\in[x_t,x_{t+1}] \\ \cdots \\ a_{n-1}x^3+b_{n-1}x^2+c_{n-1}x+d_{n-1} & x\in[x_{n-1},x_n] \end{matrix}\right.
y=⎩
⎨
⎧a0x3+b0x2+c0x+d0a1x3+b1x2+c1x+d1⋯atx3+btx2+ctx+dt⋯an−1x3+bn−1x2+cn−1x+dn−1x∈[x0,x1]x∈[x1,x2]x∈[xt,xt+1]x∈[xn−1,xn]