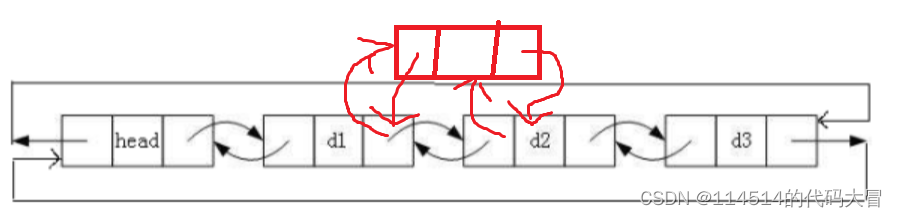
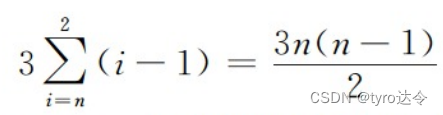诸如环形链表的结构有：

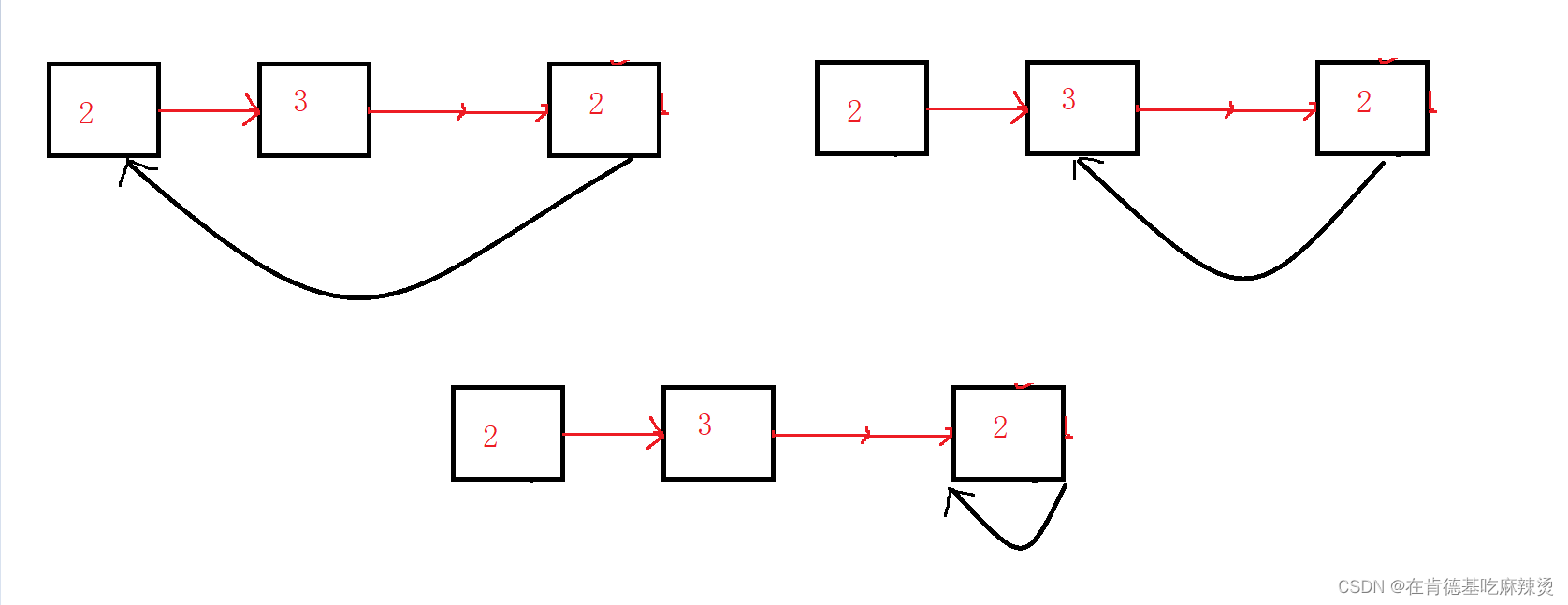
尾节点链接向各个节点的链表，也可链向自己，称为环形链表。

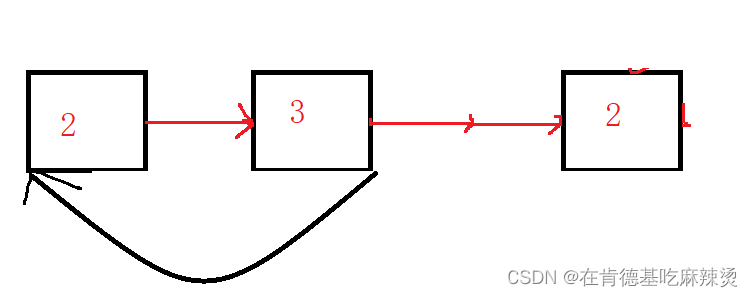
只要链表中带有环，均可称为环形链表。

下面通过一些例题来详细讲述环形链表：

1.

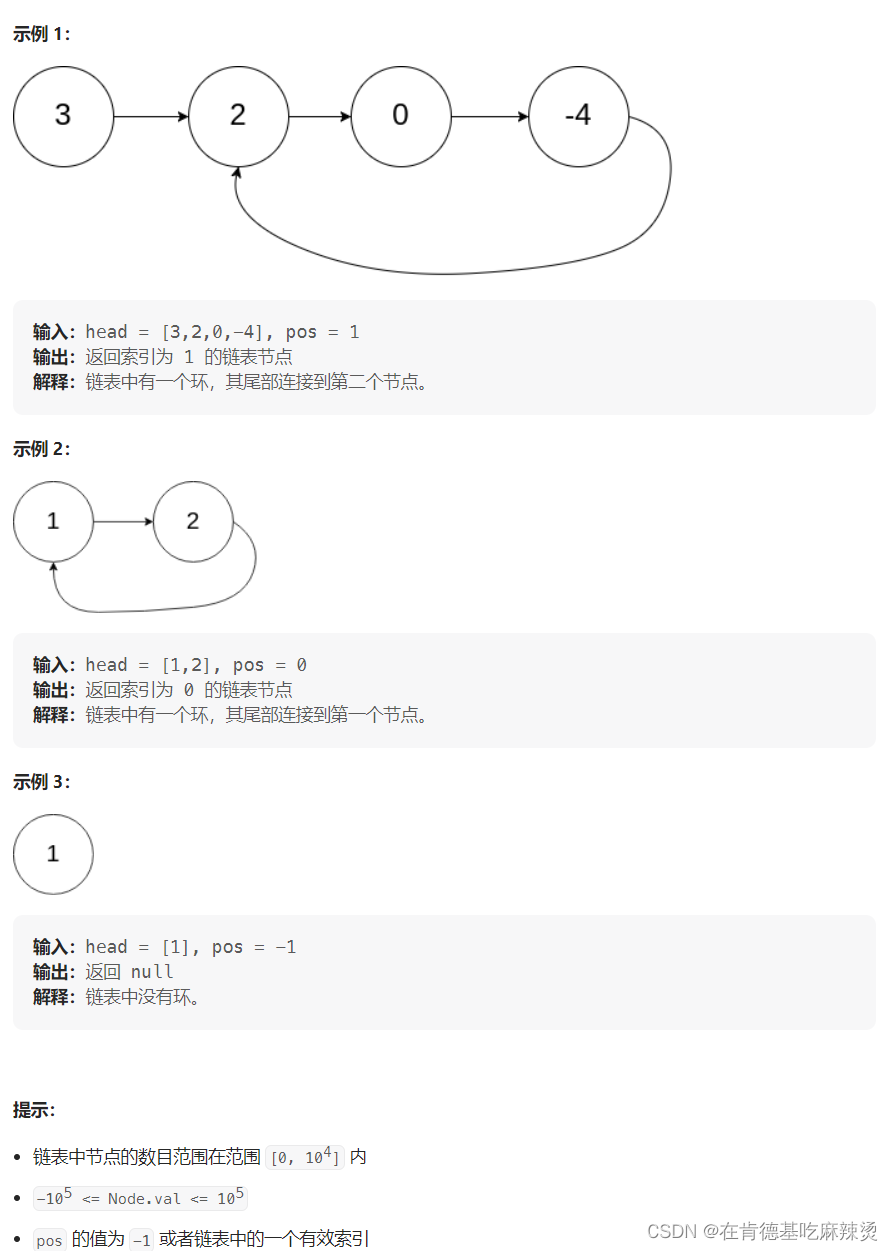
给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

解题思路：使用快慢指针，快指针一次走两步，慢指针一次走一步，当快指针和慢指针相遇时，说明链表带环。

bool hasCycle(struct ListNode *head) 
{
    struct ListNode*fast =head,*slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            return true;
        }
    }
    
    return false;
}

因为快指针总是比慢指针快一步，所以快指针会先进环，慢指针后进环，当慢指针进环时，快指针会在环中先走，此时慢指针一定会在走一圈之前被慢指针追上，因为每走一步，慢指针和快指针之间的距离就会少1。

注意：为什么会是快指针走两步，慢指针走一步呢？快指针走三步，慢指针走一步可以吗？

解析：

我们画一个较为抽象的模型，上面是各个节点，

假如快指针一次走3步，慢指针一次走1步，当快指针进环时，慢指针才走了一点点，在慢指针进环的时候，快指针已经在环里面转了一圈多。此时快指针和慢指针每走一次，它们之间的距离就会少2，现在假设的环的大小是4，那么在慢指针进环后，会相遇，（因为环的大小是偶数，快慢指针每走一次就会少2，是偶数次）。假设环的大小是5时，那么快慢指针就永远不会相遇了，因为快指针不仅会追上慢指针，还会跃过慢指针。

所以快指针走2步，慢指针走1步的方法才是正确的。

2.

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

解题思路：结论：1.先给定一个快指针和一个慢指针，依照上一题的方法，找出它们在环中相遇的位置，并标记下来。

2.一个指针从头开始，一个指针从快慢指针的相遇位置开始，每次走一步，一定会在环形入口点相遇。

证明：

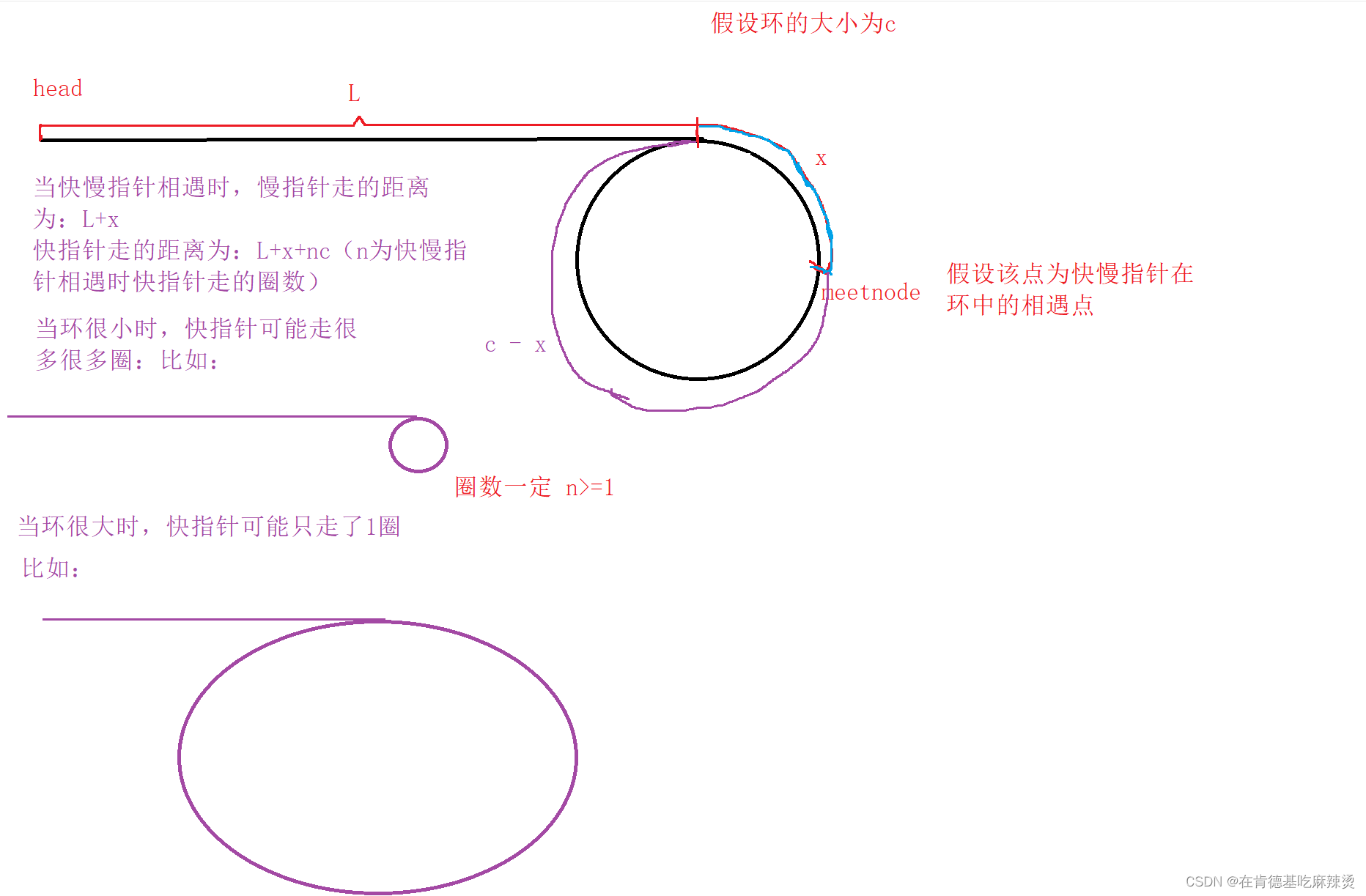
由于快指针的速度是慢指针的两倍，所以快指针走的距离是慢指针走的距离的2倍。

所以有：

2*(L+x) = L+x+n*c

化简一下得： L = n*c - x

改变一下形式得： L = (n-1)*c - x + （n>=1）

最坏的情况，也就是当环很大时，n == 1，此时L = c -x

L = c -x 是什么？

请回到上图， L 是从头开始走的指针走到环形入口的距离，c - x是另一个指针从快慢指针在环中相遇的位置开始走到环形入口点的距离，两者相等！

证明了该结论：

结论：1.先给定一个快指针和一个慢指针，依照上一题的方法，找出它们在环中相遇的位置，并标记下来。

2.一个指针从头开始，一个指针从快慢指针的相遇位置开始，每次走一步，一定会在环形入口点相遇。

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode*fast = head;
    struct ListNode*slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        //相遇
        if(fast == slow)
        {
            struct ListNode*meetnode = slow;
            while(meetnode!=head)
            {
                meetnode = meetnode->next;
                head = head->next;
            }
            //退出循环，说明找到了相交点
            return head;
        }
    }
    //不带环
    return NULL;

}

以上就是有关环形链表的相关知识。