1、插入排序

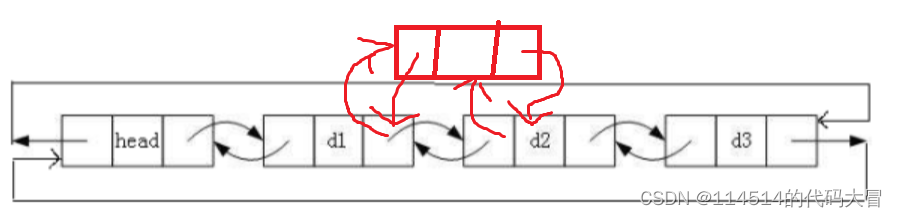
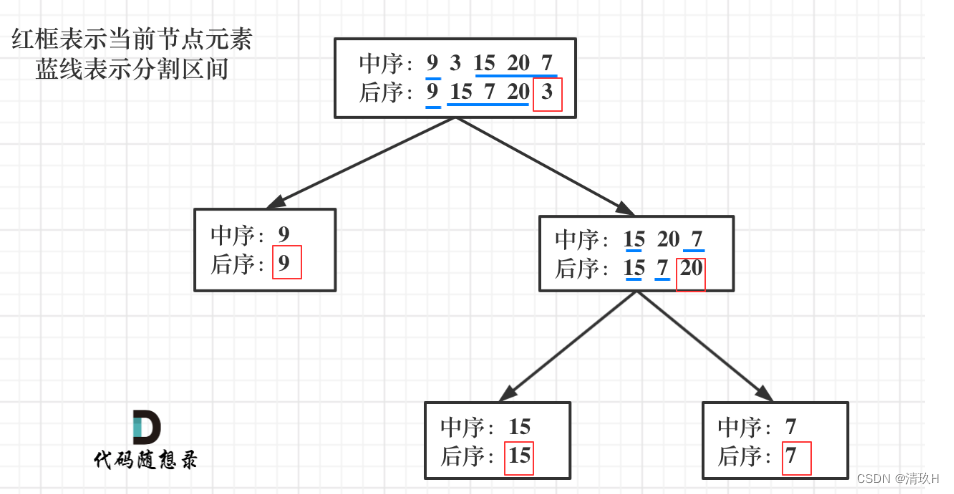
插入排序(insertion sort)的基本操作是将当前无序序列区 R[i…n]中的记录 R[i]“插入”到有序序列区 R[1…i-1]中,使有序序列区的长度增 1,如图所示。

例如,对下列一组记录的关键字:

(49,38,65,76,27,13 ,91,52) （3-4）

进行插人排序的过程中,前 4 个记录已按关键字非递减的顺序有序排列,构成一个含 4 个记录的有序序列

(38 ,49 ,65 ,76) （3-5）

现要将式(3-4)中第 5个(关键字为 27 的)记录插人到式(3-5)的序列中去,以得到一个新的含 5 个记录的有序序列

(27 ,38,49 ,65,76) （3-6）

称这个过程为“一趟插入排序”。

为了防止循环变量出界,在循环结束的条件中加上了(i>=0)的判别,若将这个算法用在插入排序上,将会因为这个条件的判别增加排序的时间。当排序问题的规模较大或经常需要进行排序的应用场合.这一操作的时间开销就该有所计较。利用 L.r[o] 分量“复制”待插入的记录,则在向前查找插入位置时,循环变量就不可能发生出界的情况,称 L.r[0]为“哨兵”。算法如下：

整个插人排序需进行 n-1 趟“插入”。只含一个记录的序列必定是个有序序列,因此插入应从 i=2 起进行。此外,若第i个记录的关键字不小于第 i-1 个记录的关键字，“插入”也就不需要进行了。插入排序的算法如下:

例如,对下列一组关键字进行插入排序过程中,每一趟排序之后的状况如下图所示。

插入排序算法的分析如下:由于在一趟插入排序中,L.r[o].key 至多和 i 个关键字进行比较,再加上“之前”的一次比较,则对于每个“i”至多进行(i+1)次关键字间的比较,而整个插入排序中, i 从2变化到 n ,因此插入排序的时间复杂度为 O(n²)。类似选择排序,整个排序过程中也仅需一个哨兵的辅助空间,所以它的空间复杂度为 O(1)。

显然,如果原始记录已按关键字“非递减顺序”有序排列,则将使插入排序呈现最好状态,在每一趟中仅作一次比较,总的比较次数达到最小值 Cmin =n-1且记录不作移动;反之,如果原始记录是按关键字“非递增顺序”有序(又称“逆序”)排列,则插入排序呈现最坏状态。此时总的比较次数取最大值 Cmax=(n+4)(n-1)/2,并作同样次数的记录移动。

从以上分析可知,当关键字分布情况不同时,算法在执行过程中的时间消耗也颇有差异。在随机情况下,实际的比较次数估计比最坏情况的要少,而且对插入排序而言,关键字分布的有序性越强,比较次数也越少。但对选择排序而言,关键字的分布对比较次数没有影响。

插入排序是稳定的排序方法.

2、起泡排序

起泡排序(bubble sort)的基本思想是通过对无序序列区中的记录进行相邻记录关键字间的“比较”和记录位置的“交换”实现关键字较小的记录向“一头”飘浮，而关键字较大的记录向“另一头”下沉,从而达到记录按关键字非递减顺序有序排列的目标。

假设在排序过程中,记录序列 R[1…n]分为无序序列 R[1…i]和有序序列 R[i+1…n]两个区域,则本趟起泡排序的基本操作是从第1个记录起。比较第 1个记录和第 2个记录的关键字,若呈“逆序”关系,则将两个记录交换,然后比较第 2 个记录和第 3 个记录的关键字若呈“逆序”,则交换之。依此类推,直至比较了 R[i-1] 和 R[i]之后,该无序区中关键字最大的记录将定位在 R[i]的位置上,如下图所示。

一般情况下,整个起泡排序只需进行 k(1<=k<n)趟起泡操作,起泡排序的结束条件是“在某一趟排序过程中没有进行记录交换的操作”。下图展示了起泡排序的一个例子。从图示中可见,在起泡排序的过程中,关键字较小的记录如“起泡”般逐趟往上“飘浮”,而关键字较大的记录如石头般“下沉”,每一趟有一块“最大”的石头沉落水底。

起泡排序算法如下：

分析起泡排序的时间和空间效率,从以上讨论中可知,起泡排序和插入排序一样,对不同组的记录所需进行的关键字间的比较次数和记录的移动次数不同,最好的情况是,原始记录按关键字顺序有序排列,此时只需进行一趟起泡排序,则只进行 n-1次关键字间的比较，且没有移动记录。反之,最坏的情况是,记录按关键字逆序有序排列,此时需进行n-1 趟起泡，整个排序过程中进行的关键字间的比较次数为

记录的移动次数为

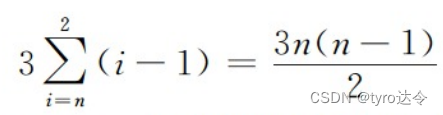
因此,起泡排序的时间复杂度为 O(n)。和选择排序类似,起泡排序的过程中也只需要一个辅助空间,故空间复杂度为 O(1)。

起泡排序也是稳定的排序方法。