目录
1.汉密尔顿图判定的实际问题
判断是否是汉密尔顿图
思考:下图中哪些是汉密尔顿图
例子
2.平面图
平面图的基本概念
并非所有的图都能嵌入平面
平面图的面与次数
欧拉公式
欧拉公式的证明
3.平面图的判定
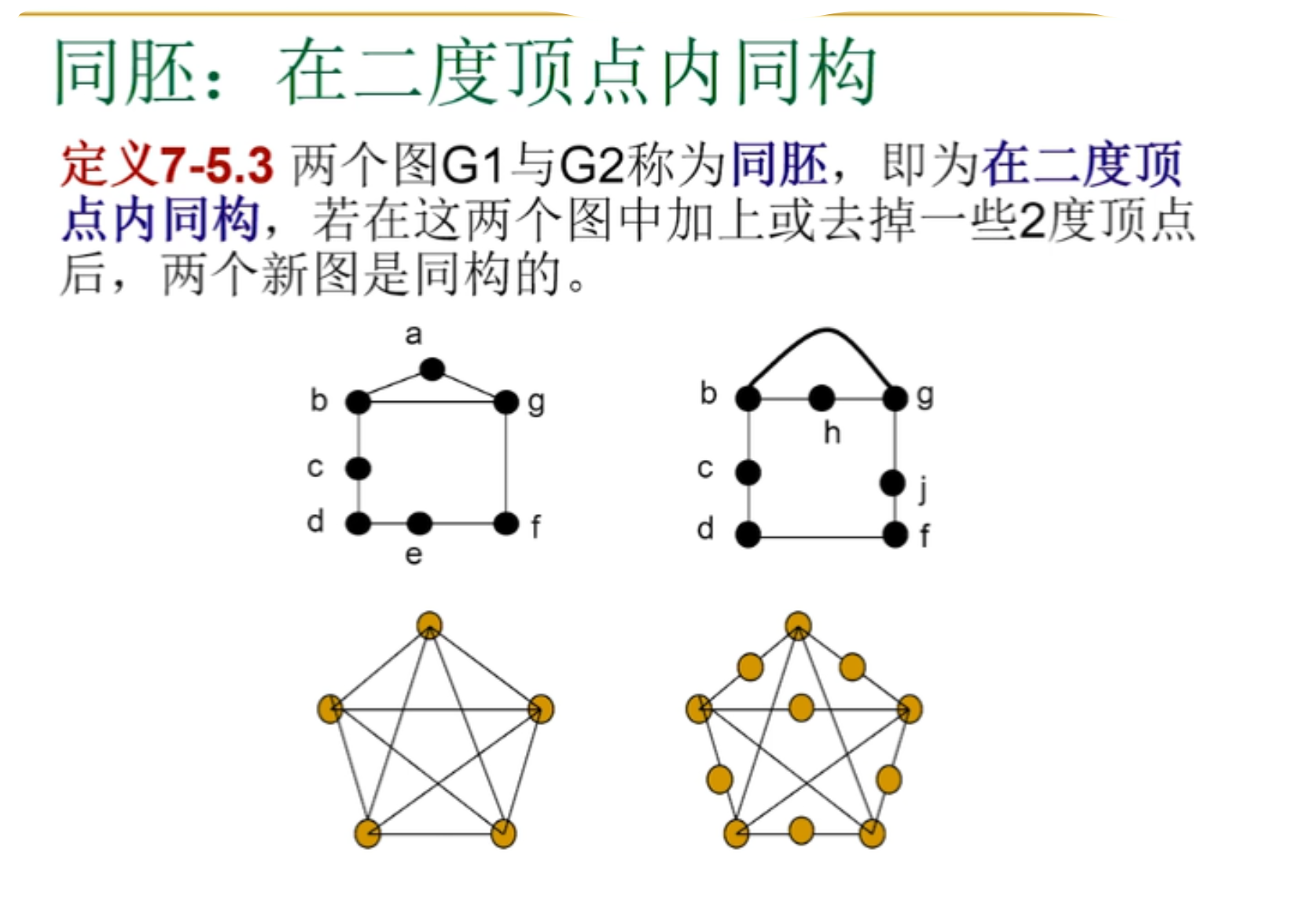
同胚
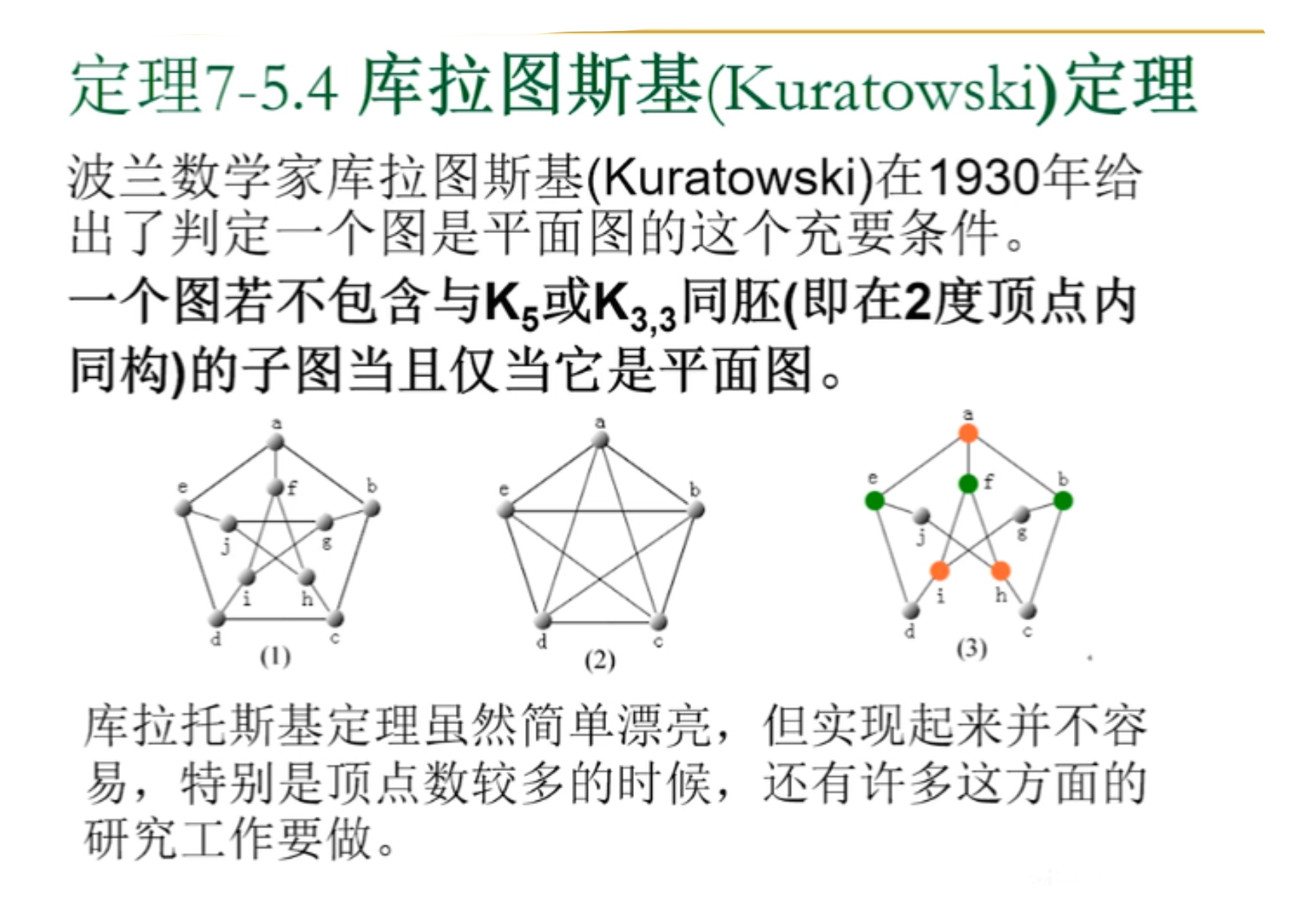
kuratowski定理
4.对偶图
四色定理
平面图的着色
平面图的对偶图
更多的对偶图示例
着色相关定理
平面图的五色定理
5.五色定理的证明
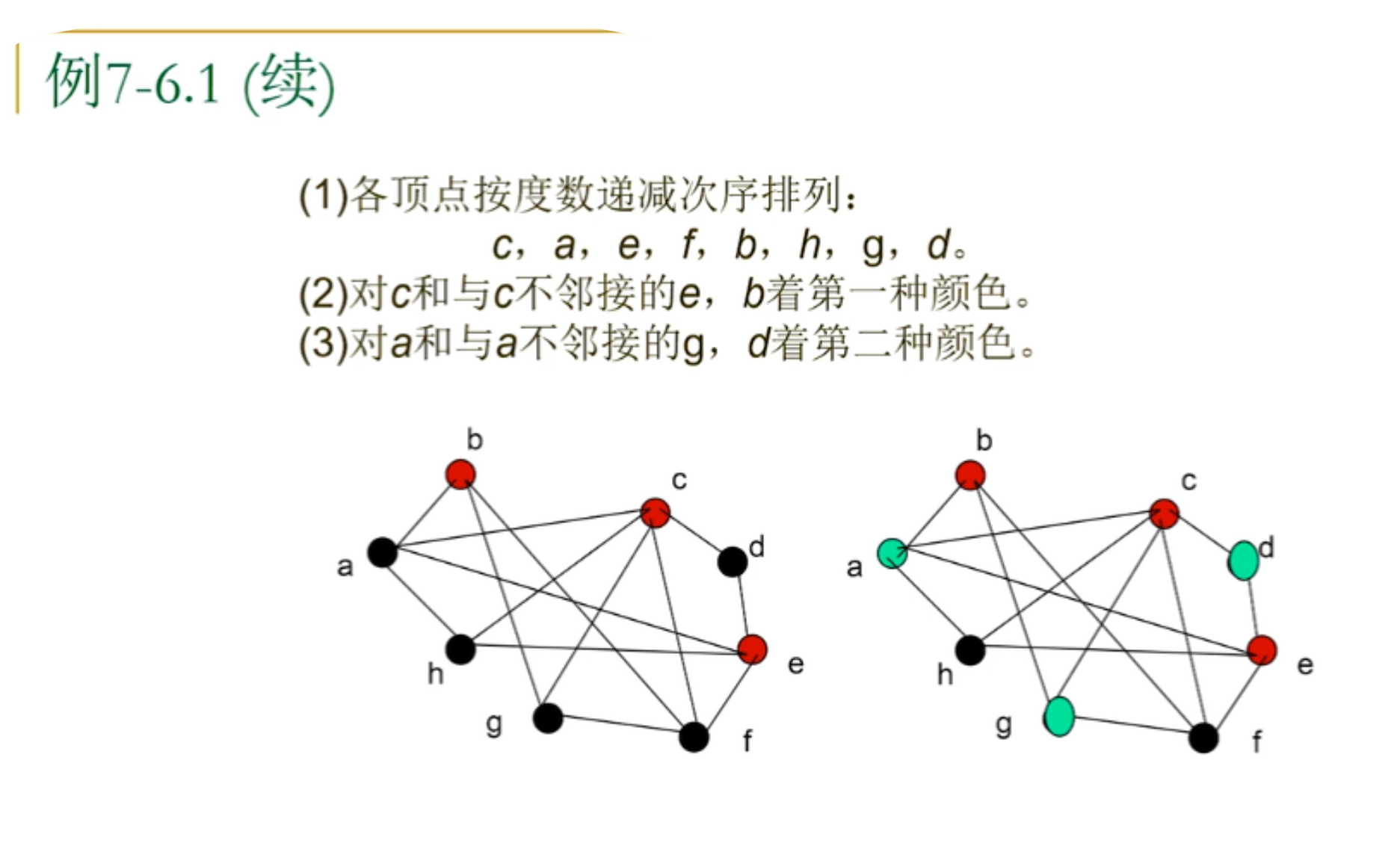
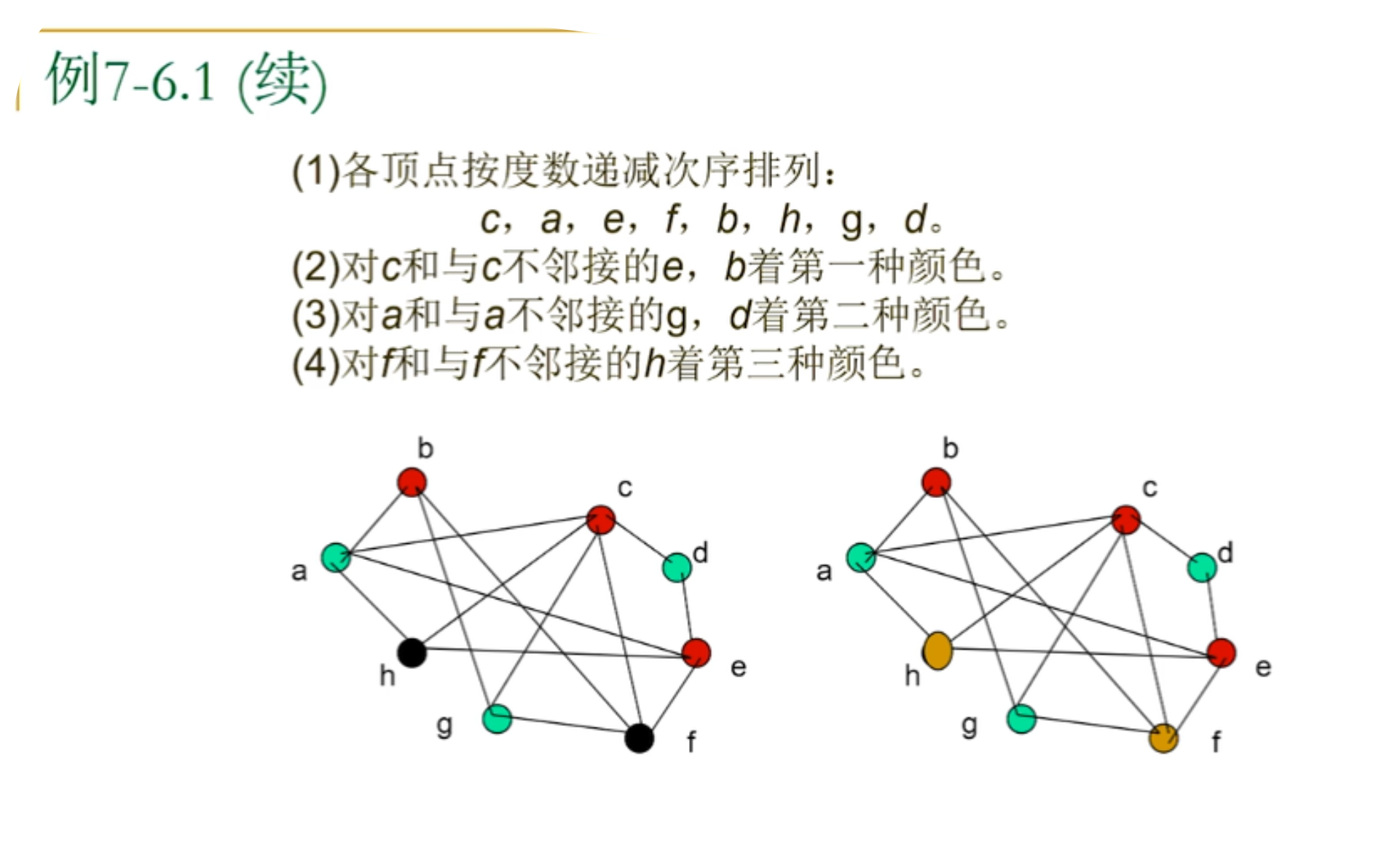
6.WelchPowell着色法
例子
1.汉密尔顿图判定的实际问题
判断是否是汉密尔顿图
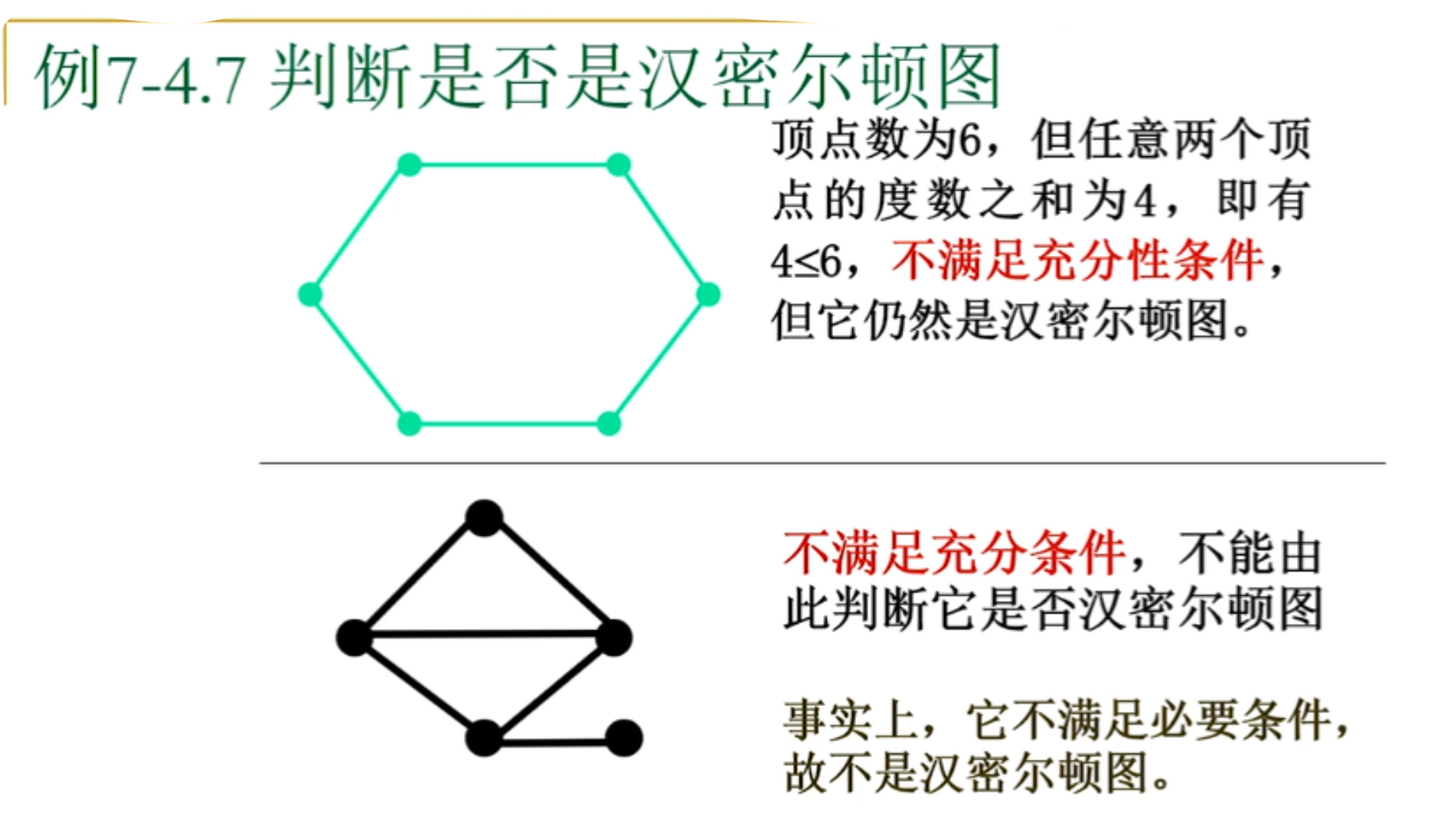
下面的那个图,中间下面的那个点去掉后会形成两个连通图
思考:下图中哪些是汉密尔顿图
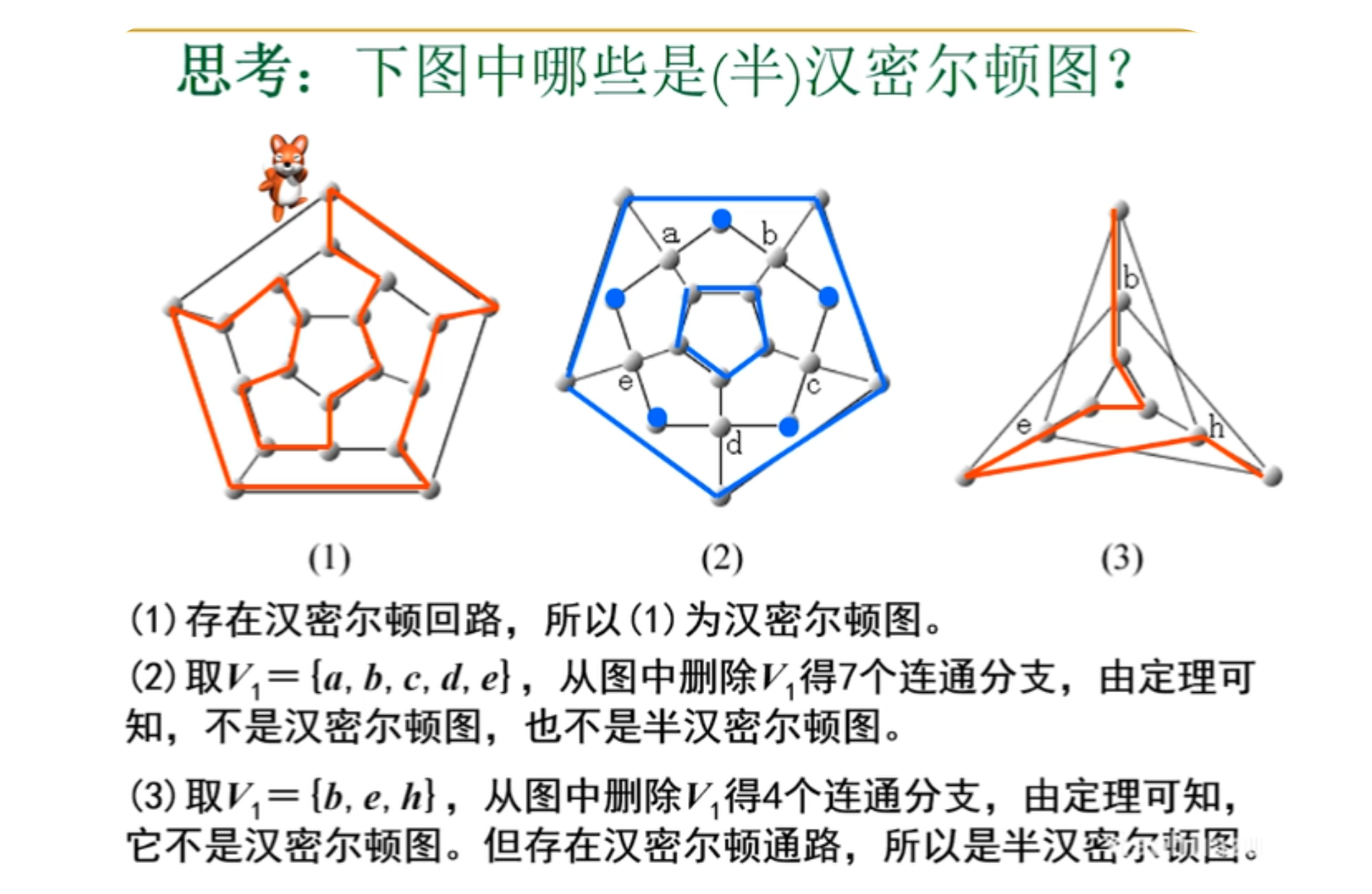
例子


2.平面图
平面图的基本概念
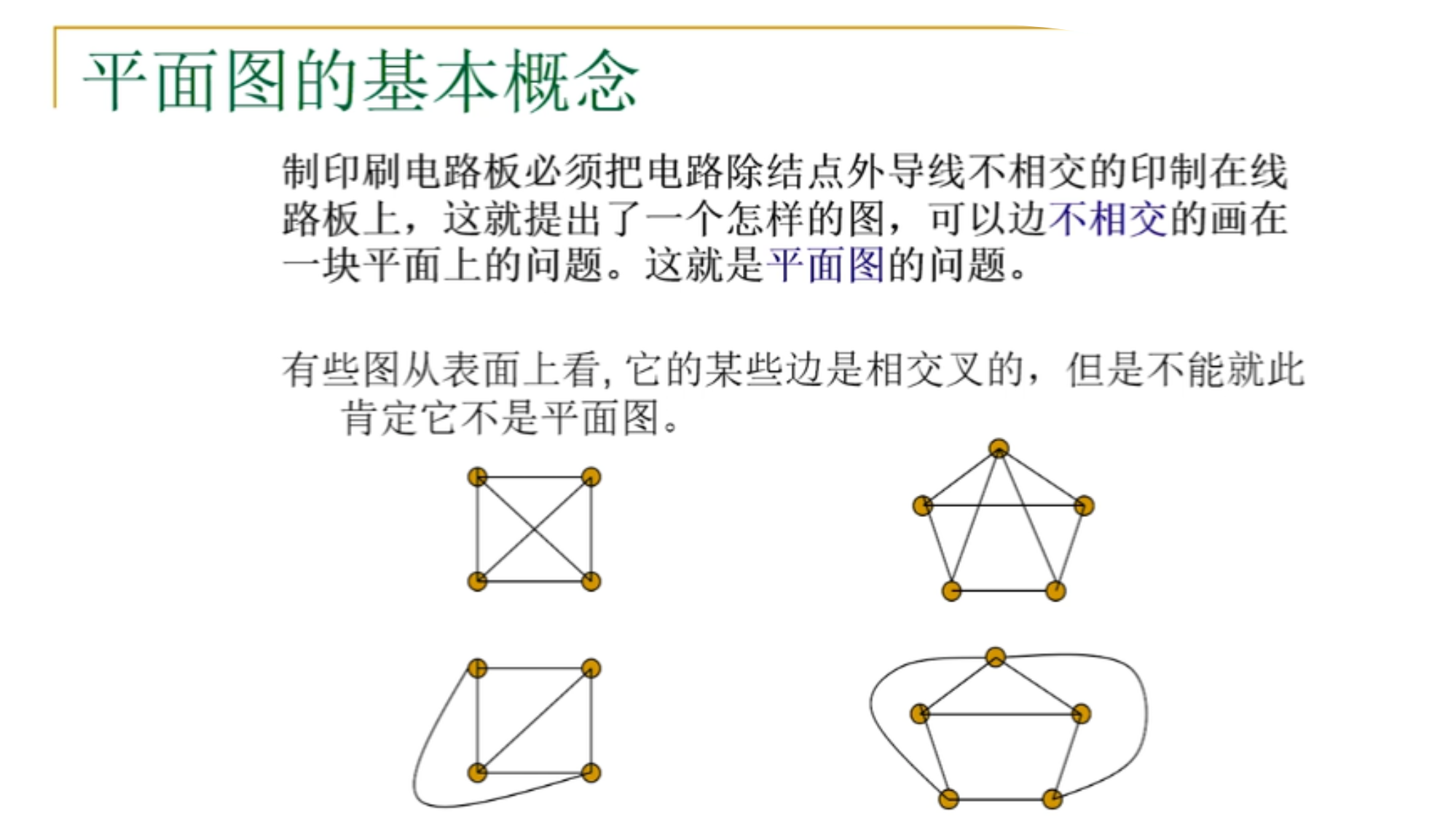
并非所有的图都能嵌入平面
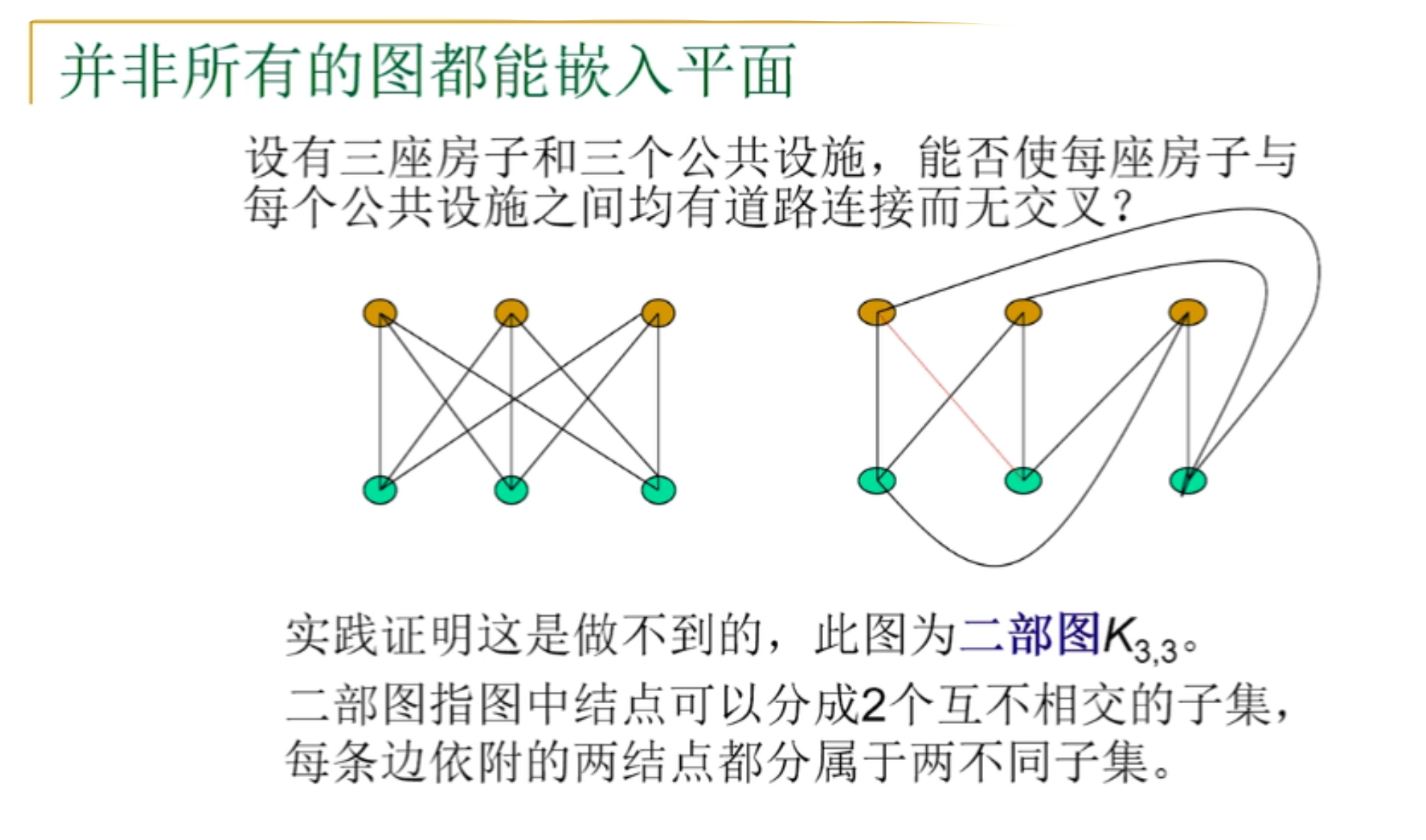
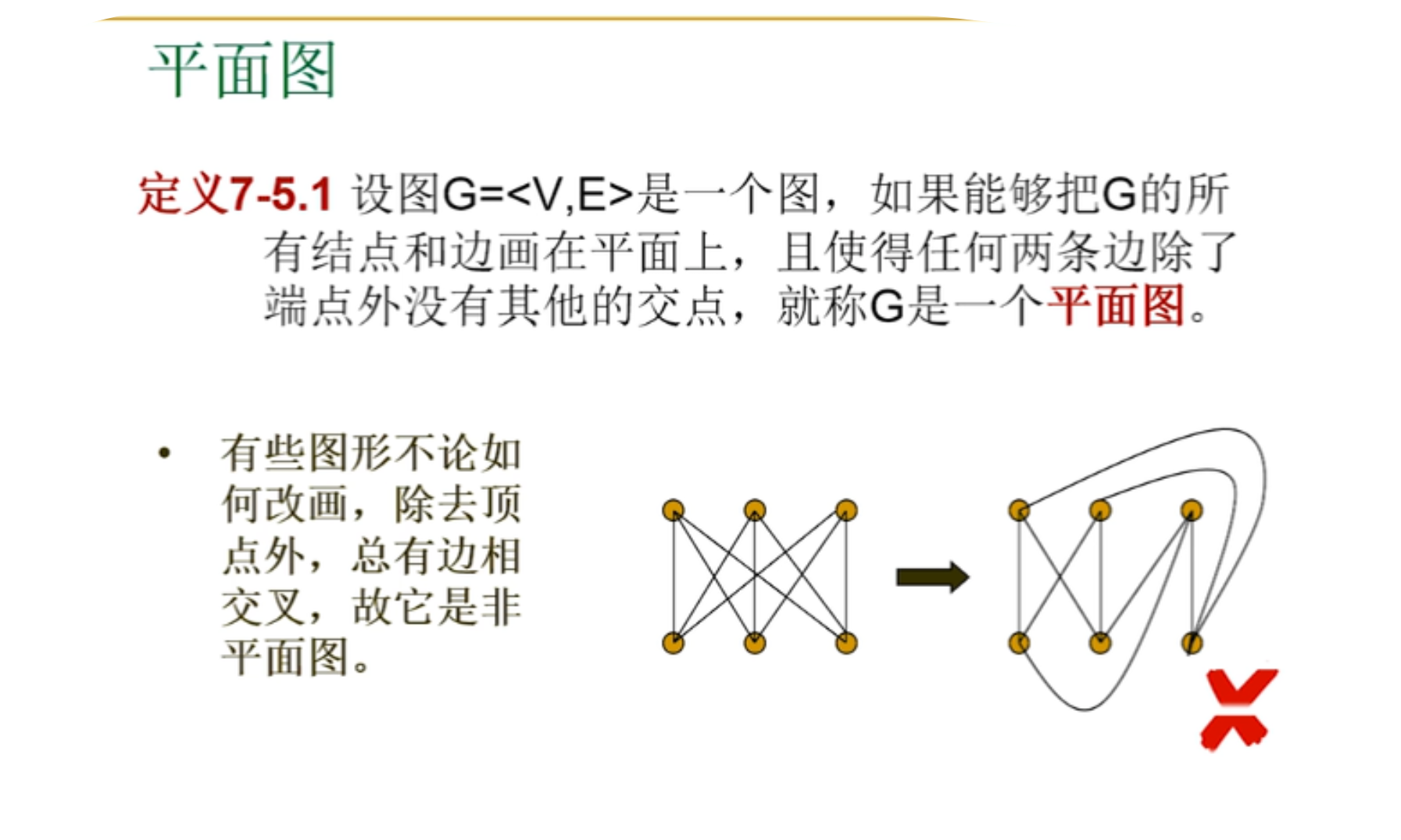
平面图的面与次数
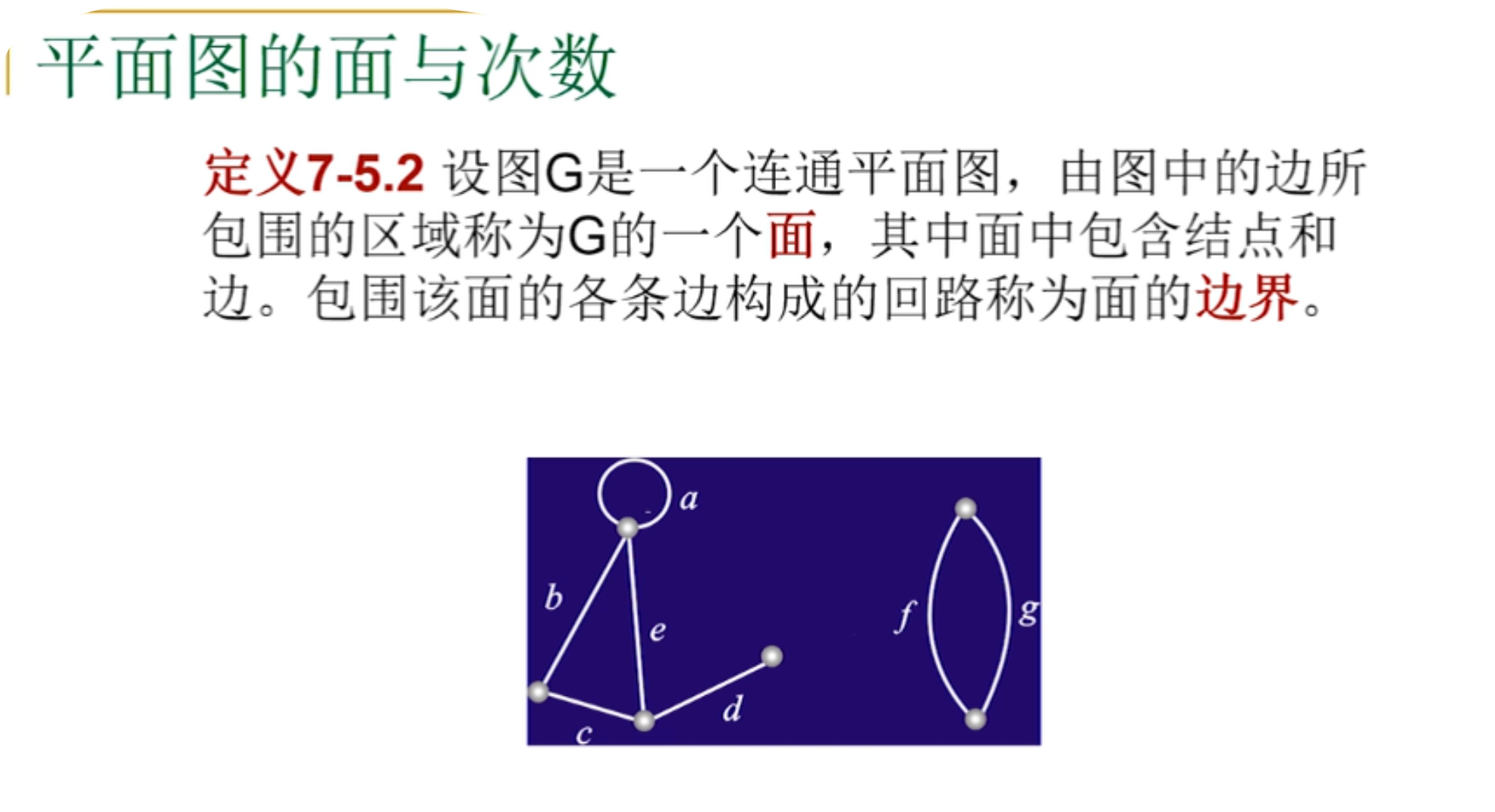

欧拉公式

欧拉公式的证明

3.平面图的判定

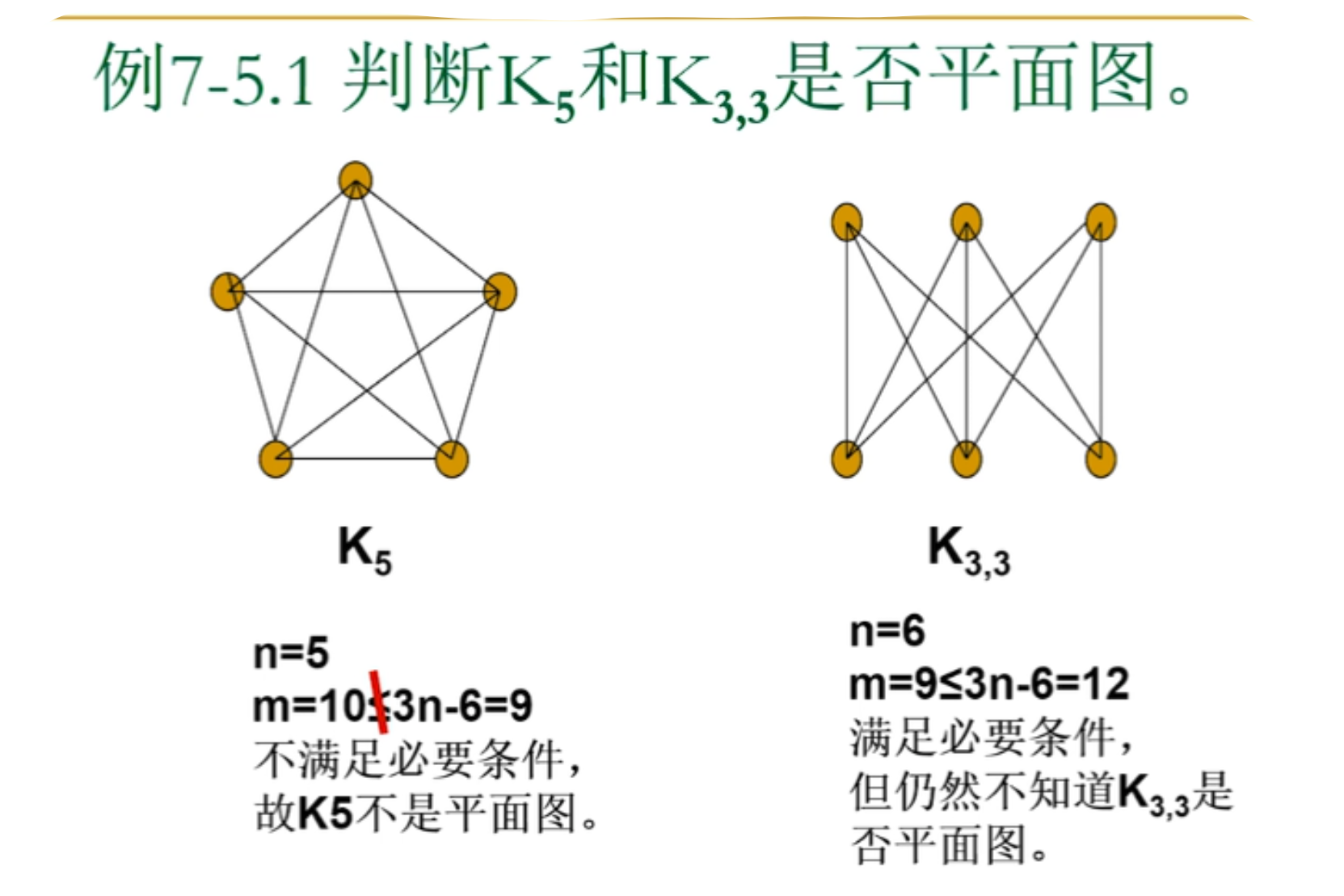
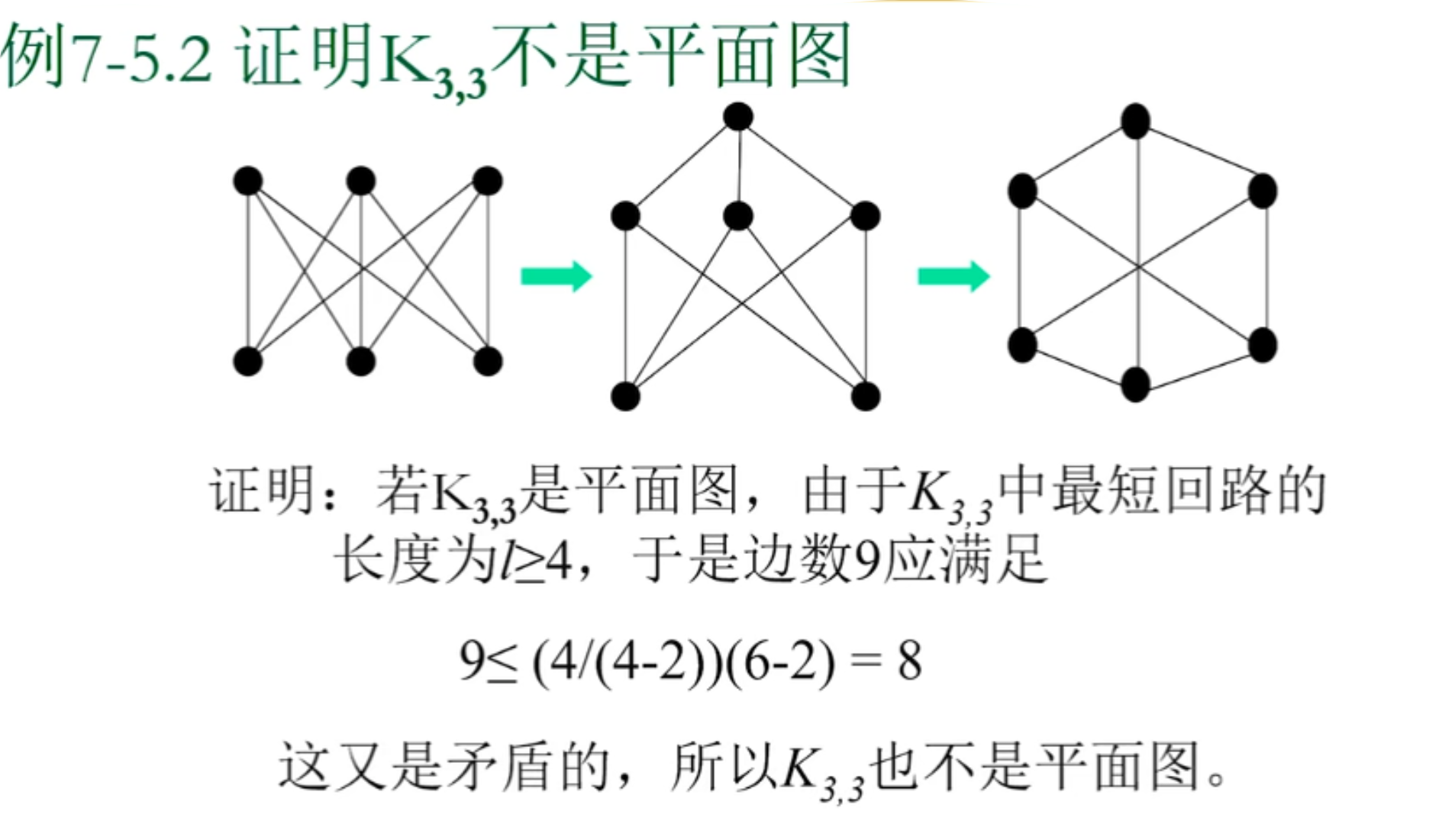
同胚
kuratowski定理
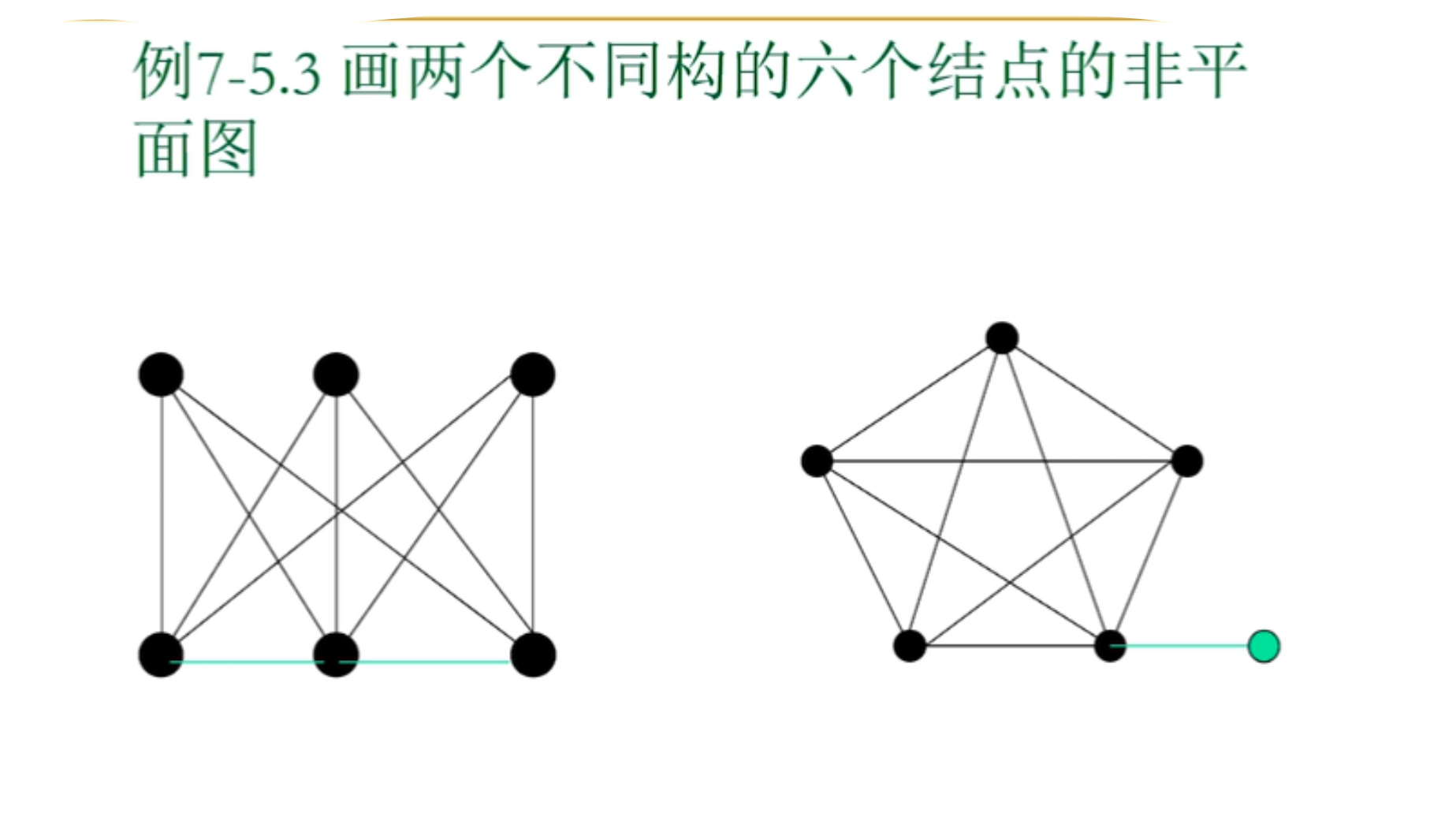 4.对偶图
4.对偶图
四色定理

平面图的着色
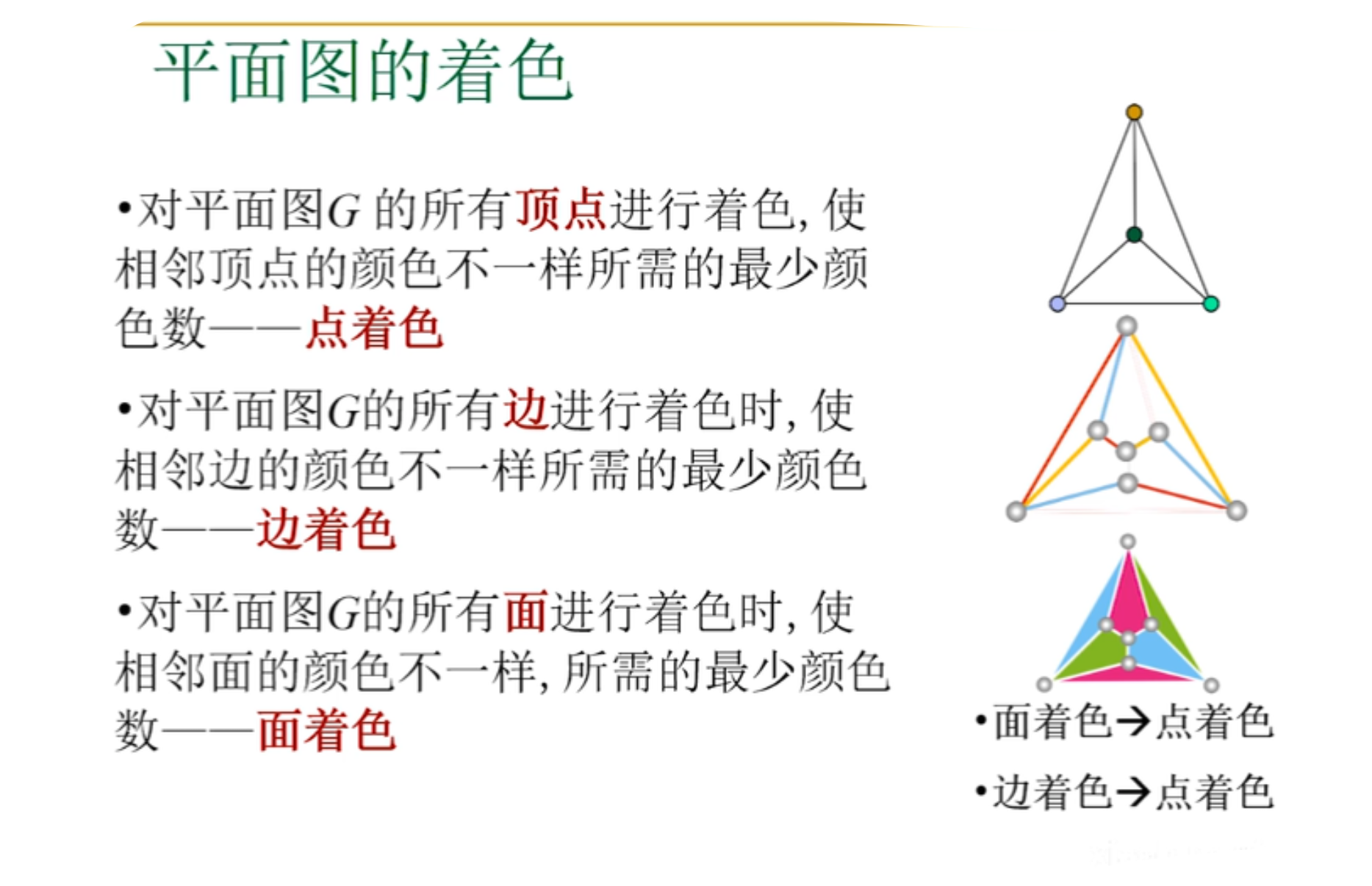
平面图的对偶图
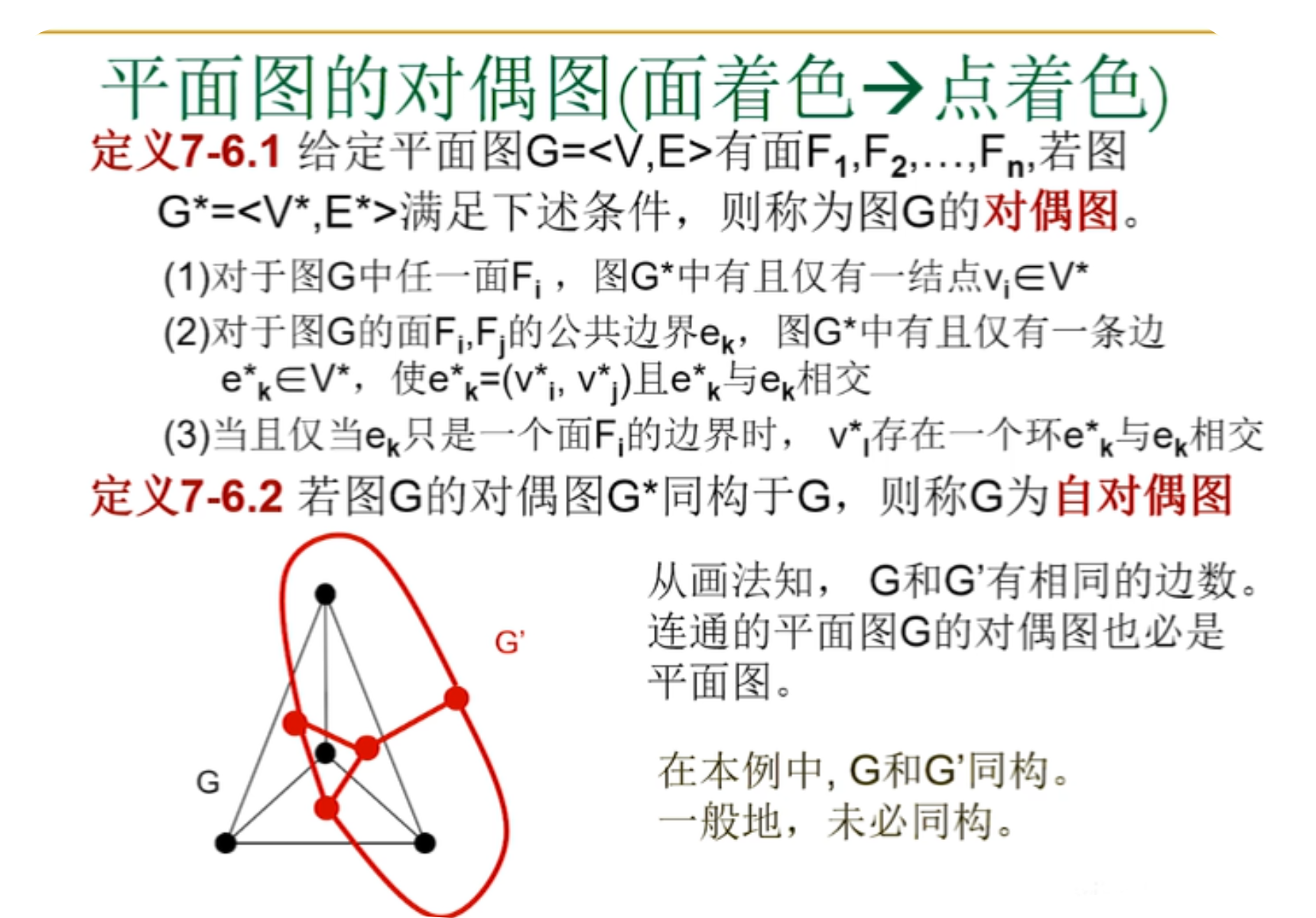
更多的对偶图示例
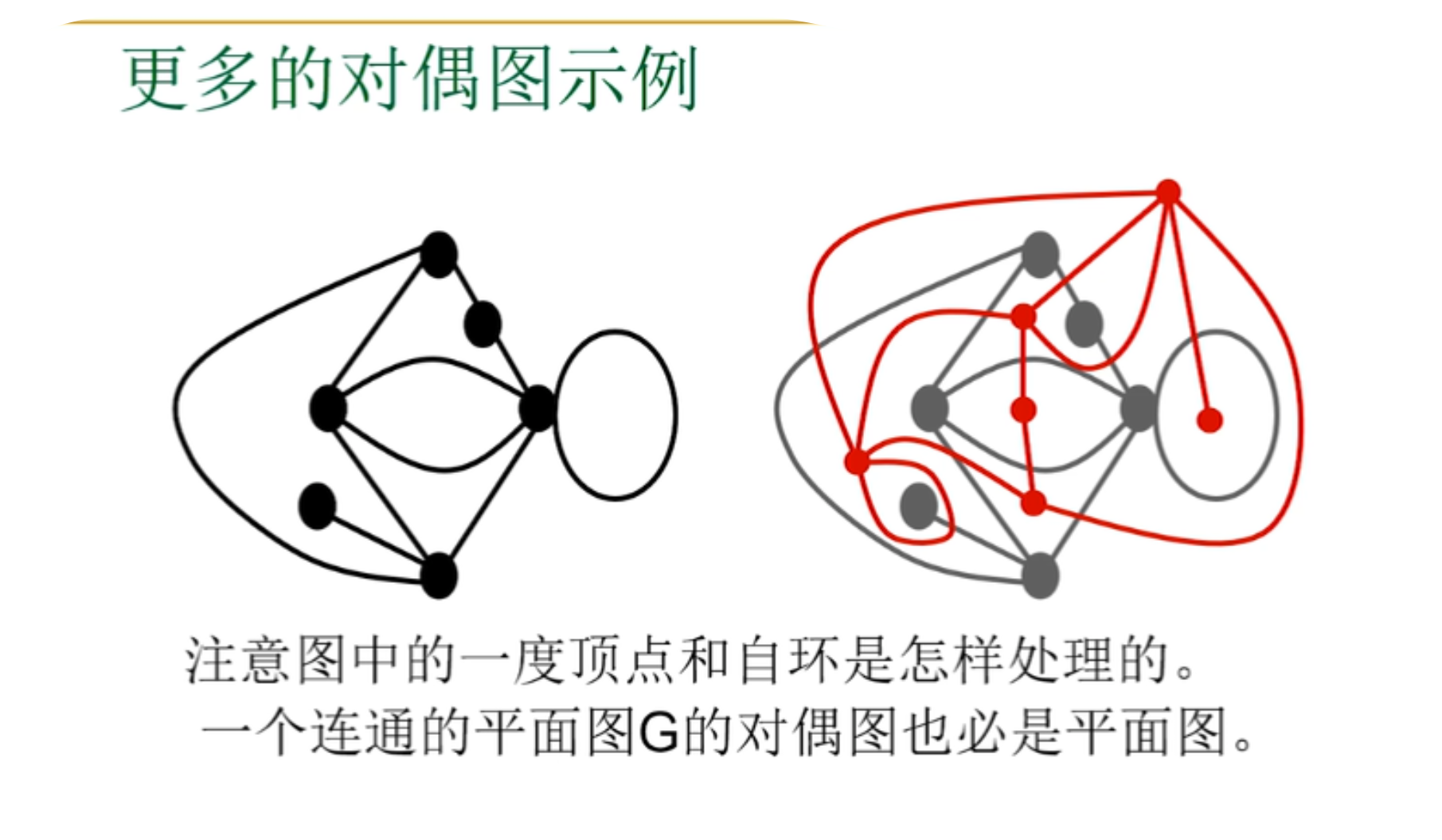
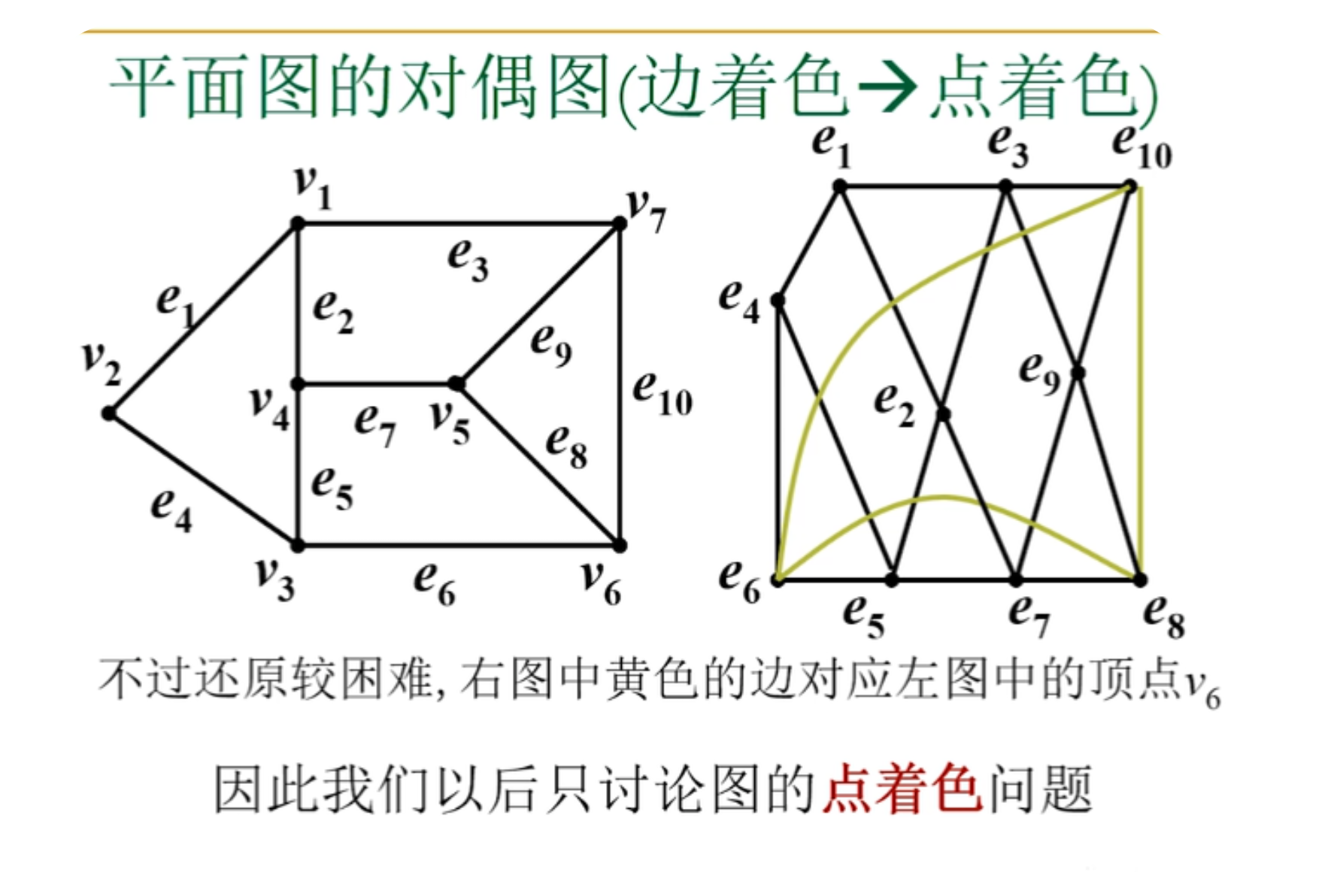
着色相关定理

平面图的五色定理

5.五色定理的证明
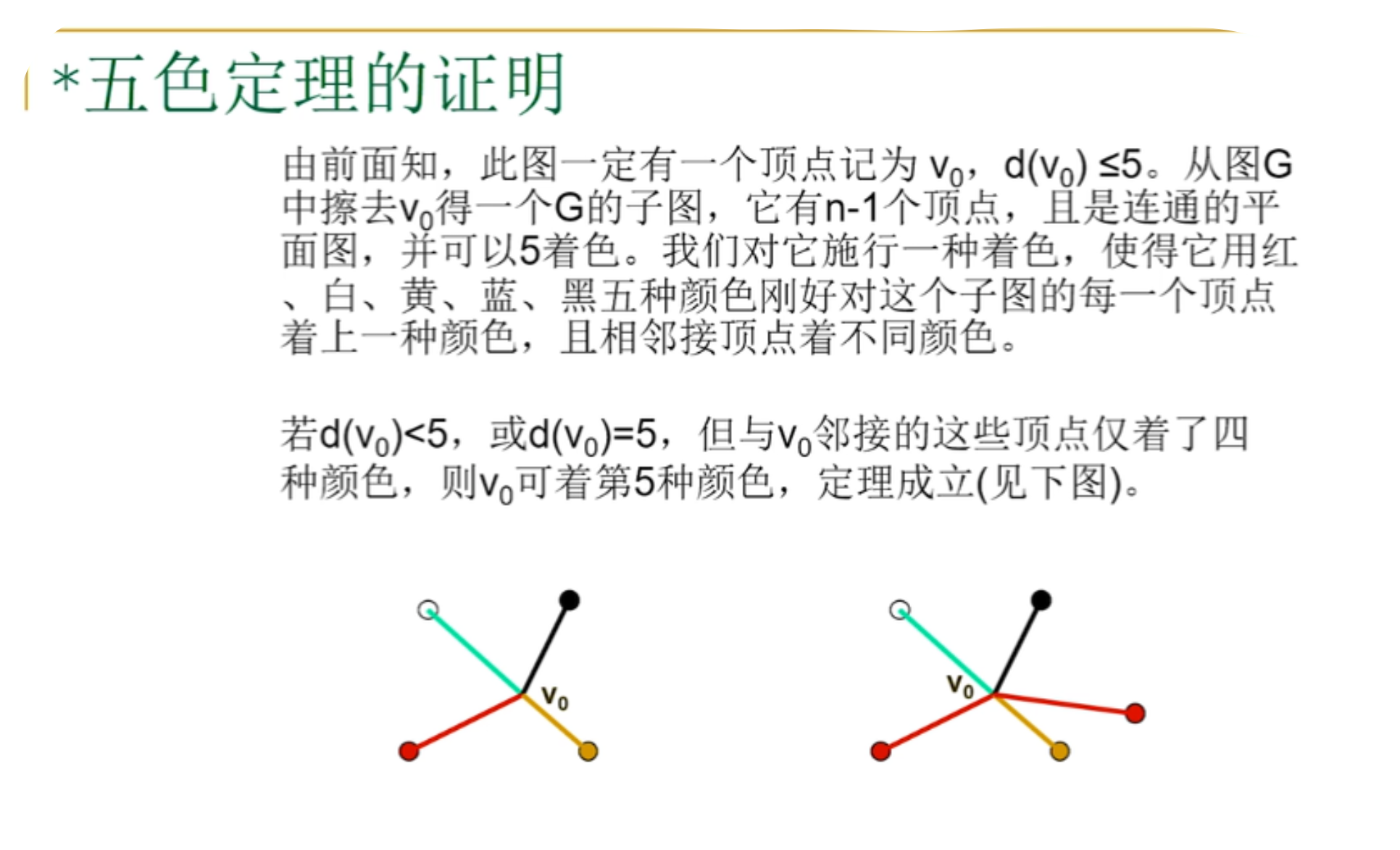
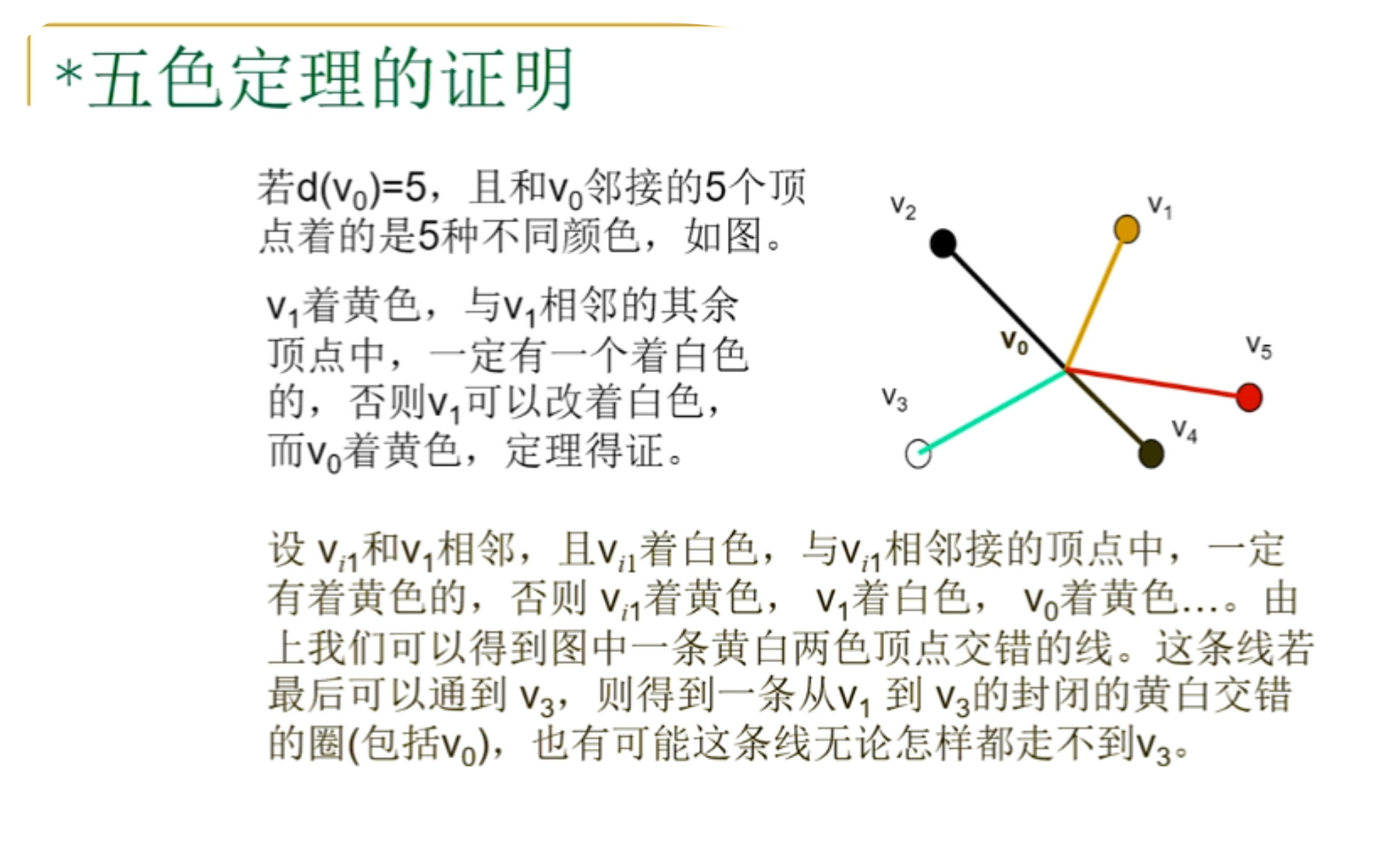
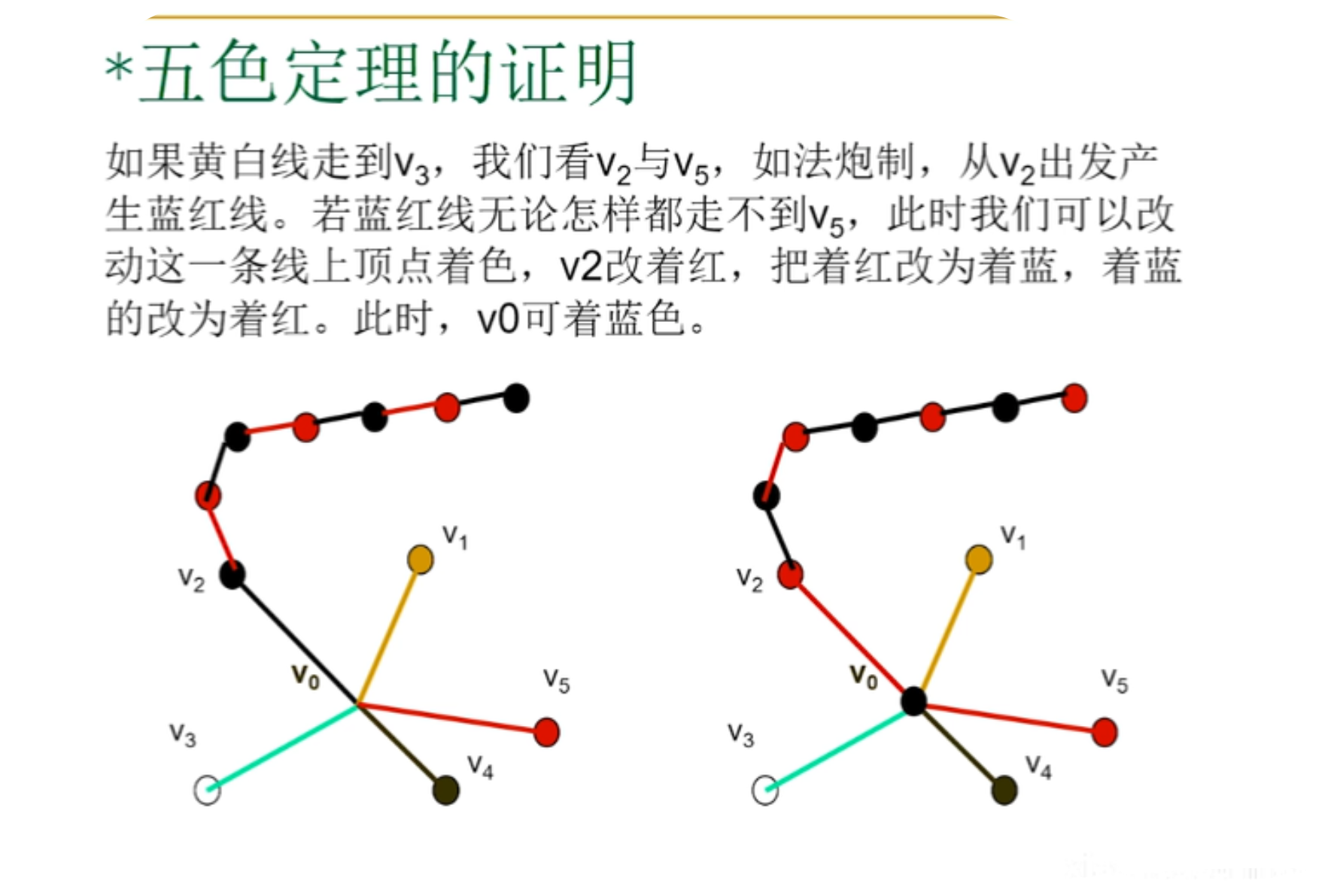
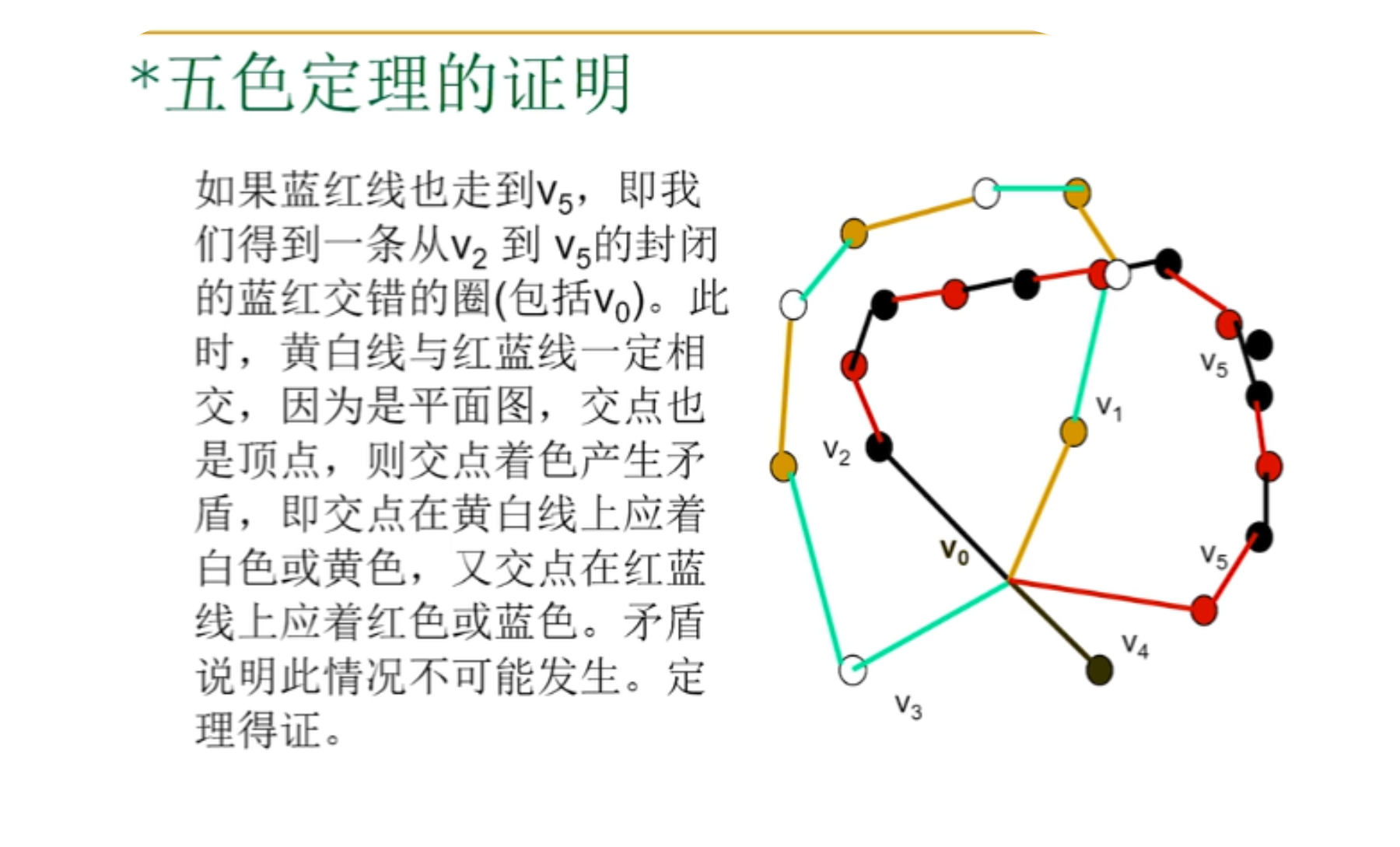
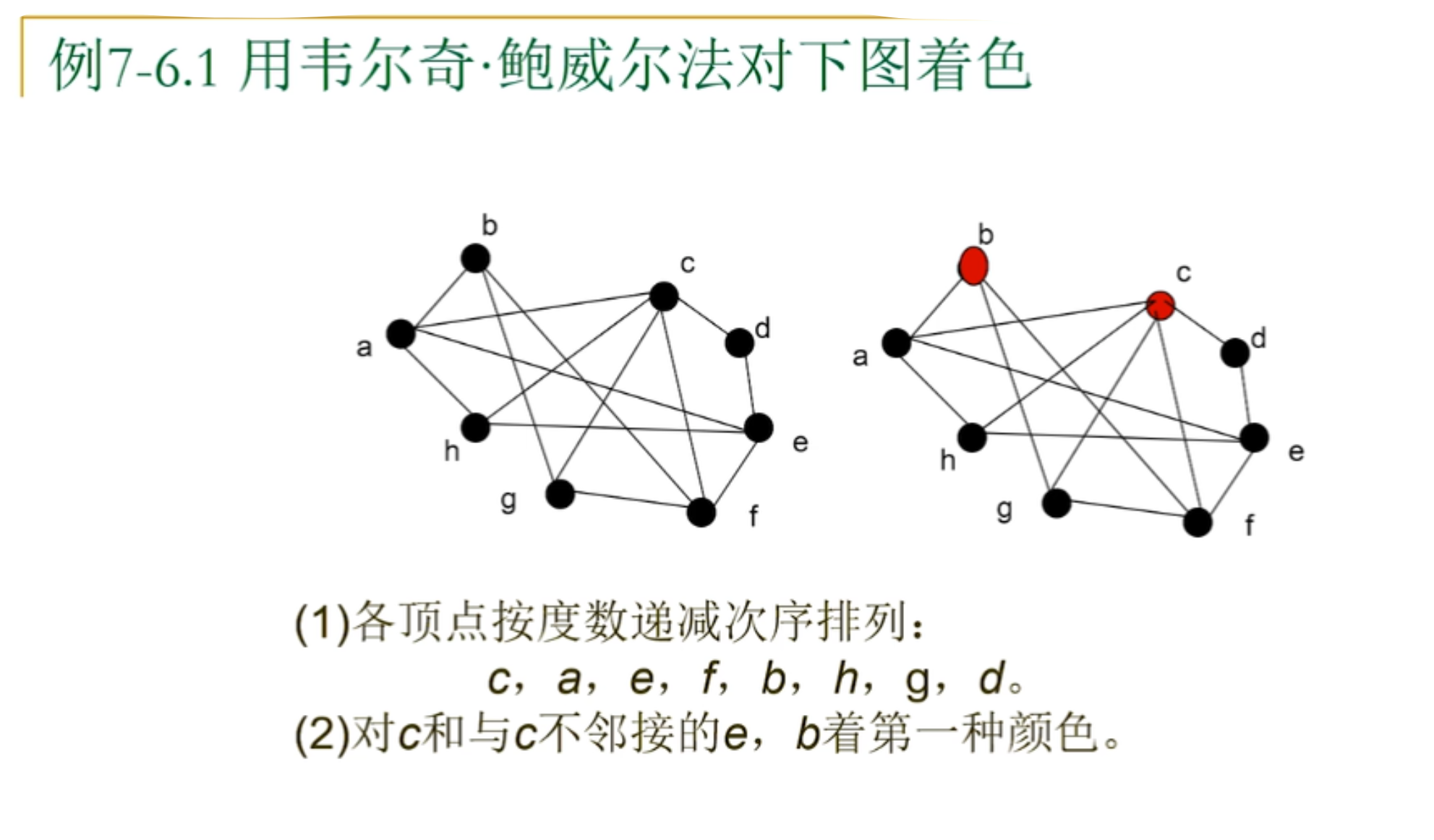
6.WelchPowell着色法

例子




![[PM]产品运营](https://img-blog.csdnimg.cn/img_convert/26a271d8cd6be477e599b603fac09760.png)













