目录
前言
一,dfs和bfs是什么
二,城市地图--图的深度优先遍历
三,最少转机--图的广度优先遍历
前言
🌼说爱你(超甜女声版) - 逗仔 - 单曲 - 网易云音乐
1月22日一个女孩加了我,她和我聊音乐,聊文学,聊人生理想。2月2日,她跟我聊起了她在山里种茶叶命苦的爷爷👺
🌼南山南 - 马頔 - 单曲 - 网易云音乐
---------------------------------------------------------------------------------------------------------------
一,dfs和bfs是什么
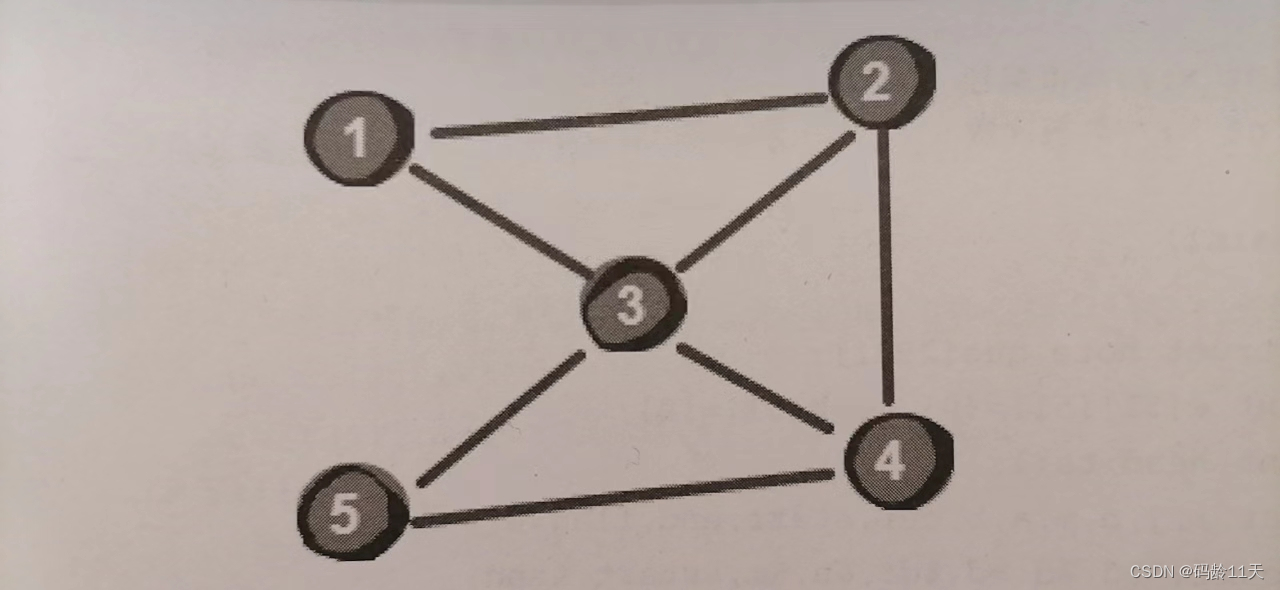
前面我么已经学过深搜和广搜,为什么叫深搜和广搜呢?这是针对图的遍历而言的,看图
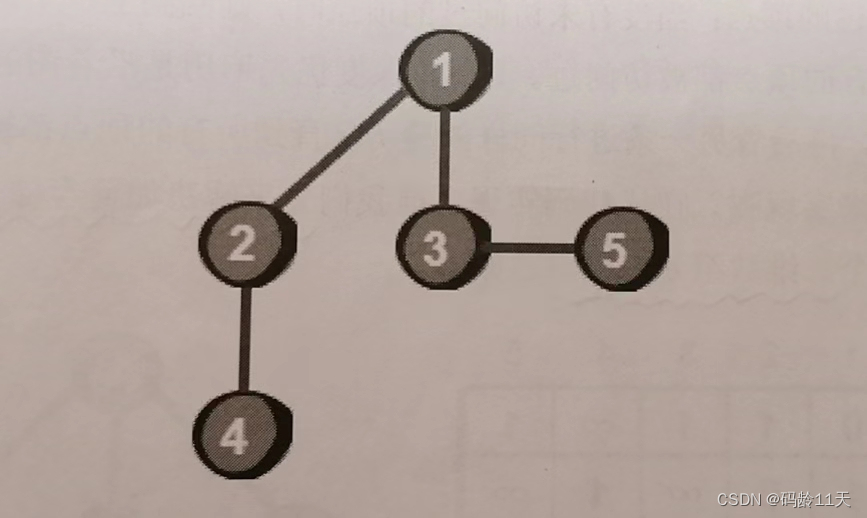
图是什么呢,图就是由一些小圆点(顶点)和连接这些小圆点的直线(边)组成的,比如上图由5个顶点(1,2,3,4,5)和5条边(1-2,1-3,1-4,2-4,3-5)组成
现在我们从1号顶点开始遍历这个图,遍历就是把图的每个顶点都访问一次,使用深搜遍历会得到下图结果(图中每个顶点上方的数字,表示该顶点第几个被访问到,叫时间戳)

深搜遍历该图的具体过程是:
1,未走过的顶点作为起始,比如1号作为顶点
2,从1号尝试访问其他未走过的顶点
3,来到2号,再从2号作为出发点继续访问其他未走过的
4,来到4号,发现没有未访问过的,返回上一步(2号顶点)
5,2号-->1号-->3号-->5号
6,至此,所有顶点都访问过了,遍历结束
深度优先的思想是,沿着图某一条分支遍历到末端,然后回溯,再沿着另一条进行同样的遍历,直到所有顶点都被访问过为止。那这一过程如何用代码实现呢?
在那之前,我们先解决如何存储一个图,我们用一个二维数组来存储,看图
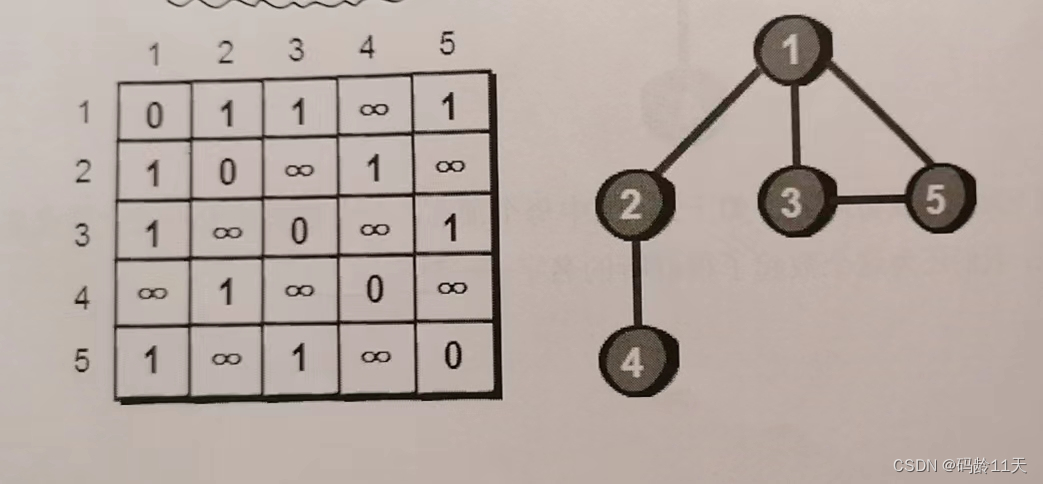
上图二维数组第 i 行第 j 列表示的是顶点 i 到顶点 j 是否有边。1 表示有边,∞ 表示没边,这里我们将自己到自己(i 到 j)设为0,此谓“图的邻接矩阵存储法”
观察发现,这个二维数组沿主对角线对称,因为该图是无向图(图的边没有方向,如果 i 到 j 有边,那么 j 到 i 也有边),例如1-5表示1号到5号有边,5号到1号也有边
接下来写个dfs实现图的遍历
void dfs(int cur) //current当前顶点编号
{
printf("%d ", cur);
sum++; //已访问顶点个数
if(sum == n) return; //遍历完毕退出
for(i = 1; i <= n; ++i) { //从1号顶点到n号依次尝试
//如果有边且未访问
if(e[cur][i] == 1) {
book[i] = 1; //标记已访问
dfs(i); //从顶点i出发继续遍历
}
}
return;
}上面代码中,变量cur(rent)存储当前顶点,二维数组e存储图的边(邻接矩阵),赋值e[cur][i]为-1记录哪些顶点被访问过,变量sum记录已访问顶点个数,变量n存储图顶点的总个数
完整代码 dfs遍历图
#include<iostream>
using namespace std;
int n, sum = 0, book[101], e[110][110];
void dfs(int cur) //current当前顶点
{
cout<<cur<<" ";
sum++;
if(sum == n) return; //遍历结束
for(int i = 1; i <= n; ++i) {
if(e[cur][i] == 1 && book[i] == 0) { //有边且未被访问
book[i] = 1;
dfs(i);
}
}
return;
}
int main()
{
int a, b; //可联通的两点
cin>>n;
for(int i = 1; i <= n; ++i) //初始化矩阵
for(int j = 1; j <= n; ++j) {
if(i == j) e[i][j]= 0; //自己到自己
else e[i][j] = 99999999; //正无穷
}
for(int i = 1; i <= n; ++i) { //标记可联通
cin>>a>>b;
e[a][b] = 1;
e[b][a] = 1; //无向图
}
book[1] = 1; //标记访问
dfs(1); //从1号顶点开始遍历
return 0;
}
5
1 2
1 3
1 5
2 4
3 5
1 2 4 3 5使用广搜遍历这个图的结果是,看图
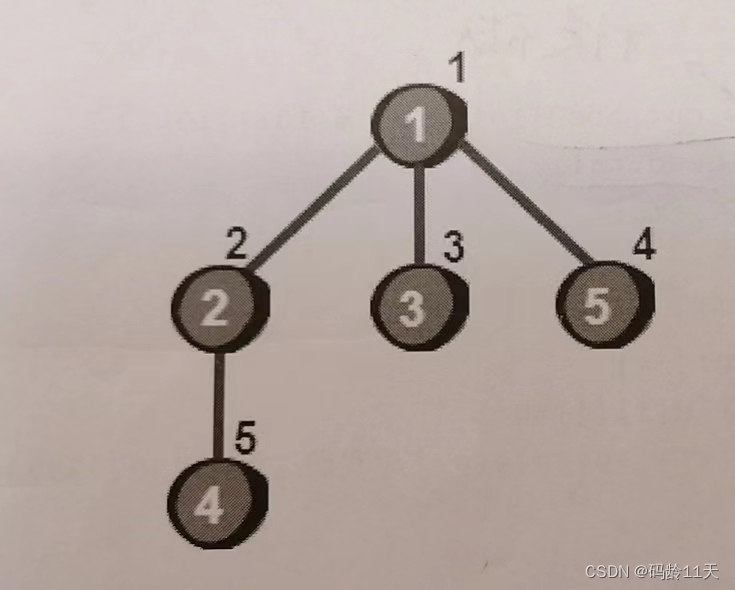
1,先以一个未访问顶点作为起始,比如1号,将1号放入队列
2,接着将与1号相邻的,未访问的顶点2号,3号,5号依次放入队列(如下图)
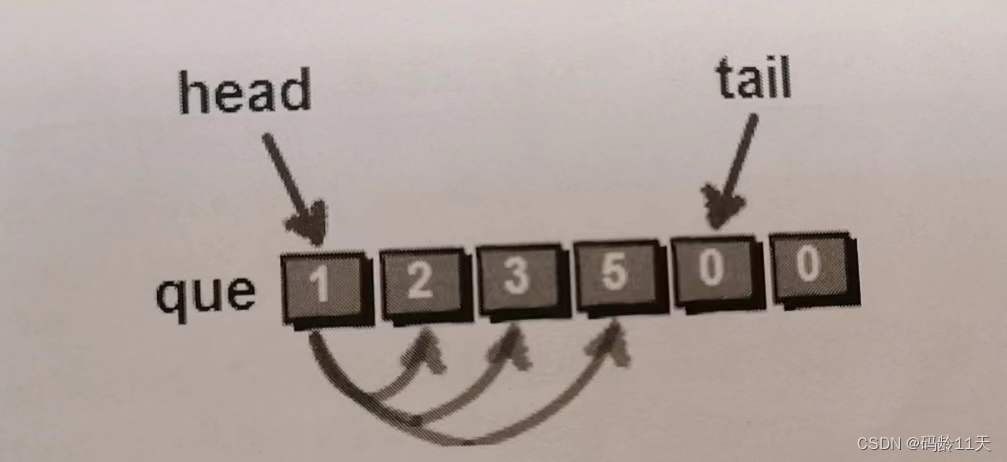
3,再将与2号相邻且未访问的4号放入队列,至此访问完毕,遍历结束(如下图)
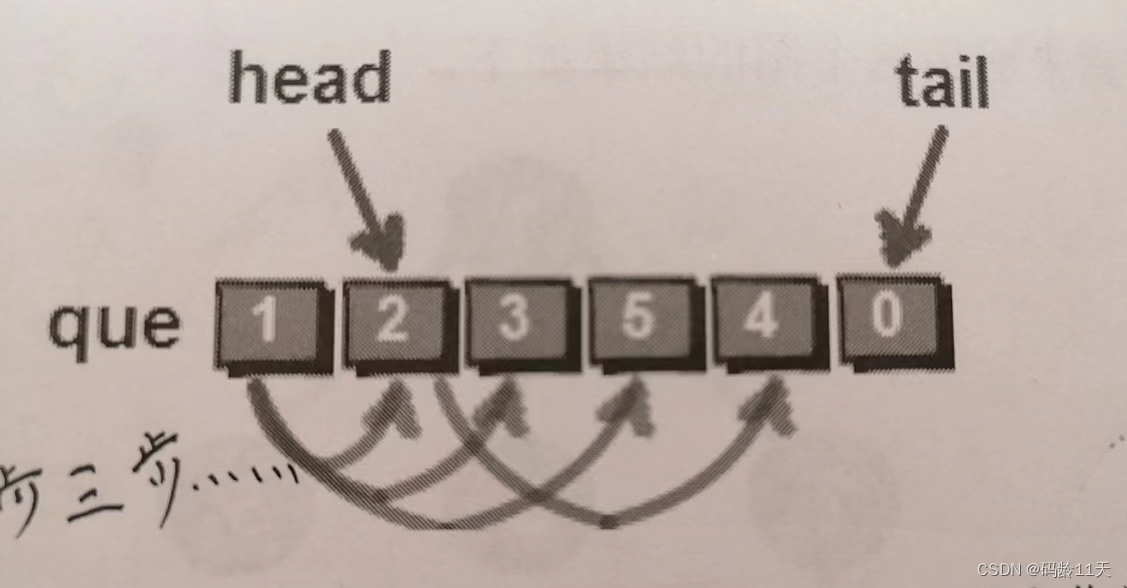
广度优先遍历的思想是
1,未访问顶点作为起始,访问所有相邻
2,接着对每个相邻顶点,再访问它们相邻未访问顶点,直至所有顶点都被访问,遍历结束
3,通俗点讲,就是访问起始顶点一步以内,两步以内直至n步以内的顶点
完整代码 bfs遍历图
#include<iostream>
using namespace std;
int main()
{
int n, a, b, cur, book[101] = {0}, e[101][101];
int que[10010], head, tail;
cin>>n;
//初始化二维矩阵
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j) {
if(i == j) e[i][j] = 0; //自己到自己
else e[i][j] = 99999999; //正无穷
}
//读入边(可联通)
for(int i = 1; i <= n; ++i) {
cin>>a>>b;
e[a][b] = 1;
e[b][a] = 1; //无向图,可逆
}
//队列初始化
head = 1; tail = 1;
//1号顶点出发,将1号加入队列
que[tail] = 1;
tail++;
book[1] = 1; //已访问
//当队列不为空
while(head < tail && tail <= n) {
cur = que[head]; //当前顶点
for(int i = 1; i <= n; ++i) { //从1~n依次尝试
//有边且未访问过
if(e[cur][i] == 1 && book[i] == 0) {
//将顶点i入队
que[tail] = i;
tail++;
book[i] = 1; //标记访问
}
if(tail > n) break;
}
head++; //一个顶点扩展结束后,head++才能继续扩展
}
for(int i = 1; i <= n; ++i) cout<<que[i]<<" ";
return 0;
}5
1 2
1 3
1 5
2 4
3 5
1 2 3 5 4使用深搜和广搜遍历图,都会得到这个图的生成树,那么什么叫生成树?生成树又有哪些作用呢?我们将在《啊哈算法》最后的博客讨论
下面来看图有什么作用,能解决什么实际问题,请看下节,城市地图↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
二,城市地图--图的深度优先遍历

寒假我(小哼)想去女朋友(小哈)家里玩,我们异地恋,住在不同城市,怎么去呢?
这时小哼想起了百度地图,百度地图一下子给出了小哼家到小哈家的最短行车方案,爱思考的小哼想知道百度地图是如何计算最短行车方案的
城市地图
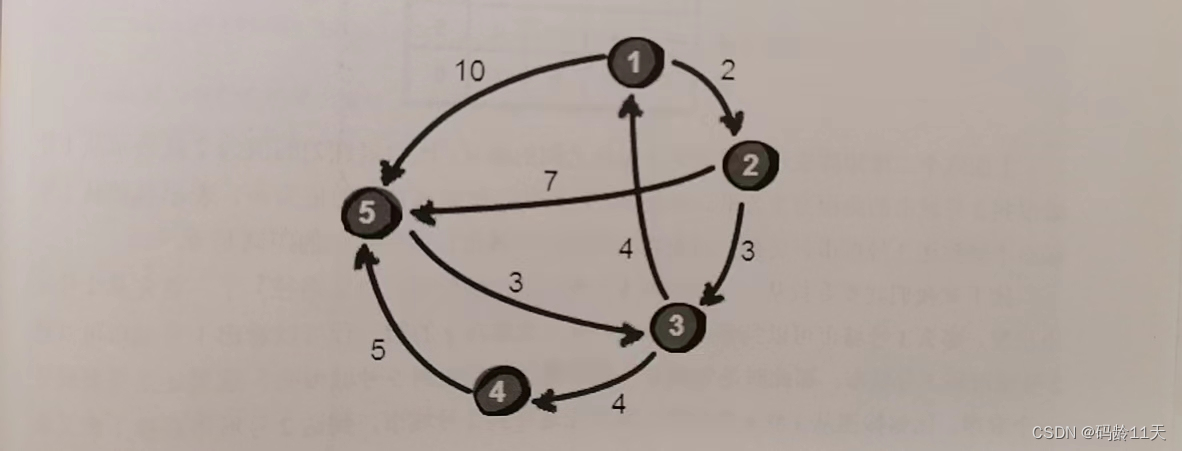
数据是这样给出的:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3第一行5表示5个城市(城市编号1~5),8表示8条公路
接下来8行,每行类似"a b c",表示有一条路可以从城市a到城市b,路程c公里
需要注意的是,这里的公路都是单行的,即有向图
小哼家在1号城市,女朋友家在5号城市,现在请算出1号城市到5号城市的最短路径(程)
为了去女朋友家玩,一定要找到最短路程!🙃
已知有5个城市,8条公路,我们用一个5 * 5矩阵(二维数组a)存储这些信息,看图:
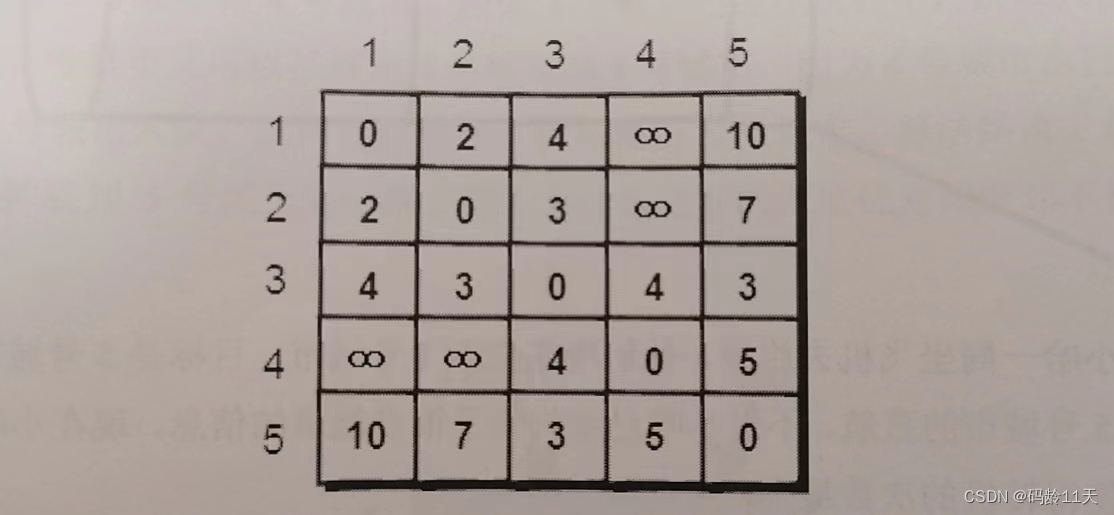
这个二维数组表示城市 i 到城市 j 之间的路程,比如a[1][2]的值为2表示1号到2号路程为2公里
∞表示无法到达,约定自己到自己的距离为0
具体实现一条1号到5号的路,再返回并逐个尝试的过程,就不讲了,我们直接开始dfs
用全局变量Min更新每次找到路径的最小值,用book[]数组记录走过的城市,用1000000000表示∞
代码
#include<cstdio> //scanf()
int Min = 99999999, book[101], a[101][101];
int n; //n个城市作为全局变量,在dfs函数中用到
void dfs(int i, int sum)
{
int j;
if(sum > Min) return; //当前路程大于当前最短路
if(i == n) { //到达目标城市
if(sum < Min) Min = sum; //更新
return;
}
for(j = 1; j <= n; ++j) { //从1号到n号城市依次尝试
//i到j有路且j未走过
if(a[i][j] != 99999999 && book[j] == 0) {
book[j] = 1; //标记
dfs(j, sum + a[i][j]); //从j城市再出发
book[j] = 0; //取消标记
}
}
return;
}
int main()
{
int i, j, m, b, c, d; //n个城市, m条公路
scanf("%d%d", &n, &m);
//初始化二维数组
for(i = 1; i <= n; ++i) //不要漏=
for(j = 1; j <= n; ++j) { //不要漏=
if(i == j) a[i][j] = 0;
else a[i][j] = 99999999;
}
//读入城市间道路
for(i = 1; i <= m; ++i) {
scanf("%d%d%d", &b, &c, &d);
a[b][c] = d;
}
//从1号城市出发
book[1] = 1;
dfs(1, 0);
printf("%d", Min);
return 0;
}5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
9现在总结一下图的概念,图就是由N个顶点和M条边组成的集合,题目中城市地图就是一个图(有向图),图中每个城市就是一个顶点,而两个城市之间的公路则是顶点的边
我们知道图分为有向图和无向图,如果给图的每条边规定一个方向,会得到有向图,其边称为有向边。在有向图中,与一个点相关联的边有出边和入边之分,而与一个有向边相关联的两个点也有始点和终点之分
边没有方向的图称为无向图,我们将上面城市地图改为无向图后:
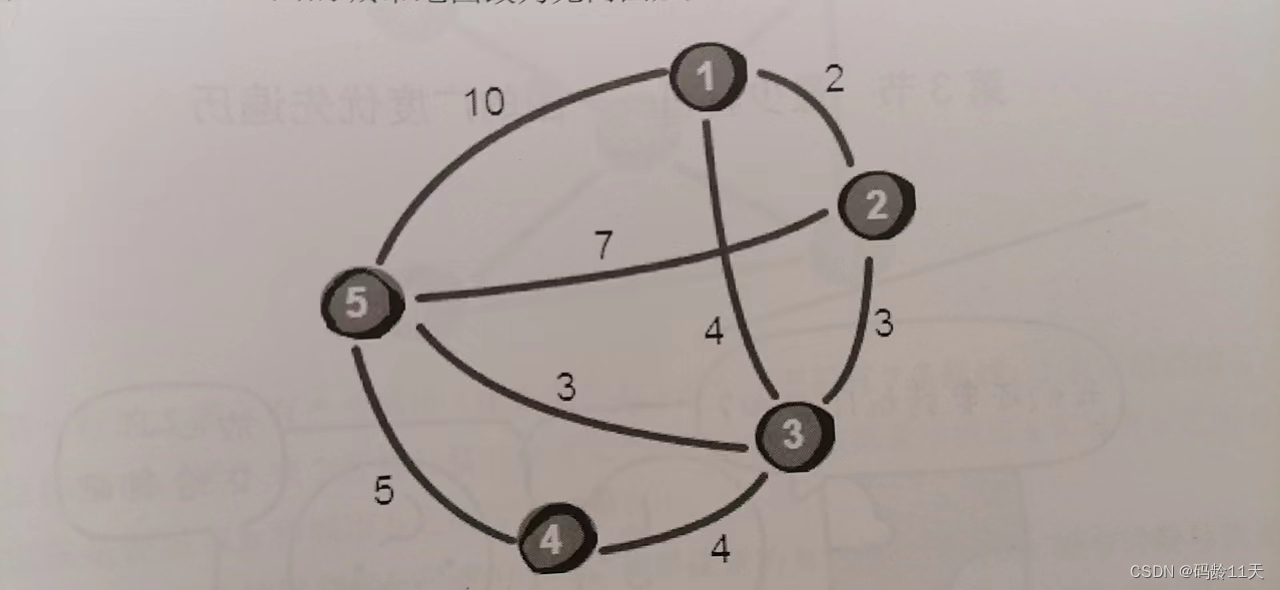
处理无向图和有向图基本一样,除了...."b c d"表示城市b和c可以互相到达,路程均为d公里,所以我们需要将a[1][2]和a[2][1]都初始化为2,因为这条公路是双行道
初始化后的数组a如下图:
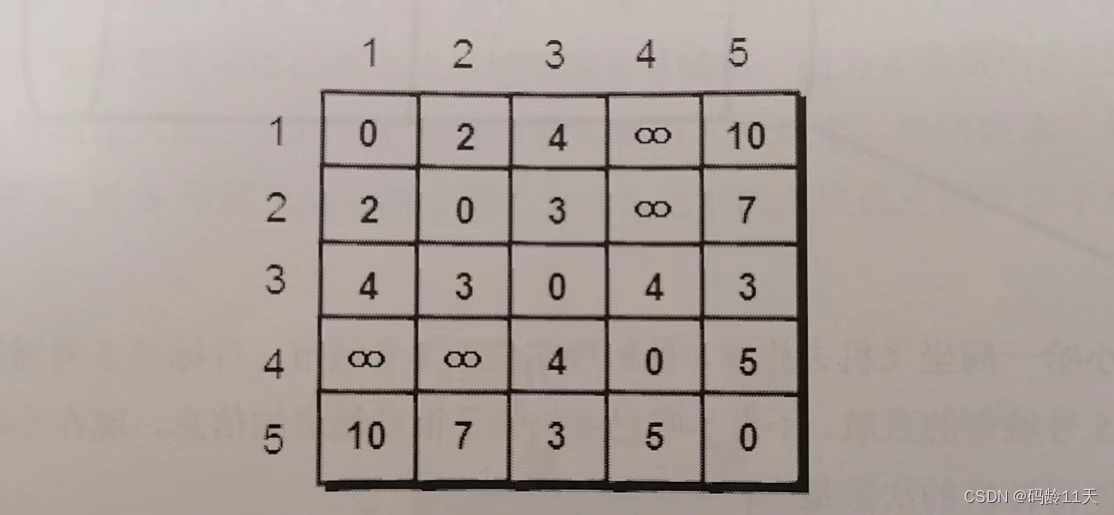
这个表是对称的(无向图的特征),我们发现此时从1号城市到5号城市的最短路径不再是1->2->5
而是1->3->5,路径长度为7
我们只需要在代码第35行(读入城市道路)加个 a[c][b] = d; 即可
#include<cstdio> //scanf()
int Min = 99999999, book[101], a[101][101];
int n; //n个城市作为全局变量,在dfs函数中用到
void dfs(int i, int sum)
{
int j;
if(sum > Min) return; //当前路程大于当前最短路
if(i == n) { //到达目标城市
if(sum < Min) Min = sum; //更新
return;
}
for(j = 1; j <= n; ++j) { //从1号到n号城市依次尝试
//i到j有路且j未走过
if(a[i][j] != 99999999 && book[j] == 0) {
book[j] = 1; //标记
dfs(j, sum + a[i][j]); //从j城市再出发
book[j] = 0; //取消标记
}
}
return;
}
int main()
{
int i, j, m, b, c, d; //n个城市, m条公路
scanf("%d%d", &n, &m);
//初始化二维数组
for(i = 1; i <= n; ++i) //不要漏=
for(j = 1; j <= n; ++j) { //不要漏=
if(i == j) a[i][j] = 0;
else a[i][j] = 99999999;
}
//读入城市间道路
for(i = 1; i <= m; ++i) {
scanf("%d%d%d", &b, &c, &d);
a[b][c] = d; a[c][b] = d;
}
//从1号城市出发
book[1] = 1;
dfs(1, 0);
printf("%d", Min);
return 0;
}
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
7本节我们采用二维数组存储这个图(顶点和边的关系),这种方法叫"邻接矩阵法"
存储图的方法还有"邻接表法".
求图上两点最短路径的方法,除了dfs, 还有bfs, Floyd, Bellman-Ford, Dijkstra等,我们将在下一章讲述
三,最少转机--图的广度优先遍历
小哼和女朋友小哈一起坐飞机去旅游,他们现在位于1号城市,目标是5号城市,可是1号城市没有到5号城市的直航,现在小哼已经收集了很多航班的信息,怎样找到一种乘坐方式,使转机次数最少呢?
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5第一行表示5个城市, 7条航线, 起点为1号城市, 目标为5号城市
接下来7行,每行"a b"表示城市a和b之间有航线,可以互相抵达(无向图)
要求转机次数最少,我们假设所有边长度都为1,接下来用bfs解决最少转机问题
步骤
一步之内
先将1号城市入队,一步之内可以到达2号或3号城市,将2号,3号入队
两步之内
2号城市可以扩展出3号和4号城市,因为3号已在队列中,只需将4号入队
3号城市可以扩展出4号和5号城市,因为4号已在队列中,只需将5号入队
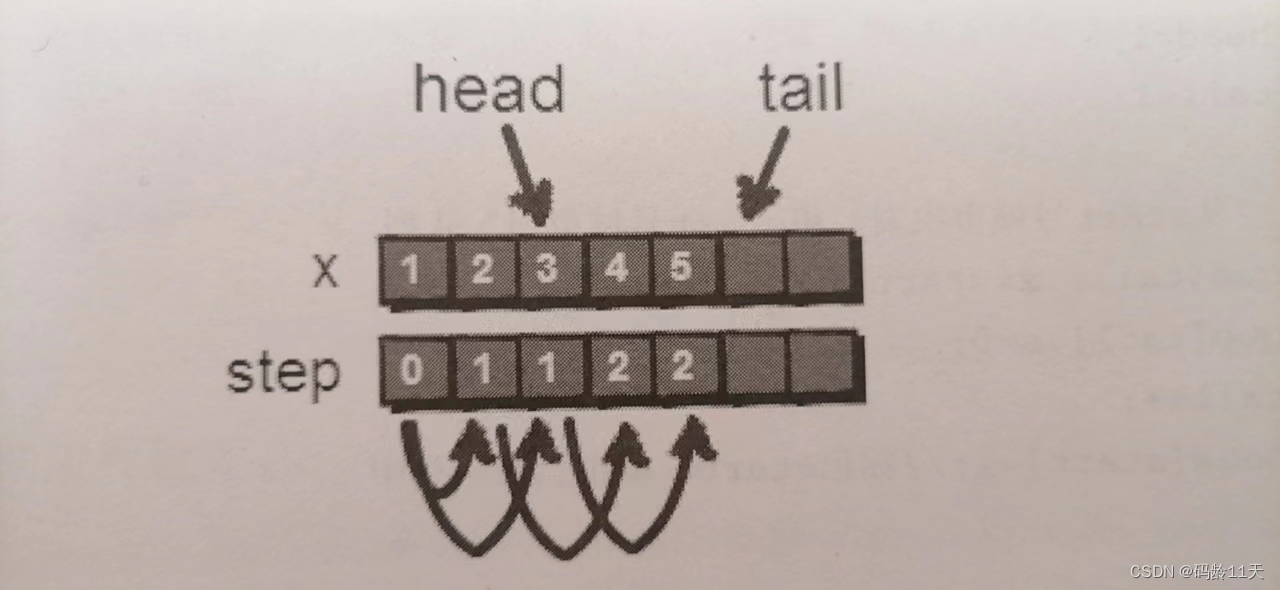
由于head(队首),是在每次对一个点完整遍历完一遍才会++,所以会出现多个点转机次数相同的情况,代表着距离出发点或n步以内
完整代码
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
2为什么最少转机次数不用dfs呢,因为广度优先搜索更适用于所有边权值相同的情况,会更快
总结
城市地图(所有边权值不同)用深搜
最少转机次数(所有边权值相同)用广搜