青大蒟蒻第一次在正式的$div2$中$Ac$了五道题，也是小蒟蒻有史以来发挥最好的一场，这场过后我的cf也许可能也要变成黄了。

A. Flip Flop Sum
题意：给定一个$a——i$数组，权值仅为1或-1，我们选择相邻两位并翻转(1变-1，-1变1），能够得到的最大和是多少，$n<=2e5$。
思路：暴力枚举所有的相邻位并翻转找最大和即可。
代码

B. The Forbidden Permutation
题意：给定一个长度为$n$排列数组$p$ , 给你长度为$m$且元素互不相同的数组$a$,一个数组是坏的当且仅当所有的$1<=i<m$满足$pos(a_i)<pos(a_{(}{i}_{+}{1}_{)})<pos(a_i)+d$，$pos(x)$表示$x$值在$a$数组的位置，现可以执行以下操作，我们可以交换$p$数组的相邻项，求执行多少次操作我们可以让$a$数组是好的，$n<=2e5,m<=2e5，a_i<=n$ 。
思路 只要破坏坏数组的条件即可，我们发现他要求的是所有的相邻位置都要满足，我们考虑有一个不满足的最小代价即可，分两种情况考虑，考虑$a(i+1)$移动到$a(i)$前面或者$a(i+1)$移动到$a(i)+d$后面，代价去最小值即可。
代码

C. Flexible String
题意：给你两个长度为$n$的字符串$a$ 、$b$,我们把价值定义为$(l,r)$对满足要求的个数$(l<=r,l>=1,r<=n)$，满足要求当且仅当$a(l,r)==b(l,r)$a字符串的l到r的子串和b字符串的l到r的子串相同。
我们定义一个$Q$堆，我们可以执行以下操作，我们可以将$a$字符串的$a_i$放到$Q$堆里，然后将$a_i$替换成任意字符$c$,$Q$堆中不同的字符串不能超过$k$种，求字符串经过若干次操作后的最大价值，题目保证字符串$a$、$b$出现的字符串种类不超过10，$k<=10,n<=2e5$。
思路：考虑对10进行二进制枚举，枚举所有的合法状态，求出对应状态的字符串的最大价值即可。时间复杂度$O(2^k\ast n)$
代码

D. Flexible String Revisit
题意：给你两个长度为$n$的二进制字符串$a$ 、$b$，字符串的取值只有$0、1$ ， 我们每一次操作可以随机选择一个下标$i$,然后把$ai$取反$(0变1，1变0)$,问把这两个字符串变相同所需的操作期望次数。

思路：考虑转化一下问题，把问题变成$ai$和$bi$相同的个数为$k$，不相同的个数可以推得为$n-k$。
然后我们把$ai$和$bi$相同的个数为$k$称为状态$k$，我们考虑由状态$k$到状态$n$的期望操作$dp[k]$次。
1.操作一次，我们选择了$ai$和$bi$相同里面的下标，由于之前是相同的，取反后变为不相同的，那么状态转移到了状态$k-1$。
2.操作一次，我们选择了$ai$和$bi$不相同里面的下标，由于取反所以不相同的下标变为了相同的下标，转移到了状态$k+1$。
可以推出式子为：$$dp[k]=1+k/n\ast dp[k-1]+(n-k)/n\ast dp[k+1]$$
观察一下这个式子，我们发现式子中出线了$dp[k-1]和dp[k+1]$，这样的式子是没法求出答案的。

我们考虑转化角度，我们考虑从状态$k$到状态$k+1$所需的期望操作$dp[k]$次，答案就为$dp[k]$从$m$到$n-1$的和,原因是$m$变到$n$，我们先花费$dp[m]$变成$m+1$,再花费$dp[m+1]$变成$m+2$…以此类推花费$dp[n-1]$变到$n$。
考虑状态转移。
1.操作一次，我们选择了$ai$和$bi$不相同里面的下标，由于取反所以不相同的下标变为了相同的下标，转移到了状态$k+1$，操作次数为1。
2…操作一次，我们选择了$ai$和$bi$相同里面的下标，由于之前是相同的，取反后变为不相同的，那么状态转移到了状态$k-1$，我们从状态$k-1$变到$k+1$需要经历$dp[k-1]$次操作变成状态$k$，再经历$dp[k]$次操作变成状态$k+1$，操作次数为$1+dp[k-1]+dp[k]$。
式子就变为：$$dp[k]=(n-k)/n+k/n\ast (1+dp[k-1]+dp[k])$$
考虑化简，化简过程如下：

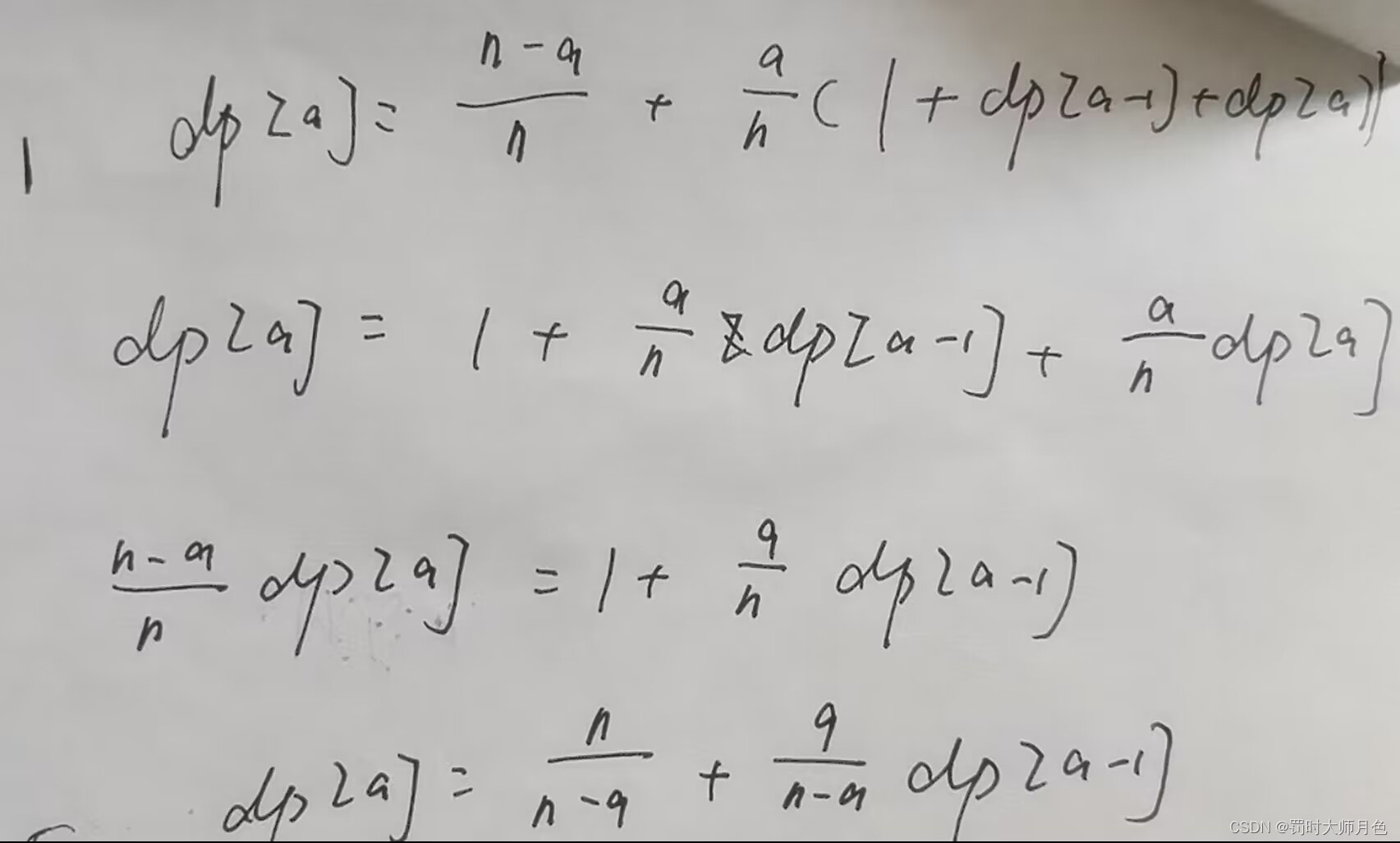
最后式子变为$$dp[k]=n/(n-k)+k/(n-k)\ast dp[k-1]$$
转移这个式子即可，初始值$dp[0]=1$,因为由0转移到1一定是一次，因为相同的为空，只能从不相同的选，然后求$m-(n-1)$的$dp[k]$和即可。
代码

E. The Tree Has Fallen!
题意：给你一棵大小为$n$的树，每个点有权值$ai$，有$q$次询问，每次询问问以$r$为根，在$u$子树中选若干个点使得这些点的权值异或和最大，输出这个最大异或和。
思路：考虑离线，我们把询问都变成问$r$为根,$u$子树的最大异或和的形式，然后我们两遍$dfs$，第一遍$dfs$维护以1为根的$sz[u]$的最大异或和(线性基），第二遍$dfs$类似换根$dp$的思路维护以$u$为根的其他节点子树的最大异或和(线性基) ，然后离线地处理所有询问。
原理：两个子树为根的所有维护的子树信息，唯一不同的地方是两个子树之间的路径信息(有根树的方向不一样),然后我们可以考虑先维护1子树的信息，然后用$dfs$特性(可以维护路过的路径信息)去解决问题即可。
往后会更新原理的图文方便理解，线性基合并是基本内容，暂且不在这里细讲。
代码