一、问题

二、分析

这道题属于一个背包问题，但是这道题中有一个很神奇的条件。就是我们想要购买某个物品的附件的话，前提是我们要购买这个物品的主件。

因此，我们可以将这道题画成下面这张图的样子：

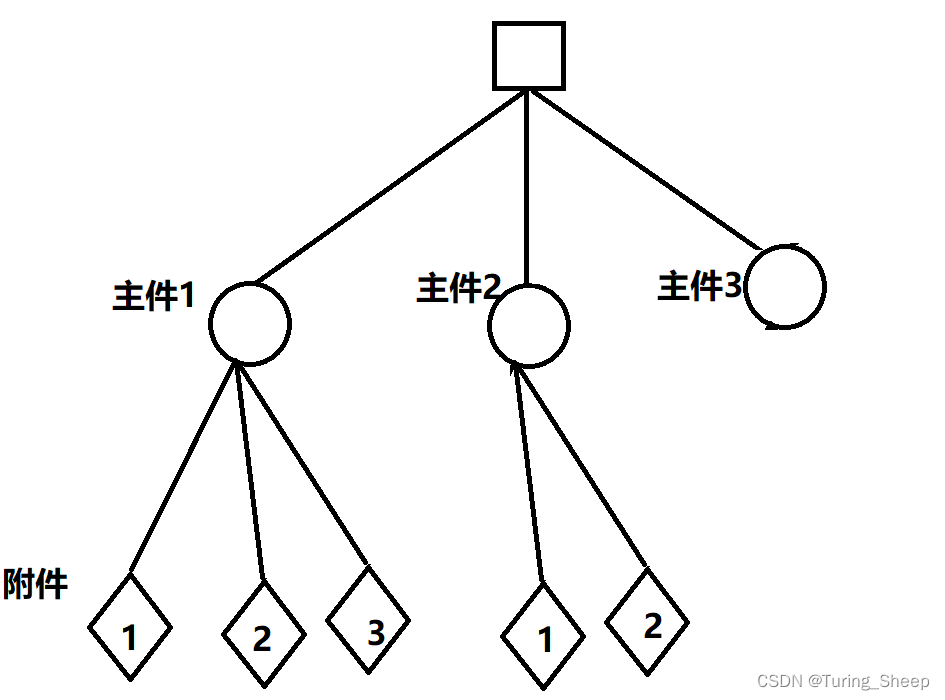
那么上面这个图中我们这个题就可以转化为，想要选择子节点，就必须选择父节点。

那么还能怎么继续转化呢？

我们继续看下面的图：

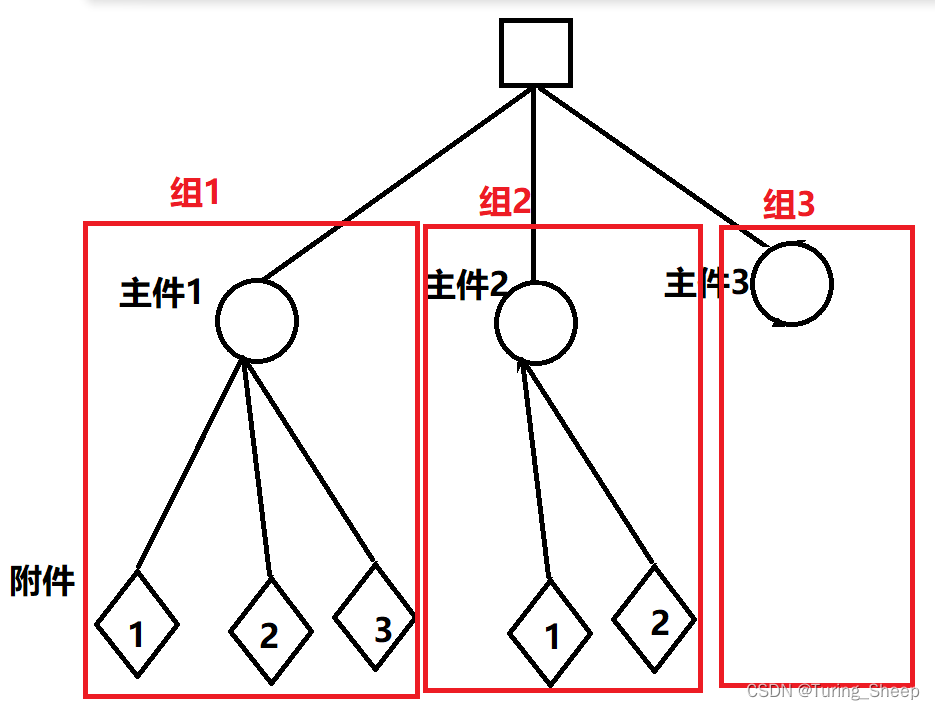
按照上面图的意思，我们可以将其转化为一个分组背包问题。

那么每一组里面的物品又是什么呢？

我们拿出其中一组来分析：

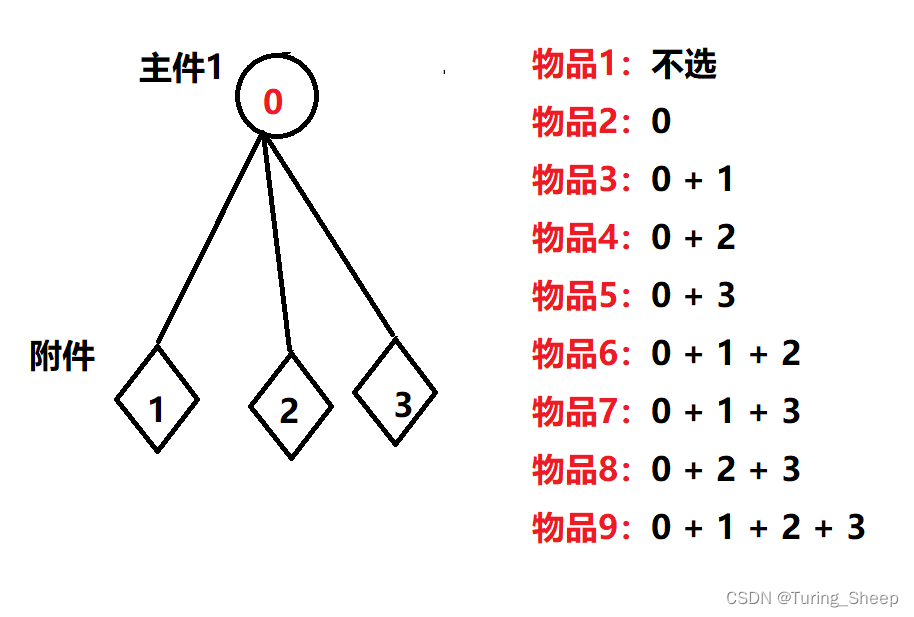
从上图中可以看出，我们将每一种可能的选择都看成组中的一个物品。

那么怎么表示每种方式呢？

其实表示的方式我们之前用过-----二进制

由于这道题的题干中明确表示，一个物品的附件不超过三个，所以一共的选择最多8种，因此时间复杂度并不高。

那么分析到这里其实这道题就很清晰了。

按照主件分成若干组，每一种附件的选择都看成组内的一种选择。

三、代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N = 32010, M = 60;
pii master[M];
vector<pii> servent[M];
int f[M][N];
int m, n;

int main()
{
	cin >> m >> n;
	for(int i = 1; i <= n; i ++ )
	{
		int v, p, q;
		cin >> v >> p >> q;
		p *= v;
		if(!q)master[i] = {v, p};
		else servent[q].push_back({v, p});
	}

	for(int i = 1; i <= n; i ++ )
	{
		for(int j = 0; j <= m; j ++ )
		{
			f[i][j] = f[i - 1][j];
			for(int k = 0; k < 1 << servent[i].size(); k ++ )
			{
				int v = master[i].first, w = master[i].second;
				for(int u = 0; u < servent[i].size(); u ++ )
				{
					if( k >> u & 1)
					{
						v += servent[i][u].first;
						w += servent[i][u].second;
					}
				}
				if( j >= v)
				{
					f[i][j] = max(f[i][j], f[i - 1][j - v] + w);
				}
			}
		}
	}
	cout << f[n][m] << endl;
	return 0;
}