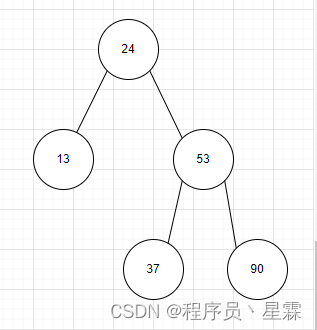
1、在下图所示的平衡二叉树中插入关键字48后得到一棵新平衡二叉树，在新平衡二叉树中，关键字37所在结点的左、右子结点中保存的关键字分别是（）。

• A：13,48
• B：24,48
• C：24,53
• D：24,90

解析

插入48后，该二叉树根结点的平衡因子由-1变为-2，失去平衡，需要进行两次旋转（先右旋后左旋）操作。

答案：C

2、若平衡二叉树的高度为6，且所有非叶子结点的平衡因子均为1，则该平衡二叉树的结点总数为（）。

• A：12
• B：20
• C：32
• D：33

解析

所有非叶结点的平衡因子均为1，即平衡二叉树满足平衡的最少结点情况，如下图所示。对于高度为n、左右子树的高度分别为n-1和n-2、所有非叶结点的平衡因子均为1的平衡二叉树，计算总结点数的公式为$C_n$=$C_{n-1}$+$C_{n-2}$+1，$C_1$=1，$C_2$=2,$C_3$=2+1+1=4，可推出$C_6$=20。

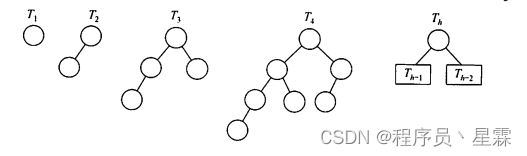
画图法：先画出$T_1$和$T_2$；然后新建一个根结点，连接$T_2$、$T_1$构成$T_3$；新建一个根结点，连接$T_3$、$T_2$构成$T_4$…直到画出$T_6$，可知$T_6$的结点数为20。

答案：B

3、若将关键字1,2,3,4,5,6,7依次插入初始为空的平衡二叉树T，则T中平衡因子为0的分支结点的个数是（）。

• A：0
• B：1
• C：2
• D：3

解析

利用7个关键字构建平衡二叉树T，平衡因子为0的分支结点个数为3，构建的平衡二叉树及构造与调整过程如下图所示。

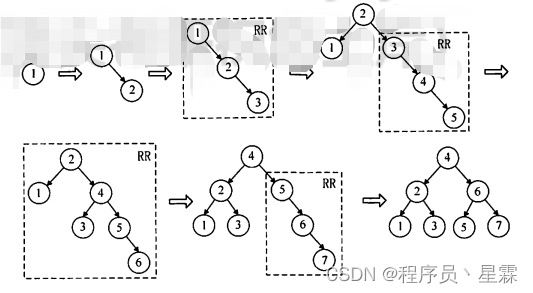
答案：D

4、现有一棵无重复关键字的平衡二叉树（AVL），对其进行中序遍历可得到一个降序序列。下列关于该平衡二叉树的叙述中，正确的是（）。

• A：根结点的度一定为2
• B：树中最小元素一定是叶结点
• C：最后插入的元素一定是叶结点
• D：树中最大元素一定是无左子树

解析

只有两个结点的平衡二叉树的根结点的度为1，A错误。

中序遍历后可以得到一个降序序列，树中最小元素一定无左子树（可能有右子树），因此不一定是叶结点，B错误。

最后插入的结点可能会导致平衡调整，而不一定是叶结点，C错误。

答案：D

5、在任意一棵非空平衡二叉树（AVL树）$T_1$中，删除某结点v之后形成平衡二叉树$T_2$，再将v插入$T_2$形成平衡二叉树$T_3$。下列关于$T_1$与$T_3$的叙述中，正确的是（）。

Ⅰ、若v是$T_1$的叶结点，则$T_1$与$T_3$可能不相同
Ⅱ、若v不是$T_1$的叶结点，则$T_1$与$T_3$一定不相同
Ⅲ、若v不是$T_1$的叶结点，则$T_1$与$T_3$一定相同

• A：仅Ⅰ
• B：仅Ⅱ
• C：仅Ⅰ、Ⅱ
• D：仅Ⅰ、Ⅲ

解析

在非空平衡二叉树中插入结点，在失去平衡调整前，一定插入在叶结点的位置。

若删除的是$T_1$的叶结点，则删除后平衡二叉树可能不会失去平衡，即不会发生调整，再插入此结点得到的二叉平衡树$T_1$与$T_3$相同；若删除后平衡二叉树失去平衡而发生调整，再插入结点得到的二叉平衡树$T_3$与$T_1$可能不同。Ⅰ正确。

对于比较绝对的说法Ⅱ和Ⅲ，通常只需举出反例即可。

例如，如下图所示，删除结点0，平衡二叉树失衡调整，再插入结点0后，平衡二叉树和以前不同。

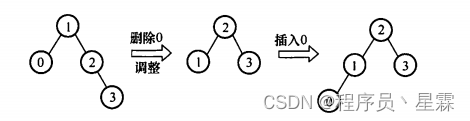
若删除的是$T_1$的非叶结点，且删除和插入操作均没有导致平衡二叉树的调整，则该结点从非叶结点变成了叶结点，$T_1$与$T_3$显然不同。例如，如下图所示，删除结点2，用有孩子结点3填补，再插入结点2，平衡二叉树和以前不同。

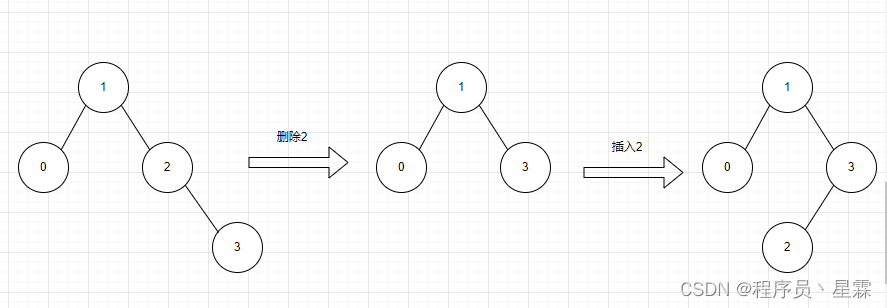
若删除的是$T_1$的非叶结点，且删除和插入操作后导致了平衡二叉树的调整，则该结点有可能通过旋转后继续变成非叶结点，$T_1$与$T_3$相同。例如，如下图所示，删除结点2，用右孩子结点3填补，再插入结点2，平衡二叉树失衡调整，调整后的平衡二叉树和以前相同。

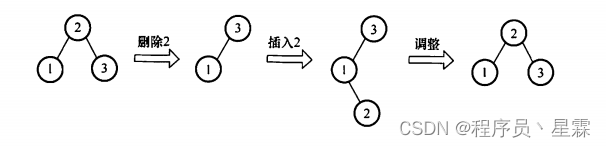
答案：A

6、下图所示是一棵（）。

• A：4阶B树
• B：4阶B+树
• C：3阶B树
• D：3阶B+树

解析

关键字数量比子树数量少1，所以不是B+树，而是B树。又因为m阶B树结点关键字数最多为m-1，有一个结点关键字个数为3，所以不可能为3阶。

答案：A

7、下列关于m阶B树的说法中，错误的是（）。

• A：根结点至多有m棵子树
• B：所有叶结点都在同一层次上
• C：非叶结点至少有m/2（m为偶数）或（m+1）/2（m为奇数）棵子树
• D：根结点中的数据是有序的

解析

除根结点外的所有非终端结点至少有$┌$m/2$┐$棵子树。对于根结点，最多有m棵子树，若其不是叶结点，则至少有2棵子树。

答案：C

8、以下关于m阶B树的说法中，正确的是（）。

Ⅰ、每个结点至少有两棵非空子树
Ⅱ、树中每个结点至多有m-1个关键字
Ⅲ、所有叶结点在同一层
Ⅳ、插入一个元素引起B树结点分裂后，树长高一层

• A：Ⅰ、Ⅱ
• B：Ⅱ、Ⅲ
• C：Ⅲ、Ⅳ
• D：Ⅰ、Ⅱ、Ⅳ

解析

每个非根的内部结点必须至少有$┌$m/2$┐$棵子树，而根结点至少要有两棵子树，所以Ⅰ不正确。Ⅱ、Ⅲ显然正确。对于Ⅳ，插入一个元素引起B树结点分裂后，只要从根结点到该元素插入位置的路径上至少有一个结点未满，B树就不会长高，如图1所示；只有当结点的分裂传到根结点，并使根结点也分裂时，才会导致树高增1，如图2所示，因此Ⅳ错误。

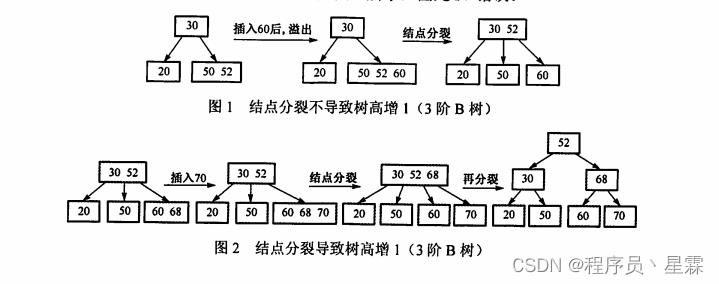
答案：B

9、具有n个关键字的m阶B树，应有（）个叶结点。

• A：n+1
• B：n-1
• C：mn
• D：nm/2

解析

B树的叶结点对应查找失败的情况，对有n个关键字的查找集合进行查找，失败可能性有n+1种。

答案：A

10、高度为5的3阶B树至少有（）个结点，至多有（）个结点。

• A：32
• B：31
• C：120
• D：121

解析

由m阶B树的性质可知，根结点至少有2棵子树；根结点外的所有非终端结点至少有$┌$m/2$┐$棵子树，结点数最少时，3阶B树形状至少类似于一棵满二叉树，即高度为5的B树至少有$2^5$-1=31个结点。

由于每个结点最多有m棵子树，所以当结点数最多时，3阶B树形状类似于满三叉树，结点数为($3^5$-1)/2=121。

答案：B。 D