很久没有做过贪心类型的题目了，因为用的很少，大多都用的dp，这道题第一眼看过去以为是dp，因为力扣里面的中等题很多都是dp，但仔细一看发现是贪心，思路其实很简单，先全部最小，中间插一个数，后面全部选最大的即可，刚开始思路错了导致错了几次后面把代码重新修改了之后就成功了，写完博客睡觉了！！！！！！

小写字符 的 数值 是它在字母表中的位置（从 1 开始），因此 a 的数值为 1 ，b 的数值为 2 ，c 的数值为 3 ，以此类推。
字符串由若干小写字符组成，字符串的数值 为各字符的数值之和。例如，字符串 "abe" 的数值等于 1 + 2 + 5 = 8 。
给你两个整数 n 和 k 。返回 长度 等于 n 且 数值 等于 k 的 字典序最小 的字符串。
注意，如果字符串 x 在字典排序中位于 y 之前，就认为 x 字典序比 y 小，有以下两种情况：
x 是 y 的一个前缀；
如果 i 是 x[i] != y[i] 的第一个位置，且 x[i] 在字母表中的位置比 y[i] 靠前。

示例 1：
输入：n = 3, k = 27
输出："aay"
解释：字符串的数值为 1 + 1 + 25 = 27，它是数值满足要求且长度等于 3 字典序最小的字符串。
示例 2：
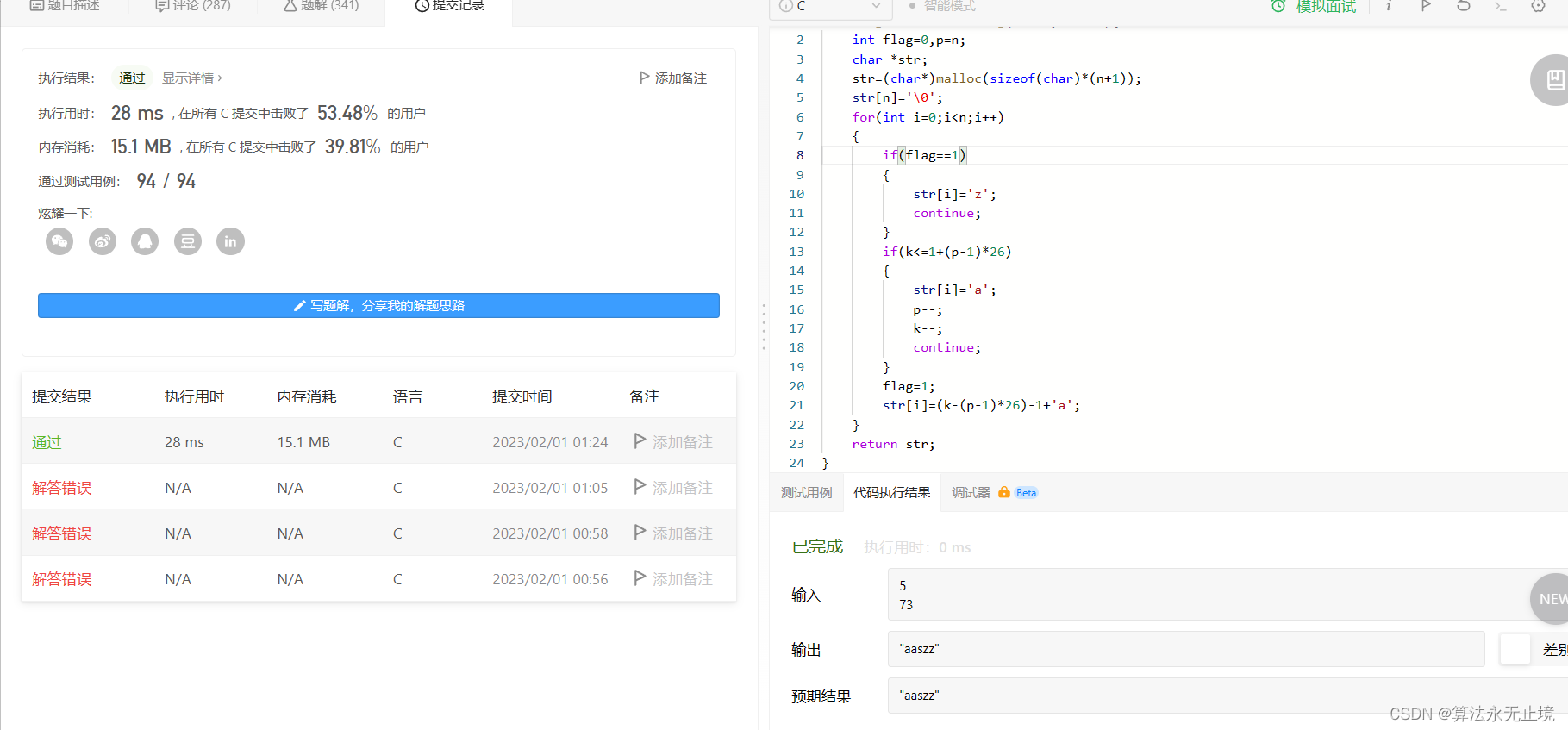
输入：n = 5, k = 73
输出："aaszz"

提示：
1 <= n <= 105
n <= k <= 26 * n

char * getSmallestString(int n, int k){
    int flag=0,p=n;
    char *str;
    str=(char*)malloc(sizeof(char)*(n+1));
    str[n]='\0';
    for(int i=0;i<n;i++)
    {
        if(flag==1)
        {
            str[i]='z';
            continue;
        }
        if(k<=1+(p-1)*26)
        {
            str[i]='a';
            p--;
            k--;
            continue;
        }
        flag=1;
        str[i]=(k-(p-1)*26)-1+'a';
    }
    return str;
}