学习目标：
理解完全背包和0-1背包遍历顺序的区别
学习内容：
15. LeetCode377. 组合总和 Ⅳ
https://leetcode.cn/problems/combination-sum-iv/
16. 爬楼梯(进阶班版)
17. LeetCode322. 零钱兑换https://leetcode.cn/problems/coin-change/
18. LeetCode279. 完全平方数https://leetcode.cn/problems/perfect-squares/
学习产出：
独立解决以上题目
15. LeetCode377. 组合总和 Ⅳ
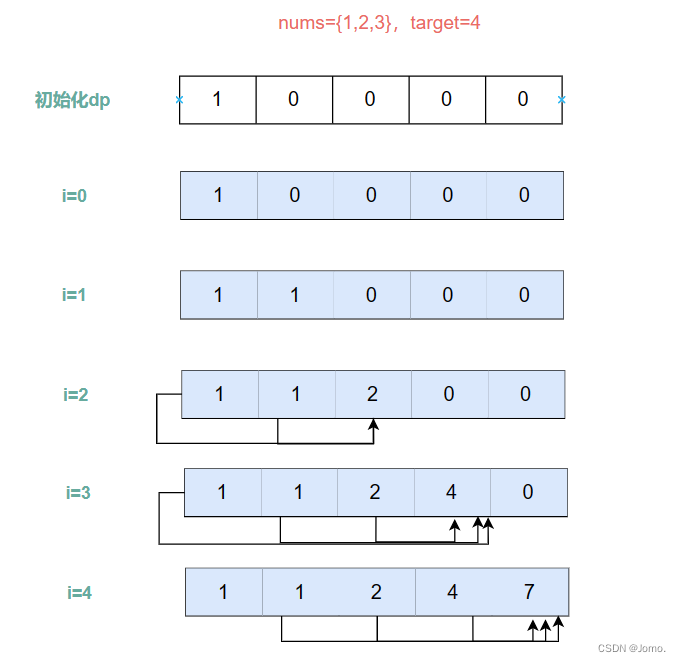
思路：本题和零钱兑换II是同一类型的题，换汤不换药
注意：顺序不同的序列视作不同的组合，因此是求排列数（元素是有序的）而不是组合数
1.dp[i]：组成i的排列个数
2.dp[i]+=dp[i-nums[j]]：只要能够获取到nums[j],dp[i-nums[j]]是dp[i]的一部分
3.初始化dp：dp[0]=1，这样递推其他数值时才有基础，其他数值初始化为0，这样才不会影响累加值
4.遍历顺序：本质上就是对于每个容量i，用nums里所有元素去组合，从最基础的开始。比如说1个1组成1，2个1组成2,1个2组成2……
4.1组合数：外层物品，内层容量
4.2排列数：外层容量，内层物品（因为物品有顺序，顺序不同组合不同，所以我们在计算每个容量的方法数时，要把每个元素每种顺序都考虑到）
4.3 eg.如果是外层遍历物品内层遍历容量，在计算dp[4]时，就会出现只有组合{1,3}而没有{3,1}，因为3只会出现在1后面
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
//dp[i]：组成i的排列个数
vector<int>dp(target+1);
//初始化dp
dp[0]=1;
//完善dp
for(int i=0;i<=target;i++){
for(int j=0;j<nums.size();j++){
//防止溢出
if(i-nums[j]>=0&&dp[i]<=INT_MAX-dp[i-nums[j]]){
//在组成i-nums[j]的基础上，用nums[j]填补，从而累加相应的方法数
//在组成dp[4]时：
//用1填补dp[3]：{1}+{1,2},{1}+{2,1},{1}+{1,1,1},{1}+{3}
//用2填补dp[2]：{2}+{1,1},{2}+{2}
//用3填补dp[1]：{3}+{1}
//不用去管dp[1],dp[2],dp[3]是怎么组成的，但是可以确定1可以出现在3后面了
//组成不同的i时，我们只遍历了一次nums里的所有元素，因此不会有重复排列出现
dp[i]+=dp[i-nums[j]];
}
}
}
return dp[target];
}
};16. 爬楼梯(进阶班版)
改为：一步1个台阶、2个台阶、3个台阶、4个台阶……直到m个台阶(每一阶可以重复使用)，求到达楼顶的总方法数。
理解：台阶就是物品，楼顶就是背包，本题被改编成了完全背包问题
1.dp[i]：爬到第i个台阶的方法数
2.dp[i]+=dp[i-j]：加入当前要走j个台阶，那么dp[i-j]就是dp[i]的一部分（从dp[i-1]累加到dp[i-j]），因为一步可以跨1~j个台阶
3.初始化dp：dp[0]是基础数值，由其推得其他dp值，所以dp[0]=1
4.遍历顺序：外背包，内物品。比如{1,2,1}和{1,1,2}实际上是不同的方法，其实就是求排列个数
int climbStairs(int m,int n){
//dp[i]：爬到第i个台阶的方法数
vector<int>dp(n+1);
//初始化dp
dp[0]=1;
//完善dp
for(int i=0;i<=n;i++){
for(int j=1;j<=i;j++){//从1个台阶开始累加
dp[i]+=dp[i-j];
}
}
return dp[n];
}17. LeetCode322. 零钱兑换
思路：
1.dp[j]：组成j的最少硬币数
2.dp[j]=min(dp[j],dp[j-coins[i]]+1)：组成j-coins[i]最少的硬币数+coins[i]这枚硬币
3.初始化dp：dp[0]=0
4.遍历顺序：外物品内背包，外背包内物品都可以。本题只是求硬币个数，所以无论硬币面额有序还是无序都不影响。
外物品内背包：
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
//dp[j]：组成j的最少硬币数
vector<int>dp(amount+1,INT_MAX-1);//不影响最小值判断
//初始化dp
dp[0]=0;
//完善dp
for(int i=0;i<coins.size();i++){
for(int j=coins[i];j<=amount;j++){
dp[j]=min(dp[j],dp[j-coins[i]]+1);
}
}
return dp[amount]==INT_MAX-1?-1:dp[amount];
}
};
外背包内物品：
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int>dp(amount+1,INT_MAX-1);
dp[0]=0;
for(int i=0;i<=amount;i++){
for(int j=0;j<coins.size();j++){
if(i-coins[j]>=0)dp[i]=min(dp[i],dp[i-coins[j]]+1);
}
}
return dp[amount]==INT_MAX-1?-1:dp[amount];
}
};18. LeetCode279. 完全平方数
思路：
1.dp[i]：和为i的完全平方数的最少数量
2.dp[i]=min(dp[i],dp[i-j*j]+1)
3.初始化dp：vector<int>dp(n+1,INT_MAX-1)，dp[0]=0
4.遍历顺序：由于是求个数，所以无论哪种顺序都可以
class Solution {
public:
int numSquares(int n) {
//dp[i]：和为i的完全平方数的最少数量
vector<int>dp(n+1,INT_MAX-1);
//初始化dp
dp[0]=0;
//完善dp
for(int i=1;i<=n;i++){
for(int j=1;j*j<=i;j++){
dp[i]=min(dp[i],dp[i-j*j]+1);
}
}
return dp[n]==INT_MAX?-1:dp[n];
}
};
j^2不是j的平方，而是j异或2总结：题目要我们返回什么结果，动态规划表就表达什么意思。注意遍历顺序：如果是求组合数，就外物品内背包；如果是求组合数，就外背包内物品。
