题目1：N皇后
按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

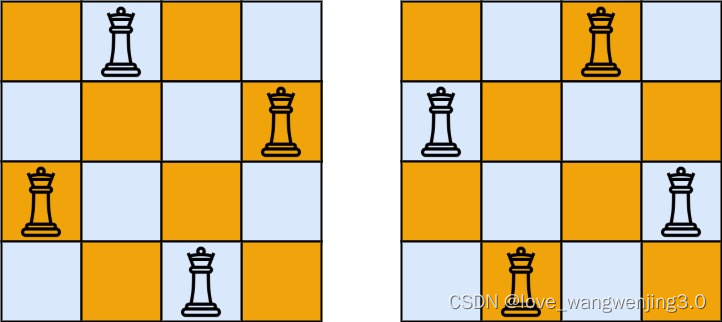
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。
分析思路：
首先明确此问题限制条件：每一横行，竖行，斜行不能出现超过一个皇后
可以考虑运用unordered_set来记录unordered_set的优点(去重容器)
1.直接存取数据的值，对比unordered_map<int,int>
2.容器内部各元素不相等
3.不会将元素按照key值排序，对比ordered_set
需要一个queen变量来存放每一行皇后放的具体列，之后打印面板board（用"Q",“.”）来打印二维数组，至于怎么得到正确的皇后的位置，应该采用逐个遍历，但是普通循环解决不了这个问题，本质上是在逐个尝试，当发现不合适时及时退出，所以采用回溯方法

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        unordered_set<int>columns;//容易内部各元素不能相同
        unordered_set<int>dial1;
        unordered_set<int>dial2;
       auto solution=vector<vector<string>>();
       auto queens=vector<int>(n,-1);
       backtrack(solution,queens,n,0,columns,dial1,dial2);
       return solution;
    }
    void backtrack(vector<vector<string>>& solution,vector<int>&queens,int n,int row,unordered_set<int>&columns,unordered_set<int>&dial1,unordered_set<int>&dial2)
    {
        if(row==n){
            vector<string> board= generateboard(queens,n);
            solution.push_back(board);
            }
        else
        {
            for(int i=0;i<n;i++)
            {
                if(columns.find(i)!=columns.end())
                {
                    continue;
                }
                int dial_1= row-i;//同一条斜线上的每个位置满足行下标与列下标之差相等(0,0) 和(3,3) ,i代表列
                if(dial1.find(dial_1)!=dial1.end())//要保证dial1中没有出现过当前值
                {
                    continue;
                }
                int dial_2=row+i;
                if(dial2.find(dial_2)!=dial2.end())
                {
                    continue;
                }
                queens[row]=i;//在所有不满足条件进行之后  才开始插入
                columns.insert(i);
                dial1.insert(dial_1);
                dial2.insert(dial_2);
                backtrack(solution, queens, n, row + 1, columns, dial1, dial2);//回溯
                queens[row]=-1; //回溯之后要重置
                columns.erase(i);//之前插入的不符合条件的需要删除
                dial1.erase(dial_1);
                dial2.erase(dial_2);
            }
        }
    }

     vector<string> generateboard(vector<int> &queens, int n) {
        auto board = vector<string>();
        for (int i = 0; i < n; i++) {
            string row = string(n, '.');//初始化全部置为....
            row[queens[i]] = 'Q';//queens[i] //代表第i行的皇后应该放的列的位置
            board.push_back(row);
        }
        return board;
    }
};

题目二：N皇后二
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

class Solution {
public:
    int totalNQueens(int n) {
        unordered_set<int>colunms;
        unordered_set<int>dia1s;
        unordered_set<int>dia2s;
        vector<int>queens(n,-1);
        //int solve_cnt=0;
        //backtrack(colunms,dia1s,dia2s,0,queens,solve_cnt,n);
        return backtrack(colunms,dia1s,dia2s,0,queens,n);
    
    }
    int backtrack(unordered_set<int>&colunms,unordered_set<int>&dia1s,unordered_set<int>&dia2s,int row,vector<int>&queens,int n)
    {
        if(row==n)
        {
            return 1;
        }
        else
        {
            int count=0;
            for(int i=0;i<n;i++)
            {
                if(colunms.find(i)!=colunms.end())
                {
                    continue;
                }
                //colunms.insert(i);//i代表列
                int dia1=row+i;
                if(dia1s.find(dia1)!=dia1s.end())
                {
                    continue;
                }
                //dia1s.insert(dia1);
                int dia2=row-i;
                if(dia2s.find(dia2)!=dia2s.end())
                {
                    continue;
                }
                colunms.insert(i);//i代表列 //在所有不满足条件进行之后  才开始插入
                dia1s.insert(dia1);
                dia2s.insert(dia2);
                queens[row]=i;
                count+=backtrack(colunms,dia1s,dia2s,row+1,queens,n);
                colunms.erase(i);
                dia1s.erase(dia1);
                dia2s.erase(dia2);
                queens[row]=-1;                          
                }
            return count;
        }
    }
};