很多好主意一旦踏上语义鸿沟，就再也听不到。

---

卷积，在图像、视觉领域乃老生常谈的内容，但是对于具体工作细节仍然值得我去学习。

卷积原理

卷积，就是利用一个小的矩阵(或者更高维向量)作用于图像矩阵(或者特征矩阵)，然后输出特定且有意义的值。

具体来讲，该过程被称为特征映射，每一个特征映射都是一类图像特征。
如对于一张带有猫的图像，使用三个卷积核作用于这个图像，每个卷积核卷积后的结果为一种特征映射结果。如三个卷积核分别倾向于猫耳朵、猫脚、猫尾巴特征。
那么通过增加使用的卷积核数量，可以更好地掌握图像地特征。

在实际应用中，如需要对MNIST数据集中地数字进行识别，由于MNIST数据集中的图片均为灰度图，那么就存在一个特征映射（至少）；相应的，如果是RGB图片，那么存在三个特征映射（至少），每个通道一个映射。

卷积核的大小设定与特征图有一定的关系，如果特征图为蓝色部分，绿色为卷积核，可知卷积核的层数与特征图的层数保持一致，如将特征图的$L_1$与卷积核的$W_1$进行点乘，$L_2$与$W_2$进行点乘…$L_n$与$W_n$进行点乘，最后得到一个一维向量，该向量的维度为特征图(或卷积核)层数，并将该一维向量进行累计求和，最后得到一个数值(特征值)。

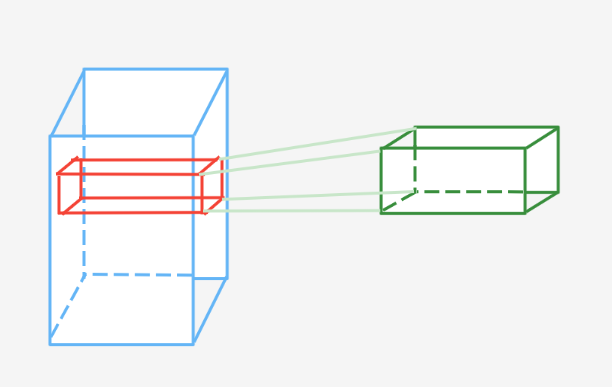
更为具体形象的描述如下图（引用自邱锡鹏的《神经网络与深度学习》）

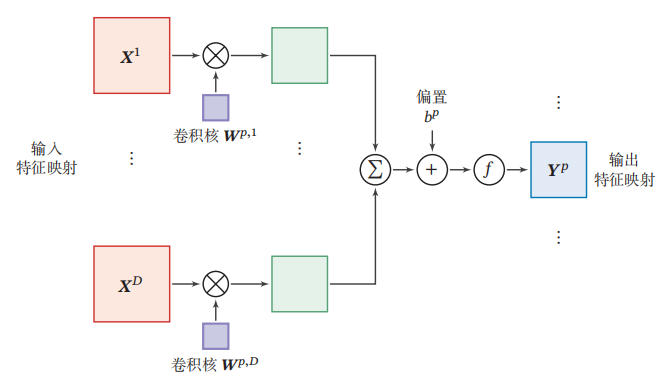
上图中$X^1...X^D$均为一张特征图的不同层，$W^{p,1}...W^{p,D}$为一个卷积核的不同层，分别点乘求和，然后加入偏置（每一个求和结果加入偏置值），并经过激活函数得到特征映射。
PS:偏置的目的在于使特征提取更加灵活，对信息进行权重衡量，调整比例。

---

卷积运用

卷积层替换全连接层。

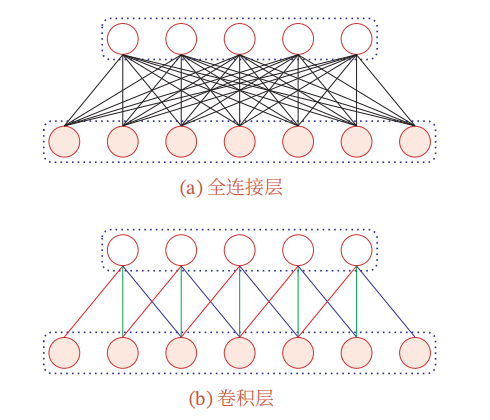
卷积层作用于局部区域特征融合，全连接层作用于全局特征信息融合，两者区别在于作用区域范围不同，存在可置换的可能性。

但卷积层替换全连接层的原因何在？

全连接层与前一层的参数数量是固定的，导致对于卷积输入的图像大小固定，这一限制导致很多任务存在时间耗时、训练繁杂等问题。而是用卷积操作，卷积核的数量与前一层的特征图的大小没有影响关系，即可解决图像大小限制问题。
如输入512x512x3的图片，全连接层前一层的特征图为16x16x8，全连接层有128个神经元，那么我们可以使用128个16x16x8的卷积核进行卷积操作，输出11128的特征图。

卷积结果分析

通用的卷积神经网络结果尺寸计算公式为
$$\begin{array}{r}N=\frac{(输入尺寸-卷积核尺寸+2\ast 填充尺寸)}{步长stride}+1\end{array}$$

库函数
nn.Conv2d(in_channels,out_channels,kernel_size,stride,padding)

如输入图像大小为227x227X3，卷积核的大小为5x5x3，padding为3，stride=2,那么卷积结果尺寸为$\frac{227-5+2\ast 3}{2}+1=115$

---

卷积求导运算

卷积中主要关注卷积核参数与偏置系数，按照误差反向传播进行参数更新优化。

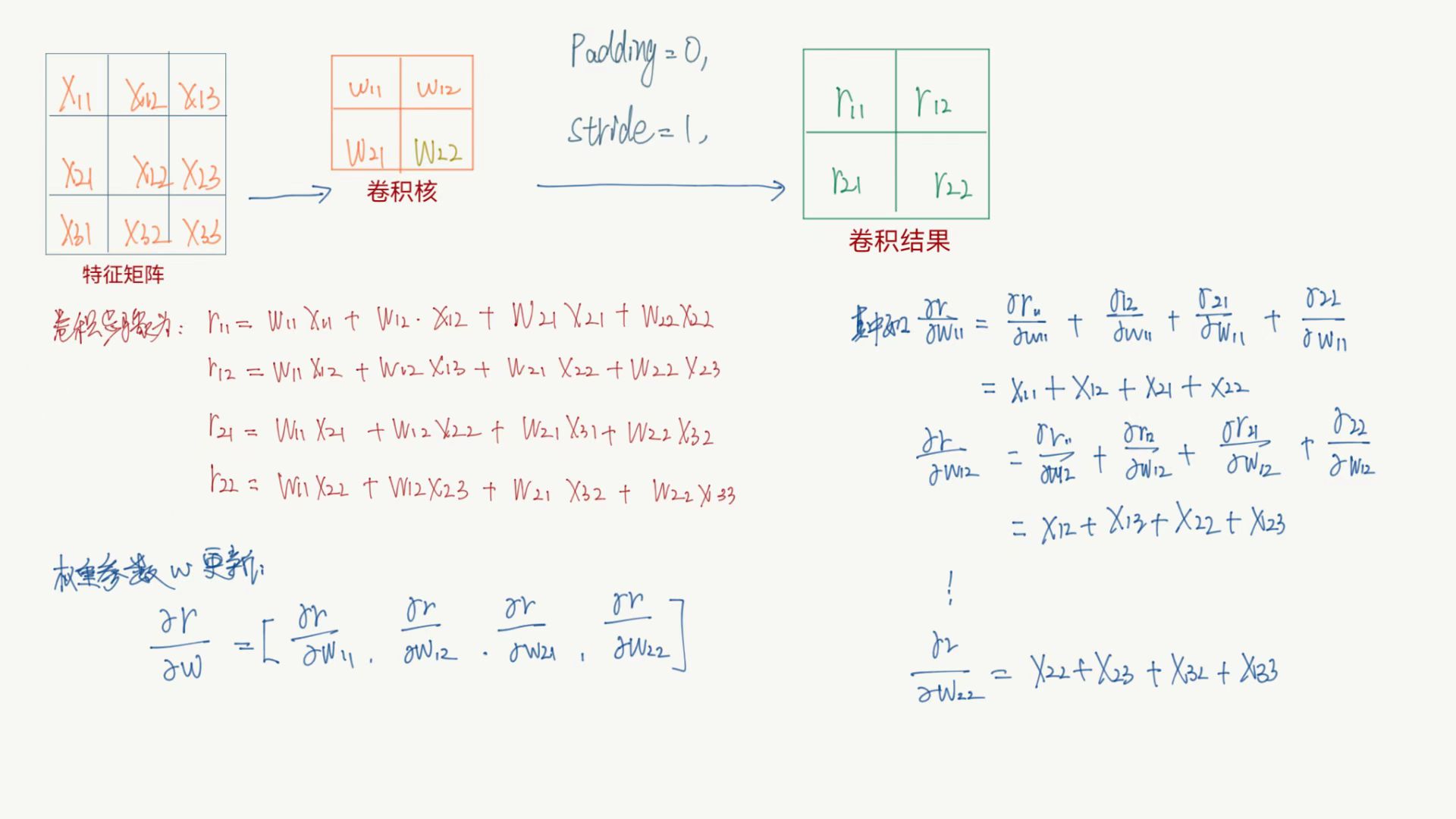
当然，一般还有激活层，只需将结果先对激活函数求导，激活函数对各个参数求导即可。