目录
一.邻接矩阵
1.1概念介绍
1.2代码示例
1.3代码测试
二.邻接表
2.1概念介绍
2.2代码示例:
2.3代码测试
三.遍历
3.1广度优先遍历(BFS)
3.1.1邻接表(BFS)
3.1.2邻接矩阵(BFS)
3.2深度优先遍历(DFS)
3.2.1邻接表(DFS)
3.2.2邻接矩阵(DFS)
一.邻接矩阵
1.1概念介绍
邻接矩阵(二维数组)即是:先用一 个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。矩阵可以存储0或者1来表示两个顶点之间是否连通,也可以存储权值。. 用邻接矩阵存储图是能够快速知道两个顶点是否连通,缺陷是如果顶点比较多,边比较少时,矩阵中存储了大量值为0的矩阵,比较浪费空间,并且要求两个节点之间的路径不是很好求。
例如:

上面的邻接矩阵中,如果两个顶点之间不连通的话,用无穷大来表示。上面的是有向图,无向图的矩阵是对称的。
1.2代码示例
我们需要存储各个顶点以及顶点之间边的信息。存储边的信息可以用一个二维数组来表示,这里会用到下标,所以可以用一个map来存储顶点与对应下标的映射关系。
template<class V,class W, W W_MAX=INT_MAX,bool Direc=false>// v表示边的类型,W表示权值类型,W_MAX默认为INT_MAX
class Grap
{
public:
Grap(const V* a,int n)
{
_vertexs.resize(n);
for (int i = 0; i < n; i++)
{
_vertexs[i] = a[i]; //顶底集合初始化
_indexMap[a[i]] = i; //映射初始化
}
_matrix.resize(n);
for (size_t i = 0; i < _matrix.size(); ++i) //矩阵初始化
{
_matrix[i].resize(n, 0);
}
}
int get_index(const V a)
{
auto it = _indexMap.find(a);
if (it != _indexMap.end())
{
return it->second;
}
else
{
exit(-1);
}
}
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
_matrix[srci][dsti] = w;
if (Direc == false)// 无向图
{
_matrix[dsti][srci] = w;
}
}
void AddEdge(const V& src, const V& dst, const W& w)//添加两个顶点的边,附上权值
{
int srci = get_index(src);
int dsti = get_index(dst);
_AddEdge(srci, dsti, w);
}
void Print()
{
int n = _vertexs.size();
cout << " ";
for (int i = 0; i < n; i++)
{
printf("%-3c", _vertexs[i]);
}
cout << endl;
for (int i = 0; i < n; i++)
{
cout << _vertexs[i] << " ";
for (int j = 0; j < n; j++)
{
//cout << _matrix[i][j] << " ";
printf("%3d", _matrix[i][j]);
}
cout << endl;
}
}
private:
vector<V> _vertexs; // 顶点集合
map<V, int> _indexMap; // 顶点映射下标
vector<vector<W>> _matrix; // 邻接矩阵
};1.3代码测试
int main()
{
char a[] = "ABCDE";
Grap<char, int> G(a,5);
G.AddEdge('A', 'B', 7);
G.AddEdge('A', 'D', 3);
G.AddEdge('C', 'D', 4);
G.AddEdge('C', 'E', 6);
G.Print();
return 0;
}结果:

二.邻接表
2.1概念介绍
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
无向图邻接表存储,例如:
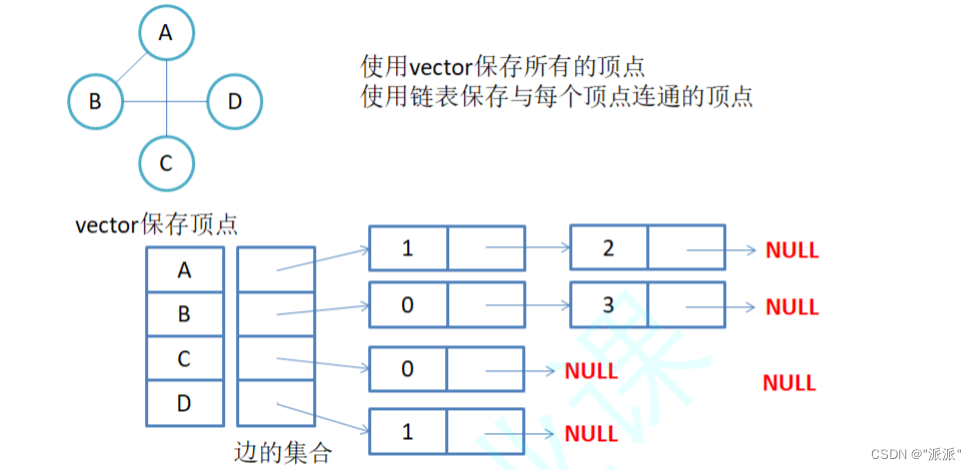
有向图邻接表存储,例如:
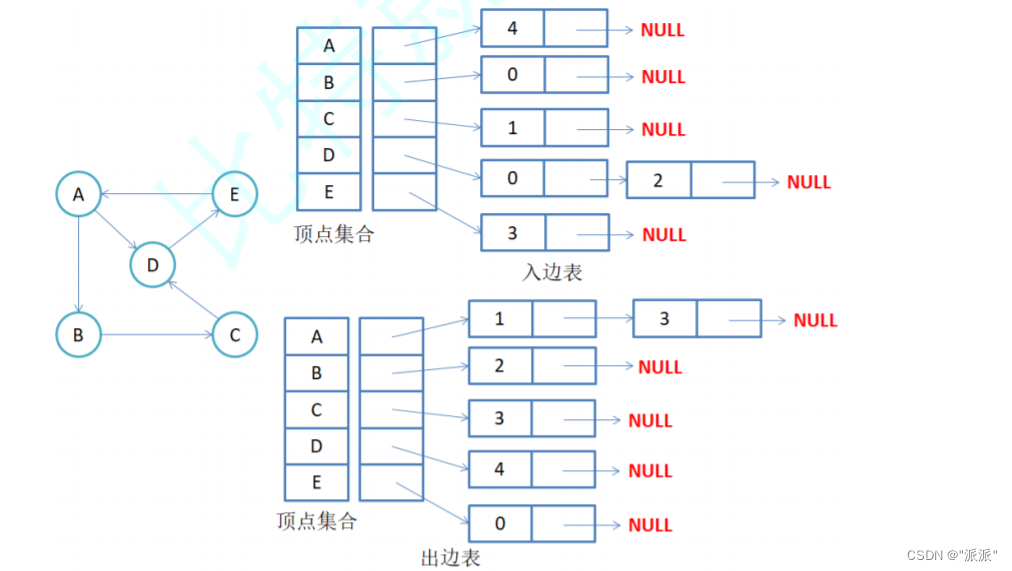
2.2代码示例:
template<class W>
struct Edge
{
int _dsti; // 目标点的下标
W _w; // 权值
Edge<W>* _next;
Edge(int dsti, const W& w)
:_dsti(dsti)
, _w(w)
, _next(nullptr)
{}
};
template<class V, class W, W W_MAX = INT_MAX, bool Direc = false>// v表示边的类型,W表示权值类型,W_MAX默认为INT_MAX
class LinkTable
{
typedef Edge<W> Edge;
public:
LinkTable(const V* a, int n)
{
_vertexs.resize(n);
for (int i = 0; i < n; i++)
{
_vertexs[i] = a[i]; //顶底集合初始化
_indexMap[a[i]] = i; //映射初始化
}
_linkTable.resize(n,nullptr);
}
int get_index(const V& a)
{
auto it = _indexMap.find(a);
if (it != _indexMap.end())
{
return it->second;
}
else
{
exit(-1);
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
int srcindex = get_index(src);
int dstindex = get_index(dst);
Edge* E = new Edge(dstindex, w);
E->_next = _linkTable[srcindex];
_linkTable[srcindex] = E;
if (Direc == false)
{
Edge* E = new Edge(srcindex, w);
E->_next = _linkTable[dstindex];
_linkTable[dstindex] = E;
}
}
void Print()
{
for (int i = 0; i < _vertexs.size(); i++)
{
cout << _vertexs[i]<<":>>";
Edge* E = _linkTable[i];
while (E)
{
cout << _vertexs[E->_dsti] << ":" << E->_w << "->";
//printf("%c -> %d", _vertexs[E->_dsti], E->_w);
E = E->_next;
}
cout <<"nullptr"<< endl;
}
}
private:
vector<V> _vertexs; // 顶点集合
map<V, int> _indexMap; // 顶点映射下标
vector<Edge*> _linkTable; // 邻接矩阵
};2.3代码测试
int main()
{
char a[] = "ABCDE";
LinkTable<char, int> G(a,5);
G.AddEdge('A', 'B', 7);
G.AddEdge('A', 'D', 3);
G.AddEdge('C', 'D', 4);
G.AddEdge('C', 'E', 6);
G.Print();
return 0;
}结果:

三.遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶 点只能被遍历一次。
3.1广度优先遍历(BFS)
什么是广度优先遍历呢?例如:
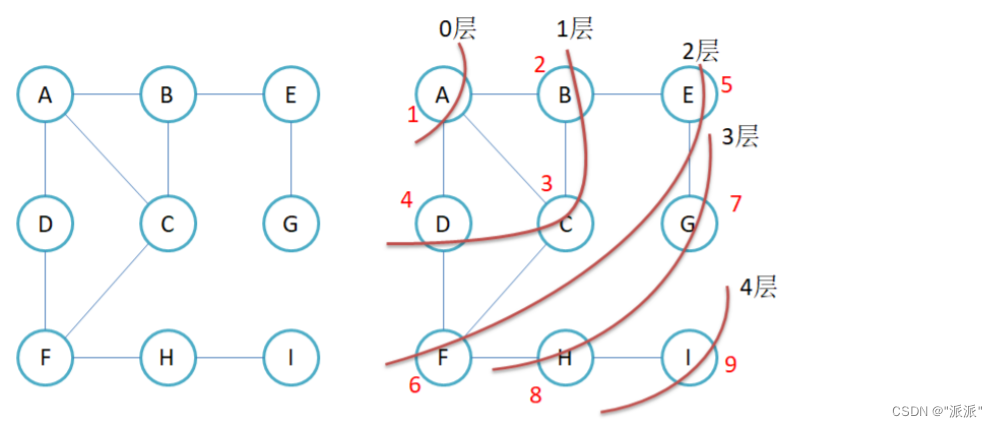
假设上面的图已经存储好了,从A点开始遍历图,要将所有的顶点都遍历一次。上面的0层,1层,2层....就是遍历顺序,每次把与当前层顶点相连的顶点都要遍历一次,再去遍历下一层。
由于只是要遍历与上一层顶点相连的顶点,若图比较稀疏,用邻接矩阵去遍历点时,遍历每个点都要O(n)的时间复杂度,所以用邻接表比较适合存储。
3.1.1邻接表(BFS)
先看下邻接表的存储结果

假如先从A点开始遍历,第0层可以直接输出A这个顶点,由表可知,与A顶点相连的有D,B两点。可将其放入队列中,出队列时将当前层的顶点出完(同时把与顶点相连的点放入队列),同时还要判断当前顶点是否被访问过。
要注意上面邻接表中,例如_linkTable[0]存储的是D顶点的信息,这样便于操作。
代码示例:
void BFS(const V& a)
{
int src = get_index(a);
queue<Edge*> _q;
vector<bool> v(_vertexs.size(), true);
v[src] = false; //当前起始顶点访问过。设置为false
cout <<"0"<<" : "<< _vertexs[src] << endl;
Edge* cur = _linkTable[src];
while (cur) //把与起始点相连的点入队列
{
_q.push(cur);
v[cur->_dsti] = false; //入队列就认为访问过,后面入队列判断是否为false
cur = cur->_next;
}
int levesize = _q.size();
int k = 1;
while (!(_q.empty()))
{
cout << k << " : ";
while (levesize--)
{
Edge* e = _q.front();
cout << _vertexs[e->_dsti] <<" ";
Edge* cur = _linkTable[e->_dsti];
while (cur)
{
if (v[cur->_dsti]) //判断该顶点是否入过队列了
{
_q.push(cur);
v[cur->_dsti] = false;
}
cur = cur->_next;
}
_q.pop();
}
levesize = _q.size();
k++;
cout << endl;
}
}
结果测试:
int main()
{
char a[] = "ABCDEFGHI";
Grap<char, int> G(a, sizeof(a)/sizeof(a[0])-1);
G.AddEdge('A', 'B', 7);
G.AddEdge('A', 'D', 3);
G.AddEdge('A', 'C', 4);
G.AddEdge('B', 'E', 6);
G.AddEdge('B', 'C', 9);
G.AddEdge('C', 'F', 1);
G.AddEdge('D', 'F', 12);
G.AddEdge('E', 'G', 13);
G.AddEdge('F', 'H', 19);
G.AddEdge('H', 'I', 29);
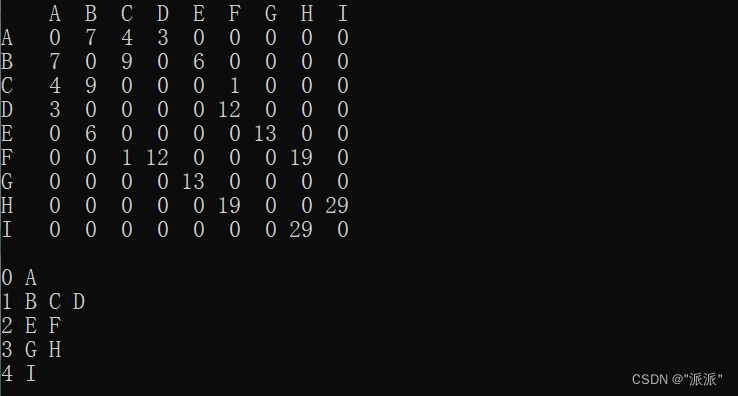
G.Print();
cout << endl;
G.BFS('A');
return 0;
}上面的顶点创建的图为:
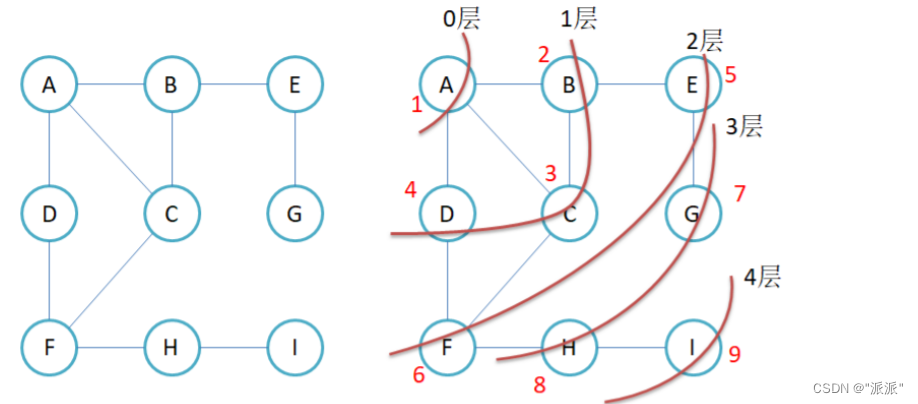
结果:

3.1.2邻接矩阵(BFS)
思路是一样的,直接上代码吧
void BFS(const V& a)
{
int src = get_index(a);
queue<int> _q;
vector<int> v(_vertexs.size(), true);
_q.push(src);
v[src] = false;
int levesize = 1;
int k = 0;
while (!_q.empty())
{
cout << k << " ";
while (levesize--)
{
int cur = _q.front();
_q.pop();
cout << _vertexs[cur]<<" ";
for (int i = 0; i < _vertexs.size(); i++)
{
if (_matrix[cur][i] != 0 && v[i])
{
_q.push(i);
v[i] = false;
}
}
}
levesize = _q.size();
k++;
cout << endl;
}
}结果:
3.2深度优先遍历(DFS)
概念:一条道走到黑,例如:
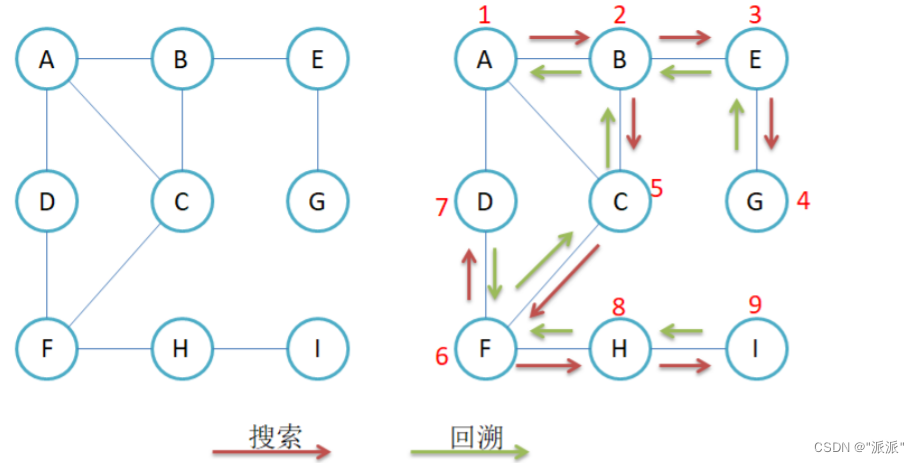
3.2.1邻接表(DFS)
void _DFS(const V& a,vector<bool>& v)
{
int src = get_index(a);
Edge* cur = _linkTable[src];
while (cur)
{
if (cur)
{
if (v[cur->_dsti]) //判断当前点是否被访问
{
cout << _vertexs[cur->_dsti] << " ";
v[cur->_dsti] = false;
V p = _vertexs[cur->_dsti]; //p为当前点
_DFS(p, v); //根据p可找到与p相连的点,递归处理
}
cur = cur->_next; //找p的下一个点
}
}
}
void DFS(const V& a)
{
int src = get_index(a);
vector<bool> v(_vertexs.size(), true); //记录顶点是否被访问过
v[src] = false; // 起始点设置为false
cout << _vertexs[src] << " ";
_DFS(a, v);
}3.2.2邻接矩阵(DFS)
思路类似的
void DFS(const V& a)
{
vector<bool> v(_vertexs.size(), true);
int src = get_index(a);
v[src] = false;
_DFS(a, v);
}
void _DFS(const V& a, vector<bool>& v)
{
int cur = get_index(a);
cout << a << " ";
for (int i = 0; i < v.size(); i++)
{
if (v[i] && _matrix[cur][i] != 0)
{
v[i] = false;
_DFS(_vertexs[i], v);
}
}
}