函数极限与连续
文章目录
- 函数极限与连续
- 1.函数概念与特性
- 1.1 函数定义
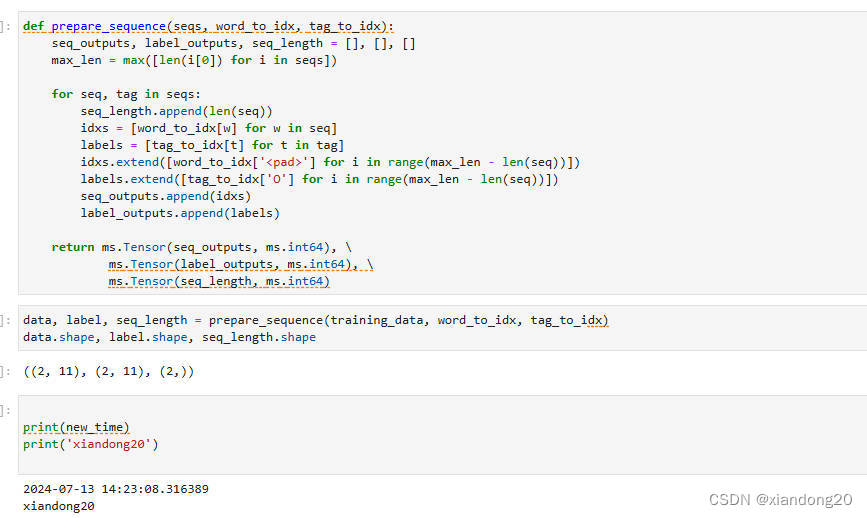
- 1.2 几种重要的基本函数类型
- 1.2.1 反函数
- 1.2.2 复合函数
- 1.2.3 隐函数
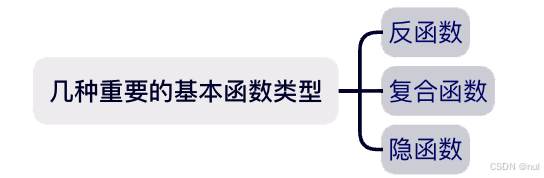
- 1.3 函数的基本特性
- 1.3.1 有界性
- 1.3.2 单调性
- 1.3.3 奇偶性
- 1.3.4 周期性
- 2. 函数的极限
- 2.1函数的极限的定义
- 2.2 函数的极限的性质
- 2.3 无穷小
- 2.3.1 无穷小基础知识
- 2.3.2 无穷小进阶知识
- 3. 函数极限的计算
- 3.1 计算工具
- 3.2 七种未定式的计算
- 4.函数的连续和间断
- 4.1 基础知识
- 4.2 进阶知识
- 4.2.1 连续函数性质的推广
1.函数概念与特性
1.1 函数定义
x自变量,y因变量,f对应法则,记作y=f(x)
关于定义域的概念一定要弄懂,
f(x+1)的定义域是[0,a],是说里面的x变化是0到a,而不是 0≤x+1≤a
1.2 几种重要的基本函数类型
1.2.1 反函数
反函数:x=φ(y)
如何判断某个函数是否有反函数?
答:竖直铅锤画线,看交点。两个交点就无反函数。
注意的点:
1.严格单调函数必有反函数
2.关于反函数的图像问题:
x=f-1(y)与y=f(x)的图像画在同一坐标系下是完全重合的,只有在交换他们的字母之后,即把x=f-1(y)写成y=f-1(x)后,它们才关于y=x重合。
1.2.2 复合函数
y=f[g(x)]
注意的点:
1.复合函数的定义域是两个函数的交集
1.2.3 隐函数
顾名思义,不好写成y=f(x)的形式,只能混搭的函数。
1.3 函数的基本特性
1.3.1 有界性
很好理解,x属于区间I,|f(x)|≤M,则称f(x)在区间I上有界,反之无界。
有界的判定:
看到闭区间,闭区间连续,必有界
看到开区间,开区间求两边极限,极限存在就有界。
看到导数,导数在区间上有界,原函数有界。
有界意味着函数既有上界又有下界
1.3.2 单调性
区间I上两点x1,x2
当x1<x2,恒有f(x1)<f(x2),则叫单调递增。
当x1<x2,恒有f(x1)>f(x2),则叫单调递增。
f’(x)>0,f(x) 单调增加
f’(x)≤0,f(x) 单调不减
注意这里是导函数大于0,然后…,可不是某点
易错点:
一点导数>0,推不出临域单调增加
但是假如该点存在2阶导数,说明一阶导数该点临域连续,若该点导数大于0,就可以说明临域是单调增加的了
1.3.3 奇偶性
定义:
偶函数:f(-x)=f(x)
奇函数:f(-x)=-f(x)
一眼能看出来
常见奇函数:sinx,tanx,arcsinx,arctanx
常见偶函数:cosx,x2,|x|
图像性质:
奇函数关于原点对称,且若f(x)在x=0处有定义,则f(0)=0
偶函数关于y轴对称。
奇偶性的判定:
- 函数求导,奇偶性改变
- 复合函数,内偶则偶,内奇同外
- 若
f
(
x
)
f\left(x\right)
f(x)是奇函数,则
∫
0
x
f
(
t
)
d
t
\int_{0}^{x}f\left(t\right)dt
∫0xf(t)dt,是偶函数
若 f ( x ) f\left(x\right) f(x)是偶函数,则 ∫ 0 x f ( t ) d t , \int_{0}^{x}f\left(t\right)dt, ∫0xf(t)dt,是奇函数。
1.3.4 周期性
定义:f(x+T)=f(x)
周期函数的原函数是周期函数的充要条件是其在一个周期上的积分为0
2. 函数的极限
邻域:x0是数轴上的一个点,存在一个正数ξ,称(x0-ξ,x0+ξ)为点x0的邻域
2.1函数的极限的定义
函数极限的定义:
函数某点在一个去心邻域内有定义,存在一个大于0的值(无论它多小),|f(x)-A|小于这个值
核心:函数极限在某点存在的前提是函数在该点去心临域有定义,就是该点去心临域内函数存在。
2.2 函数的极限的性质

唯一性: 极限存在,极限唯一
局部有界性(极限控制函数):
x趋向于x0极限存在=A,则存在一个正常数M和ξ,使得当0<|x-x0 |<ξ时,有|f(x)|<=M
简言之,趋近于某点的极限存在,则它周围的小范围内,函数有界
局部保号性:
函数极限大于0,在它的邻域内,无穷多个小点都大于0,所以f(x)大于0,反之,小于0,思考一下,为什么我们要求这个极限大于0小于0,而不是=0呢,如果极限=0,他周围的无穷小点,他左边的点一定小于0,右边大于0
戴帽法和脱帽法:
理解了上面的保号性,再理解脱帽和戴帽就简单了,lim f>0,去掉极限符号 f>0,反之成立(如果=0,f(x)就可正可负了。f>=0,lim f>=0,(没有任何问题)
摘帽法,戴帽法,注意我们应该说明是在去心临域内,简言之,脱帽不能随意加等号.
2.3 无穷小
本小节,为考试的重点章节
2.3.1 无穷小基础知识
无穷小的定义:x趋近于某一个值,也可能是无穷,我们把趋近的这个过程叫做无穷小。
无穷小的性质:
- 有限个无穷小的和是无穷小
- 有界函数与无穷小的乘积是无穷小
- 有限个无穷小的乘积是无穷小
无穷小的比阶:
首先明白,0是最高阶的无穷小.
两个函数之比的极限:
=0,分子是分母的高阶无穷小.
=∞,分子是分母的低阶无穷小.
=1,分子是分母的等阶无穷小.
=a 分子是分母的同阶无穷小.
常用的等价无穷小:
明白无穷小的等价代换是一个过程,我们使用的过程中要将他推广,sinx中的x无论是什么,只要他这个整体是趋于0的过程,那他等价于x
x→0时,常用的等价无穷小:
sin
x
∼
x
,
tan
x
∼
x
,
arcsin
x
∼
x
,
ln
(
x
+
1
)
∼
x
,
e
x
−
1
∼
x
ln
(
x
+
1
+
x
2
)
=
x
,
1
−
cos
x
=
1
2
x
2
,
1
−
cos
n
x
=
n
2
x
2
a
x
−
1
=
x
ln
a
,
(
1
+
x
)
a
−
1
=
a
x
\sin x \sim x, \quad \tan x \sim x, \quad \arcsin x \sim x, \quad \ln(x + 1) \sim x, \quad e^{x} - 1 \sim x \\ \ln\left(x + \sqrt{1 + x^{2}}\right) = x, \quad 1 - \cos x = \frac{1}{2}x^{2}, \quad 1 - \cos^n x = \frac{n}{2}x^{2} \quad \\\ a^{x} - 1 = x\ln a, \quad (1 + x)^{a} - 1 = ax
sinx∼x,tanx∼x,arcsinx∼x,ln(x+1)∼x,ex−1∼xln(x+1+x2)=x,1−cosx=21x2,1−cosnx=2nx2 ax−1=xlna,(1+x)a−1=ax
2.3.2 无穷小进阶知识
在比较阶数的过程中,有下面几种方法很好用
- 求导定阶
如果正常比较不好比较,那么就求导数比较,导数和原函数阶数差1
2. lim x → 0 f ( x ) g ( x ) = 1 , 则 ∫ 0 φ ( x ) f ( t ) d t = ∫ 0 φ ( x ) g ( t ) d t , 其中 lim x → 0 φ ( x ) = 0 2. \lim \limits_{x\rightarrow 0}\frac{f\left(x\right)}{g\left(x\right)} = 1,则\int \limits_{0}^{\varphi \left(x\right)}f\left(t\right)dt = \int \limits_{0}^{\varphi \left(x\right)}g\left(t\right)dt,其中\lim \limits_{x\rightarrow 0}\varphi \left(x\right) = 0 2.x→0limg(x)f(x)=1,则0∫φ(x)f(t)dt=0∫φ(x)g(t)dt,其中x→0limφ(x)=0
x→0,两函数极限比值=1,则他们的定积分同阶,积分上限趋近于0,下限为0
3.变上限积分定阶结论
前提
:
f
(
x
)
在
x
=
0
的某邻域内连续
,
且
f
(
x
)
是
x
的
m
阶无穷小
,
φ
(
x
)
是
x
的
n
阶无穷小
则
x
→
0
时
,
F
(
x
)
=
∫
0
φ
(
x
)
f
(
t
)
d
t
是
x
的
n
∗
(
m
+
1
)
阶无穷小
\:前提:f(x)在x = 0的某邻域内连续,且f(x)是x的m阶无穷小,\varphi \left(x\right)是x的n阶无穷小\\则x\rightarrow 0时,F\left(x\right) = \int \limits_{0}^{\varphi \left(x\right)}f\left(t\right)dt是x的n*\left(m + 1\right)阶无穷小
前提:f(x)在x=0的某邻域内连续,且f(x)是x的m阶无穷小,φ(x)是x的n阶无穷小则x→0时,F(x)=0∫φ(x)f(t)dt是x的n∗(m+1)阶无穷小
3. 函数极限的计算
高等数学三大计算之一,非常重点
3.1 计算工具
一.极限的四则运算方法
在满足极限分别存在的前提条件下,极限的加减乘除四则运算都存在。
二.洛必达法则
右存在→左存在,上下求导之后,导数比极限存在→原式存在
洛必达失效的几种情况:
- 不是0/0或∞/∞
- 求导之后的函数极限不能化简
- 不满足分子分母可导,保证去心邻域内可导.
- 求导之后的极限存在或者是无穷大,所于求导之后是振荡不存在,洛必达法则失效.
三.泰勒公式
前提:f(x)在x=0除可导.
f(x)=f(0)+f’(x)x+(f’'(x)/2!)x2…
重要函数的泰勒公式:
sin
x
=
x
−
x
3
3
!
+
o
(
x
3
)
,
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
+
o
(
x
4
)
arcsin
x
=
x
+
x
3
3
!
+
o
(
x
3
)
,
tan
x
=
x
+
x
3
3
,
arctan
x
=
x
−
x
3
3
+
o
(
x
3
)
ln
(
1
+
x
)
=
x
−
x
2
2
+
x
3
3
+
o
(
x
3
)
e
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
o
(
x
3
)
(
1
+
x
)
a
=
1
+
a
x
+
a
(
a
−
1
)
2
!
x
2
+
o
(
x
2
)
\sin x = x - \frac{x^{3}}{3!} + o\left(x^{3}\right), \quad \cos x = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + o\left(x^{4}\right) \\ \arcsin x = x + \frac{x^{3}}{3!} + o\left(x^{3}\right), \quad \tan x = x + \frac{x^{3}}{3}, \quad \arctan x = x - \frac{x^{3}}{3} + o\left(x^{3}\right) \\ \ln \left(1 + x\right) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + o\left(x^{3}\right) \\ e^{x} = 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + o\left(x^{3}\right) \\ \left(1 + x\right)^{a} = 1 + ax + \frac{a\left(a - 1\right)}{2!}x^{2} + o\left(x^{2}\right)
sinx=x−3!x3+o(x3),cosx=1−2!x2+4!x4+o(x4)arcsinx=x+3!x3+o(x3),tanx=x+3x3,arctanx=x−3x3+o(x3)ln(1+x)=x−2x2+3x3+o(x3)ex=1+x+2!x2+3!x3+o(x3)(1+x)a=1+ax+2!a(a−1)x2+o(x2)
助记自我检测:
sinx cosx arcsinx tanx arctanx
ln(1+x) ex (1+x)a
四.抓大头
无穷大吸收低次无穷大,无穷小吸收高次无穷小
五.夹逼准则及夹逼准则推出的两个重要极限
两个重要极限(写一个得了,简单的不写了):
lim
狗
→
∞
(
1
+
1
狗
)
狗
=
e
\lim \limits_{狗\rightarrow ∞}\left(1 + \frac{1}{狗}\right)^{狗} = e
狗→∞lim(1+狗1)狗=e
3.2 七种未定式的计算
常见的7种未定式:
0/0,∞/∞,0*∞,∞-∞,∞0,00,1∞
这里常考的是0/0和1∞
未定式计算的第一步,确定未定式类型.然后根据不同类型,挑选不同的计算工具解决
0/0型
- 等价无穷小,泰勒公式
- 洛必达法则
∞/∞型
- 洛必达法则
- 分子分母同除最高阶的无穷大
0*∞型
- 化成0/0型或∞/∞型
∞-∞型
- 通分化成0/0(适用于分式差)
- 根式有理化(根式差)
- 提无穷因子,然后等价代换或变量代换,泰勒公式
1∞
- 改写成指数函数,用洛必达法则
- 凑基本极限,秒杀
关于第二种方法:
lim
u
→
1
,
v
→
∞
u
v
=
lim
u
→
1
,
v
→
∞
e
v
ln
u
=
lim
u
→
1
,
v
→
∞
e
v
(
u
−
1
)
\lim_{{u \to 1, v \to \infty}} u^v = \lim_{{u \to 1, v \to \infty}} e^{v \ln u} = \lim_{{u \to 1, v \to \infty}} e^{v(u-1)} \quad \text{}
u→1,v→∞limuv=u→1,v→∞limevlnu=u→1,v→∞limev(u−1)
∞0,00型
- 化成幂指函数
4.函数的连续和间断
4.1 基础知识
本质还是极限的计算,但是定义要深刻掌握
函数某点连续的定义:
函数在某点的邻域内有定义,且x→x0时,limf(x)=f(x0)
不连续就讨论间断呗,但是讨论间断的前提和连续是一样的,函数在某点的邻域内得有定义.
间断点:
第一类和第二类间断点:
第一类左右极限都存在,第二类至少有一边极限不存在.
第一类间断点
- 可去间断点:左右极限存在且相等,但是不等于该点函数值
- 跳跃间断点:左右极限存在且不相等
第二类间断点
- 无穷间断点:有一边极限是无穷
- 振荡间断点:有一边极限是振荡的
4.2 进阶知识
4.2.1 连续函数性质的推广
- 连续加减连续=连续
- 连续加减间断=间断
- 间断加减间断=不一定
3的解释说明
f(x)=0 x<0
=1 x≥0
g(x)=1 x<0
=0 x≥0
f(x)是间断的,g(x)也是间断的
但是g(x)+f(x)是常函数,是连续的
- 连续*连续=连续
- 连续➗连续且非零=连续
如果分母可以是0的,就没有定义了,自然不必讨论连续,是间断的了
- 连续➗连续且为零=间断
- 连续且非零*间断=间断
- 连续且为零*间断=不一定
- 间断*间断=不一定

![MySql性能调优04-[MySql事务与锁机制原理]](https://i-blog.csdnimg.cn/direct/ee3a2a3ecadc4e5eb330007d4184ee84.png)