文章目录
一、归并排序
递归法
思想
程序代码
时间复杂度
非递归法
思想
程序代码
二、快速排序(挖坑法)
思想
程序代码
时间复杂度
三、快速排序(hoare法)
思想
程序代码
hoare法错误集锦
死循环
越界
四、快速排序(前后指针法)
思想
程序代码
五、快速排序非递归法
思想
程序代码
一、归并排序
递归法
思想
试想一下,如果有这样一个序列 [ 6,7,8,9,10,1,2,3,4,5 ] ,现在对这个序列进行排序,用归并排序就是最好的方法。将数据看成两组 [ 6,7,8,9,10 ] 和 [ 1,2,3,4,5 ] ,设置两个指针分别指向两组的第一个数据,然后比较两个指针指向的数据,小的数据放到新数组里面,同时该组的指针后移一位。循环此过程,直到某一组数据移动完毕。这样另一组未移动完的数据是比新开数组里面的所有数据都大的,直接按顺序拷贝到新数组里面即可。此算法的前提就是,两个组别里面的数组必须是有序 且是 同样的顺序。
那么对于一个乱序数组,要使用归并排序排成有序数组,该怎么做呢?如下图,即是乱序,就不能保证向上面一样,直接分成两组是有序的,那么就要细分下去,直到分出的 两组里面,每一组都只有一个数据,一个数据自然是有序的,这种分下去的思想叫做“分治”。
然后像右图一样,首先是单个数据为一组,每两组数据做归并排序;第一次排好之后,之前的分别排序的两组数据,现在就是有序的,将其归为一组,则现在两个数据为一组且有序(黄色背景),每两组数据做归并排序;第二次排好之后,得到的是每4个数据有序的序列,那么分成两组,进行归并排序,最后完成。
程序代码
代码传入四个参数,分别是待排序数组,待排序数组首元素下标,待排序数组末元素下标,一个和待排序数组同样大小的数组(如果函数内部临时开辟,递归越深,占用堆区内存越多,这样不合适)。不难看出,先将数组递归下去,分成一个个 [ left,right ] 这样的,对每一个这样的数据进行归并排序,然后返回,进行一个个 [ left,left+1,left+2,right ] 这样数据的归并排序……直到排序结束,数组有序。
void MergeSort(int* p, int left, int right, int* ret)
{
if (left >= right) // 返回条件
return;
int mid = (left + right) >> 1;
//此时被分为 [left,mid] [mid+1,right]
MergeSort(p, left, mid, ret);
MergeSort(p, mid + 1, right, ret);//既然递归了,就得有返回条件
//开始排序
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;//index表示这次递归中要排序的开始数据的下标
while (begin1 <= end1 && begin2 <= end2)//两个都满足的情况下才进行排序
{
if (p[begin1] < p[begin2])
{
ret[index++] = p[begin1++];
}
else
ret[index++] = p[begin2++];
}
//有一组有剩余的情况
while (begin1 <= end1)
{
ret[index++] = p[begin1++];
}
while (begin2 <= end2)
{
ret[index++] = p[begin2++];
}
//ret只是暂时存放,最后还要放回p里面,才是排序完成
for (int i = left;i <= right;i++)
{
p[i] = ret[i];
}
}时间复杂度
O(N*log N) ,(2为底)。
非递归法
思想
递归法主要是依靠递归,将无序的整个序列一直细分下去,细分到每一小组只有一个元素,就能保证每个小组都是有序的,然后两个小组开始归并排序。但是,如果省略递归这个过程,直接从每一小组只有一个元素的情况开始归并排序,那就是非递归法。
但是,非递归法也存在一些问题。比如,不能保证每一次都可以凑齐要归并排序的两组数据。比如下图,在单个数据为一组的情况下(蓝色背景),前面四次归并都没有问题,到了第五次,发现只有一组数据;在两个数据为一组的情况下(黄色背景),也是,前两次归并没问题,第三次归并,只有左边那组有一个数据;在四个数据为一组的情况下(红色背景),第一次归并没问题,第二次归并也是,只有左边那组有一个数据;终于,到了八个数据为一组的情况,左边数据完整,右边那组只有一个数据,虽然右边数据不全,但是也可以进行归并排序,所以直接排序得到最终结果。从这个推导过程可以得出一个结论:遇到凑不齐两组数据的情况,只有当一组数据完整,另一组至少有一个数据,才可以开始归并排序,否则跳过。
程序代码
如下,只需要传入两个参数,待排序序列首元素指针、待排序序列大小。由于不使用递归方法,所以临时数组空间可以在函数内部开辟,不用传参。归并的过程和递归法一样,只是控制从一个数据为一组的情况开始排序,然后逐渐到两个数据为一组、四个数据为一组……最终排序结束。gap一开始无疑是1,进去之后,从左到右 以gap=1 开始排序;gap=1的情况结束,gap增长两倍,为2,然后从左到右以gap=2 开始排序……如此循环,直到gap>=n 的情况,就表示排好了。
//归并排序非递归
void MergeSortNoR(int* p, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
printf("malloc fail!");
exit(-1);
}
int gap = 1;//gap表示每一次归并,一组数据的数据个数
while (gap < n)
{
for (int i = 0;i < n;i += 2 * gap)
{
// [i,i+gap-1] [i+gap,i+2*gap-1] [i+2*gap ……
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//右半区间不存在,这个时候前面都排完了,然后左半区间本来就是有序的,所以进行下一轮即可
if (begin2 >= n)
{
break;
}
//左半区间八个值,但是右半区间值少于八个
if (end2 >= n)
{
end2 = n - 1;
}
//左半区间不够gap个,这个不够gap区间的内容本来就是有序的,所以不用拷回去,直接拷贝到前一个end2的内容就可以
//必须要是拷贝到end2,因为上面几行end2可能被修正过,右半区间少了,不能拷贝到i+2*gap-1的内容
int index = i;//temp这个数组要存的内容的下标
//开始归并
while (begin1 <= end1 && begin2 <= end2)
{
if (p[begin1] <= p[begin2])
{
temp[index++] = p[begin1++];
}
else
{
temp[index++] = p[begin2++];
}
}
while (begin1 <= end1)
{
temp[index++] = p[begin1++];
}
while (begin2 <= end2)
{
temp[index++] = p[begin2++];
}
for (int j = i;j <= end2;j++)
{
p[j] = temp[j];
}
}
gap *= 2;
}
free(temp);
}二、快速排序(挖坑法)
思想
快速排序和归并排序有点类似于是反着来的。归并排序是先递归分成小块,从小块开始排序,逐渐排大块的;快速排序是先排大块的,然后递归下去排小块。
如下图,左边是归并排序和快速排序的差别(大体上而言),右边是快速排序举例。可能觉得 [ 6,1,2,9,10,4] 这个序列里的数据少了,那么如果初始序列是这样 [ 10 , 20 ,15 , 6 , 1 ,17, 31 , 4 , 40 , 9 , 2, 25 ] ,这几个数字选取一个大小适中的数字,15(绿色背景),然后比它小的数据 10,6,1,4,9,2 ,经过第一轮会被放在15 的左边(但是顺序不一定是我列出来的这样),然后进行下图右边排序,也是一样的,最后可以排出正确的升序序列。同理, 经过第一轮被放在 15 右边的 20,17,31,40,25 也可以排成升序序列,然后初始序列就是升序的。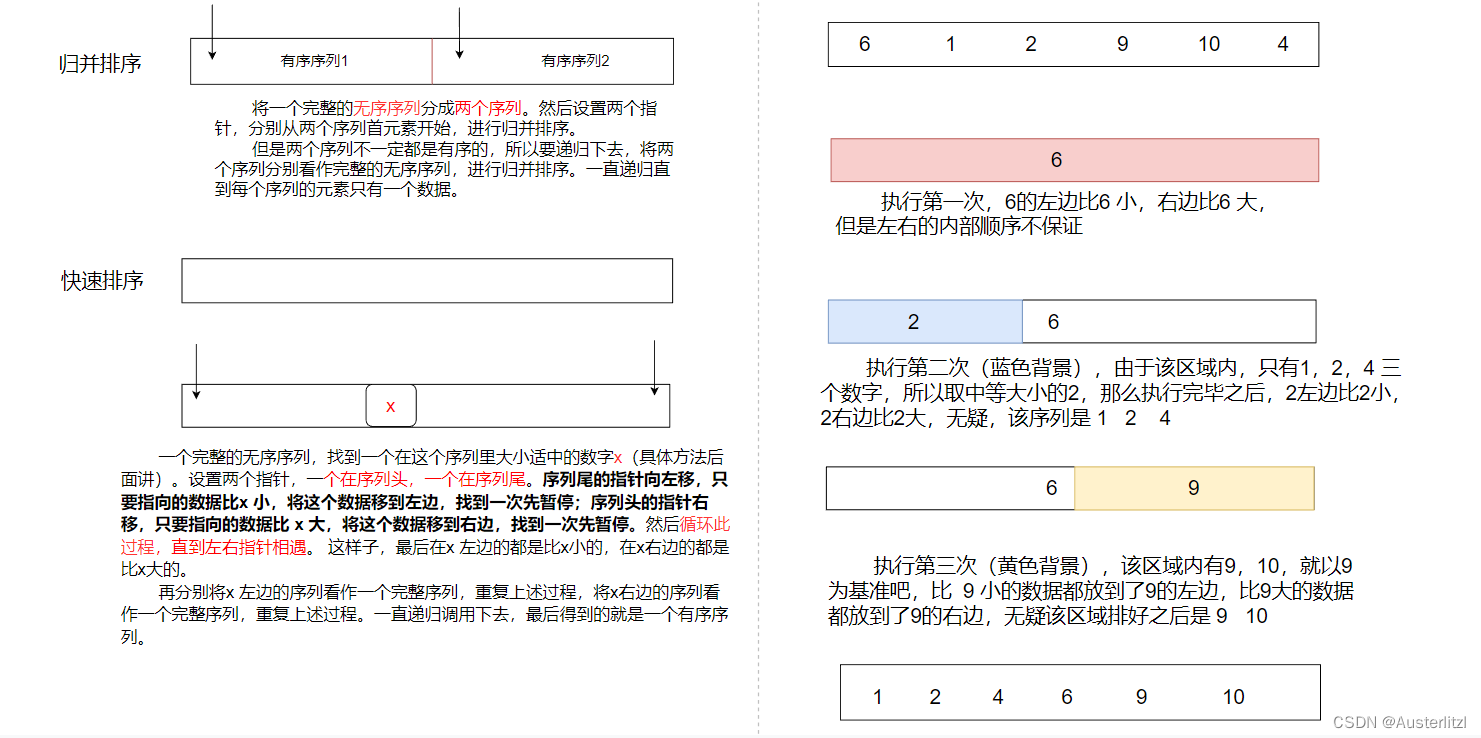
由此可以看出,快速排序是可行的,从宏观上而言,每次都找到了一个适中的数据,并且保证比它小的都在它的左边,比它大的都在它的右边,那么从细节方面,我们如何去实现这种排序呢?如下图,这是使用挖坑法进行快速排序的其中一段过程,假设这里所取的适中数字是10:
可是,上图最开始的左边指针为什么会是“坑” 呢?最开始这个“坑” 从何而来?一个数组总不可能凭空多出一个“坑” ,其实,我们一开始是把整个序列第一个数字当作“坑” 。
有一个乱序序列,进行快速排序。
第一轮,首先用三数取中法确定适中的数字。三数取中法就是,将待排序序列的 首、尾、中间 这三个位置的数据里面取出中等大小的数据 x 。
将这个中等大小的数据 x 和首位的数据交换,然后开一个变量 temp 存储这个中等大小的数据。
将首位 x (现在是选出的中等大小的数据)当作坑,序列尾的指针先开始找数据,只要找到比 x 小的数据,就放到坑里面,然后右边指针指向的位置变成了坑;然后序列头的指针右移,找比 x 大的数据,放到右边的坑里面,同时左边指针指向的位置也变成了坑。

知道了这个过程,也就知道这个所谓的“坑” 是怎么来的了,但是,最后如何将这个中等大小的数据放回数组里面呢?上面提到,会开一个 temp 来存储这个中等大小的数据,所以现在的问题就是,将它放在哪里?
如下图,我们假设现在右边的指针指向坑,那么就是左边的指针在寻找比 x 大的数据,然后经过数据都比 x 小,直到两个指针相遇,那么两个指针共同指向坑位。此时,由于当前坑位左边,指针都走过一遍了,所以数据都是比 x 小的; 对于当前坑位右边,指针也走过一遍了,所以数据都是比 x 大的。那么,当前坑位自然就是最适合存放 x 的地方。反过来,如果左边指针指向坑,右边指针走过来都遇到比 x 大的数据,直到两个指针相遇,那么也是同样的,当前坑是最适合存放x 的地方。所以左边指针移动遇到右边指针,还是右边指针移动遇到左边指针,都一样。
程序代码
如下,是三数取中法 和 快速排序的代码,快速排序里面开了四个变量,begin、end、pit、temp,分别代表着 左边指针、右边指针、坑位、存放三数取中法得到的数据。虽然坑位肯定是左右指针中的一个,但是程序无法自动判断哪一个是坑位,所以直接用一个指针来当作坑位,坑位变了就把 pit 指针指向坑位。
在最后,有使用到插入排序。这样操作的原因是,如果要对一个很长的无序序列进行快速排序,那么最后肯定要细分成很多一小段一小段的独立序列,这个时候递归的层次就很深,需要递归很多次,非常占用资源,而且也有栈溢出的风险。所以,不如递归到每一个序列只有十个左右数据的时候,直接使用插入排序一次搞定,不需要递归下去了。
int* GetMidIndex(int* a, int* left, int* right)
{
int* mid = left + (right - left) / 2;
if (*left < *mid)
{
if (*mid < *right)
{
return mid;
}
if (*left > *right)
{
return left;
}
else
return right;
}
else// *mid<*left
{
if (*left < *right)
{
return left;
}
if (*right < *mid)
{
return mid;
}
else
return right;
}
}
void QuickSort(int* p, int* left, int* right)
{
if (left > right)//递归终止条件
{
return;
}
//用三数取中法要把取到的数和首元素交换
int* Index = GetMidIndex(p, left, right);
Swap(left, Index);
int* begin = left;
int* end = right;
int* pit = begin; // pit是坑位,最开始是默认最左边
int temp = *begin; // temp存放三数取中法得到的数据
while (begin < end)
{
while (begin < end && *end >= temp)
{
end--;
}
*pit = *end;
pit = end;
while (begin < end && *begin <= temp)
{
begin++;
}
*pit = *begin;
pit = begin;
}
*begin = temp;
pit = begin;
//现在区间被分为了 [left,pit-1] pit [pit+1,right]
//但是在这里如果直接递归的话,到最后只剩下比如10个数据,那么要递归很多很多次,不如最后的数据直接用其他办法排序
//小区间优化法:
if (pit - 1 - left > 10)
{
QuickSort(p, left, pit - 1);
}
else
InsertSort(left, pit - 1 - left + 1);//左区间开始插入排序
if (right - pit - 1 > 10)
{
QuickSort(p, pit + 1, right);
}
else
InsertSort(pit + 1, right - pit - 1 + 1);//右区间开始插入排序
}三、快速排序(hoare法)
思想
和挖坑法类似,如果要排升序,其单趟操作也是找出一个适中的数据 x ,单趟操作结束之后,比 x 小的都放在了 x 的左边,比 x 大的都放在了 x 的右边。如下图:
我们再来看一看单趟排序是如何操作的:首先要找出一个当前序列里面,大小适中的数字,也是三数取中法,将该数字放到序列首位。然后设置两个指针,分别指向当前序列的首、尾。尾部指针先向左移动,找到比 x 小的数据停下来; 首位的指针向右移动,找到比 x 大的数据停下来;此时交换两个指针指向的数据。接着重复执行绿色背景的操作,直到两个指针相遇,交换相遇位置的数据和序列首位的数据。如下图:
对于上述过程可能有人会问,两个指针相遇处的数据,难道不会比 6 大吗?为什么就这样直接交换了呢?我们可以把指针相遇分为两种情况:第一,右指针遇到做指针;第二左指针遇到右指针。
对于第一钟情况,上图已经给出详细过程,因为每一轮都是右边指针先开始向左移动,所以,如果是右边指针遇到左边指针,一定是上一轮结束(此时数据已经交换,左边指针指向的是比6 小的数据,右边指针指向的是比 6 大的数据),接着右边指针直接开始移动,遇到左边指针,那么两个指针指向的就是比 6 小的数据,可参考上图。
对于第二种情况,如果是左边指针遇到右边指针,由于每一轮是右边指针先移动,所以肯定是右边指针找到了比 x 小的数据,然后左边指针开始移动,遇到右边指针了,两个指针相遇,指向的是这一轮中,右边指针找到的数据,那肯定是比 x 小。
所以,无论是左边指针遇到右边指针,还是右边指针遇到左边指针,都一样,两个指针都是同时指向比 x 小的数据。(当然,如果改成每一轮都是左边指针先走,右边指针后走,那么结果就是截然不同,可以尝试画图。)
每一趟再递归下去,就可以得到最后的结果,其递归过程就和二叉树的过程类似。如下图,详细的递归展开图就不展示了,和二叉树遍历基本一样的。
程序代码
如下,三数取中法代码在挖坑法那里有,就不展示了。最下面的代码也是同理,如果遇到序列里的元素个数比较少,就不要递归下去了,不然递归层次太深。
void QuickSort2(int* p, int* left, int* right)
{
if (left >= right)//递归终止条件
return;
int* index = GetMidIndex(p, left, right);
Swap(index, left);
int* begin = left;
int* end = right;
int* pit = begin;
while (begin < end)
{
while (begin < end && *end >= *pit)
{
end--;
}
while (begin < end && *begin <= *pit)
{
begin++;
}
Swap(begin, end);
}
Swap(pit, begin);//交换相遇处的和开始的
//被分成了 [left,begin -1] begin [begin+1,right]
if (begin - 1 - left + 1 > 10)
{
QuickSort2(p, left, begin - 1);
}
else
InsertSort(left, begin - 1 - left + 1);
if (right - begin - 1 + 1 > 10)
{
QuickSort2(p, begin + 1, right);
}
else
InsertSort(begin + 1, right - begin - 1 + 1);
}hoare法错误集锦
使用hoare法,很容易掉进“坑”里面,这里的“坑”主要有两个:一是容易造成死循环;二是容易产生越界。这些坑必然是单趟排序的代码错误造成的,所以我们主要看while循环里面的代码。
死循环
while (begin < end)
{
while (*end > *pit)
{
end--;
}
while (*begin < *pit)
{
begin++;
}
Swap(begin, end);
} 如上,如果像这样子写,外部的while( begin < end) 循环控制条件自然没有什么问题,只要跳出循环就是相遇了。但是对于其内部while()的循环控制条件,假设本轮三数取中确定的数字是 x ,首先执行第第一个while(), 如果 右边指针遇到 *end = *pit(即右边的指针指向的数字 等于 x ) 的情况,自然也停下来了,因为不满足循环控制条件; 接着指向第二个while(),*begin < *pit 的情况下(即左边指针指向的数据小于 x ),左边指针才会++ ,但是序列首位就是 x ,所以左边指针无法++。然后交换左右指针指向的数据,交换完都指向 x ,左右指针无论如何都无法继续移动,死循环。
那么如何改进呢?很简单,只需要更改内部循环控制条件,把等于 x 的数据过滤掉,不去管他。在进行下一轮递归处理的时候,自然会处理被过滤的 x 。如下,本轮三数取中确定的 x 是6,但是序列中有另外两个数据等于 6,不需要管,直接跳过,后面的递归调用(红色、蓝色背景区域)自然会处理其余的 6 。
如下,可以解决死循环的问题,遇到等于 x 的值,直接跳过。
while (begin < end)
{
while (*end >= *pit)
{
end--;
}
while (*begin <= *pit)
{
begin++;
}
Swap(begin, end);
}越界
那么,越界问题又是如何产生的呢?如下,在不考虑三数取中法的情况下,如果选取的 x 值是1,是整个序列里面最小的,当右边的指针往左边移动的时候,找到的全是比 1 大的,最后移到和左边指针同样的位置,由于上面的条件,遇到1直接过滤了,所以依然无法停下来,就会导致越界。

所以,如下,不光要在外部while 检测,也要在内部while检测 begin<end 。 当然,也可以这样子理解:当外部while 条件满足的时候,进入循环确实是 begin < end ,但是如果内部while不检测,那么经过内部begin、end 指针的移动,也不知道是否还满足 begin<end ,所以内部的while循环必须也要检测。
while (begin < end)
{
while (begin<end && *end >= *pit)
{
end--;
}
while (begin<end && *begin <= *pit)
{
begin++;
}
Swap(begin, end);
}四、快速排序(前后指针法)
思想
三数取中得到 x ,然后将 x 放到首位,设计两个指针prev,cur,一开始 prev 指向序列第一个数据,cur指向第二个,然后cur一直要++,直到碰到比 x 小的,那么prev++,然后交换两个指针指向的数据。最后 cur 指针越界,交换序列第一个数据和 cur 指针指向的数据。递归下去之前的过程,最后得到的就是升序序列。(降序序列只需要反过来,cur 遇到比*pit 大的就交换)
如下,一次下来,6左边的都比6小,右边的都比6大。排好这一次之后,再递归下去,排一个个小区间,直到结束,排序完成。
这个方法可以总结出一点点小规律,那就是,prev指针所过之处,全部都是比 x 小的值,包括 prev 指针本身(除去序列首位)。因为只有 cur 指针找到了 比 x 小的数据,然后 prev 才会前移一个位置 ,交换两个指针的值,所以才会有这个规律。
程序代码
如下代码,其中while循环里,巧妙之处就在于 if (*cur < *pit && ++prev != cur) 。如果一个序列是:6 8 2 3 0 ,prev指向6,cur指向8,此时*cur > *pit,那么&&左边的逻辑值就是0,根据&&符号的规则,不会执行右边,prev也就不会++ 。如果 && 左右两边的表达式交换位置,那么无论是否需要交换 prev 和 cur 指向的值,prev 指针都要++,就会出错。
void QuickSort3(int* p, int* left, int* right)
{
int* index = GetMidIndex(p, left, right);
Swap(index, left);
int* prev = left;
int* cur = left + 1;
int* pit = left;
while (cur <= right)
{
//只要cur指向的比*pit小,prev就会++,确保prev经过的都是比*pit小的
if (*cur < *pit
&& ++prev != cur) // ++prev==cur的情况下,那么就没有必要交换,因为两个一样
{
Swap(prev, cur);
}
cur++;
}
Swap(pit, prev);
//现在分成了[left,prev-1] prev [prev+1,right]
if (prev - 1 - left + 1 > 10)
{
QuickSort3(p, left, prev - 1);
}
else
InsertSort(left, prev - 1 - left + 1);
if (right - prev - 1 + 1 > 10)
{
QuickSort3(p, prev + 1, right);
}
else
InsertSort(prev + 1, right - prev - 1 + 1);
}五、快速排序非递归法
思想
不像归并排序,先递归分成最小序列,再由小序列到大序列 排序;快速排序必须要由大序列排到小序列。所以,快速排序非递归的方法较为难以理解——在这里要引入 栈 来帮助进行排序。
如下这张简略的快排递归展开图,数字序号就是对应的执行顺序。首先排完最长序列之后,并不是先排左边序列,再排右边序列,然后再排下面的小序列;而是先排左边序列(序号1),然后一条路走到黑,每次都排更小的序列(序号2),直到不能再排(3、4、5),再返回排稍微大一点的序列(6),直到左边排完了,再开始右边(7),右边也和左边一样的。

我们可以利用栈,首先将最大的序列进行一次排序,排好了将左右两个子序列放到栈里面;取出栈里面的数据,排一个子序列,这个子序列一次排序完成,又将该子序列的左右子序列放到栈里面(有就放、没有就不放)……一直这样循环,直到栈没有数据了,就排好序了。注意,每次放左右子序列的先后顺序是一样的,要么就一直先左后右,要么就一直先右后左。
如下图,上方是递归过程对各序列编号,有助于理解。下方是利用栈进行排序的过程,每一次排序的核心代码是没有改变的,其结果也依然是 x 左边的都比 x 小,x右边的都比 x 大。只是非递归法是利用栈而已。
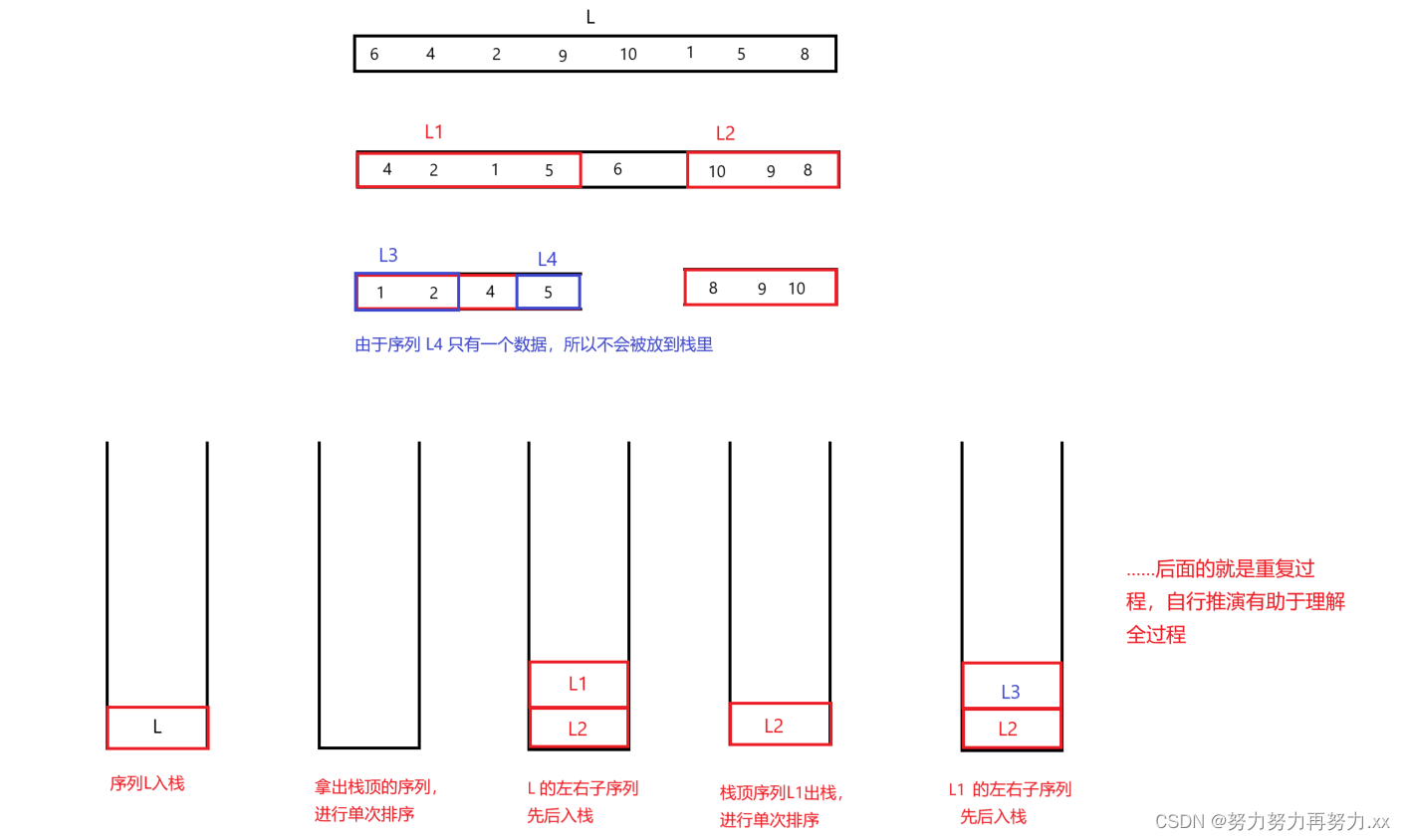
通过理解利用栈的过程,也可以明白,其实每一个序列先后执行顺序和递归法是一样的,可以对比参考快排简略的递归展开图。非递归法其实就是利用栈后进先出的特点,先将右子序列压倒最底下,然后一直执行左子序列及其子序列等等的单次排序,直到排完,再进行右子序列的同样顺序的单次排序。
程序代码
如下,第一个函数 PartSort 是对每一个序列进行排序的过程,和上面三种递归方法的区别就是,没有递归(有点绕.....)。第二个函数 QuickSortNoR 就是利用栈进行快速排序的过程,每一次对一个序列快排都要利用PartSort。
int PartSort(int* p, int left, int right)
{
int* temp = GetMidIndex(p, p + left, p + right);
Swap(temp, p + left);//之前一直出错,就是这里交换的是p和temp,应该交换p+left,每次快排区间的第一个值
int begin = left;
int end = right;
int pit = begin;
int temp1 = p[left];//要比较的值,是每次比较区间的首位,而不是整个数组的首位
while (begin < end)
{
while (begin < end && p[end] >= temp1)
{
end--;
}
p[pit] = p[end];
pit = end;
while (begin < end && p[begin] <= temp1)
{
begin++;
}
p[pit] = p[begin];
pit = begin;
}
pit = begin;
p[pit] = temp1;
return pit;
}
void QuickSortNoR(int* p, int n)
{
ST st;
StackInit(&st);
StackPush(&st, n - 1);
StackPush(&st, 0);
while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
int KeyIndex = PartSort(p, left, right);//一方面,排序,另一方面,找到当此排序的那个数的位置
//[left KeyIndex-1] KeyIndex [KeyIndex+1,right]
if (KeyIndex + 1 < right)
{
StackPush(&st, right);
StackPush(&st, KeyIndex + 1);
}
if (KeyIndex - 1 > left)
{
StackPush(&st, KeyIndex - 1);
StackPush(&st, left);
}
}
}以上就是快排和归并排序的递归法以及非递归法,呕心沥血之作,希望多多支持,有错误的地方也欢迎评论区指正!