一、激活函数的提出
1. Motivation
通用逼近定理(Universal Approximation Theorem):一个包含单一隐含层的多层神经元网络能够以任何期望的精度近似任何连续函数。
构建神经网络的核心目的是拟合函数,通过前向传播得到拟合函数或者判别函数输出最终的结果,最初的神经网络的前向传播思想非常简单,即线性变换。然而,如果仅仅通过这个过程,无论中间包含多少层隐藏层,最终得到的函数仍然是线性的,无法构建出非线性的拟合函数,这就引出了激活函数。
换言之,如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
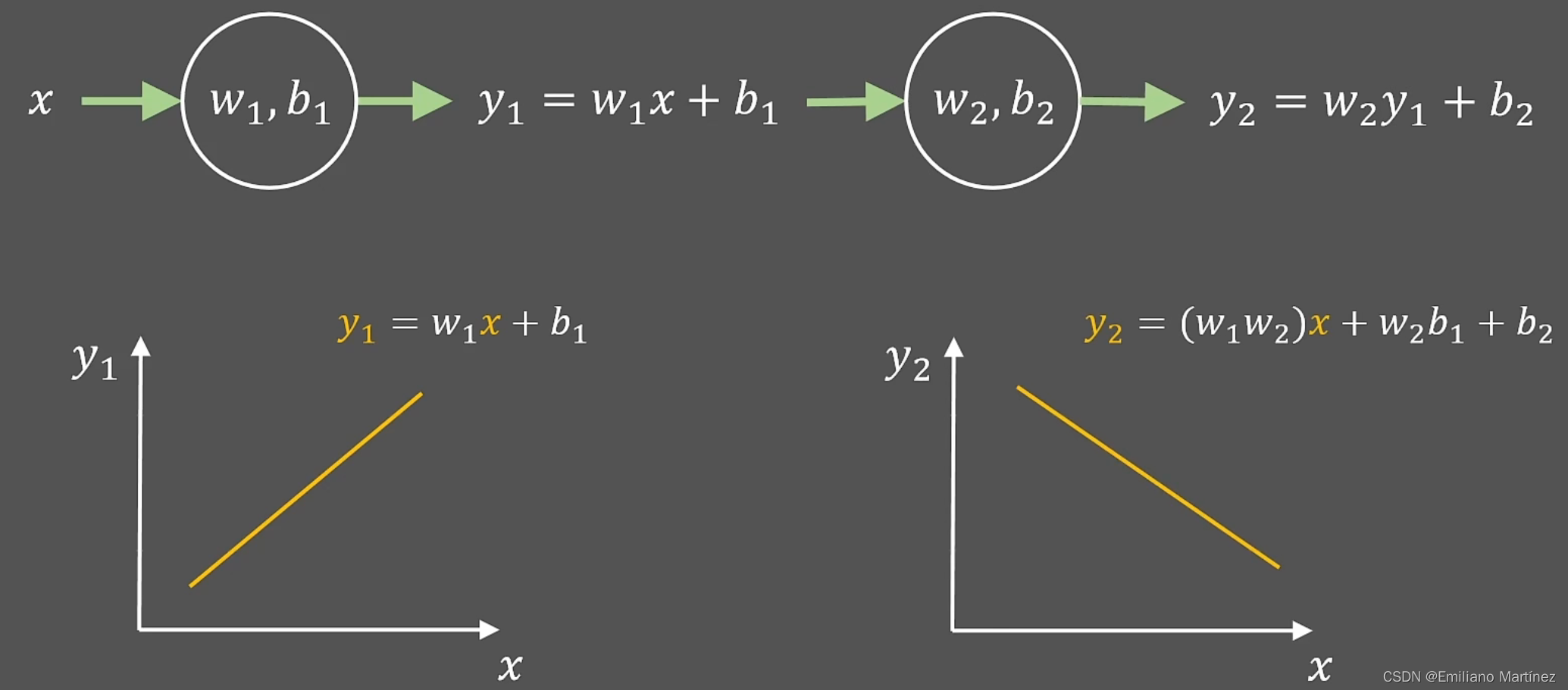
2. 激活函数的基本性质
(1)连续可导函数
由于激活函数也要参与反向传播,因此要求激活函数必须是连续可导的函数。