逻辑运算及其基本概念,定理,算法,规律,卡诺图
文章目录
- 逻辑运算及其基本概念,定理,算法,规律,卡诺图
- 开胃小菜
- `运算`
- `1、与运算`
- `2、或运算`
- `3、非运算`
- `4、与非(都1时为0)`
- `5、或非(都0时为1)`
- `6、异或(同为0,异为1)`
- `7、同或(同为1,异为0)`
- `定理和规则`
- `吸收律(对偶规则)`
- `反演律(摩根定理)`
- ` 恒等式`
- `反演规律`
- `对偶规则`
- `最小项与最大项`
- `最小项与最小项表达式`
- `最大项与最大项表达式`
- `最小项和最大项的关系`
- `卡诺图化简法`
- `概念`
- `化简详解`
- `步骤`
- `画包围圈原则`
- `例1:充分体现【画包围圈的原则(2)】`
- `例2:【给出两种解法,圈1/圈0】`
- `具有无关项的化简`
- `如果对你有帮助,就点赞收藏把!(。・ω・。)ノ♡`
开胃小菜

概念:当0和1表示逻辑状态时,两个二进制数码按照某种指定的因果关系进行的运算称为逻辑运算。
逻辑运算与算术运算完全不同,它所使用的数学工具是逻辑代数(又称为布尔代数)。
逻辑变量只有两个可取的值,即0和1,表示完全对立的逻辑状态,因而称为二值逻辑变量。
运算
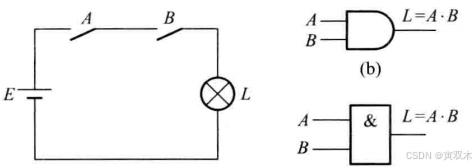
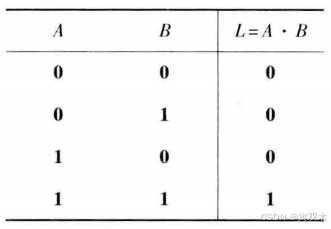
1、与运算
运算符: " · "
2、或运算
运算符: " + "
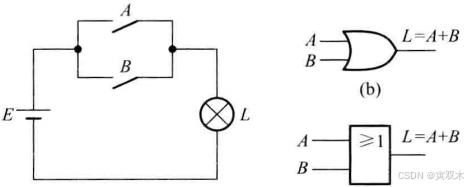
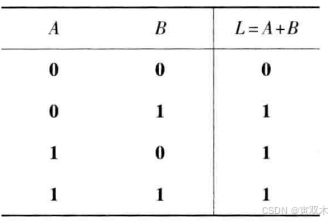
3、非运算
运算符: 字母上方的短线 " - " 表示非运算
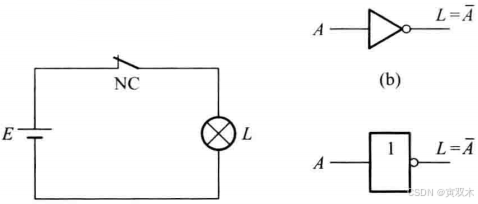
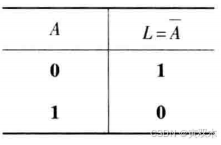
4、与非(都1时为0)
与非运算 是 与运算 和 非运算 的组合

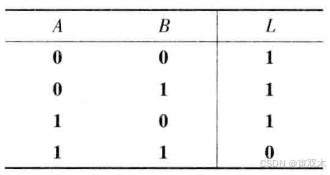
5、或非(都0时为1)
或非运算 是 或运算 和 非运算 的组合
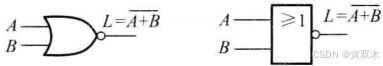
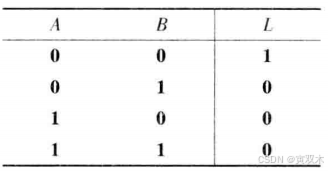
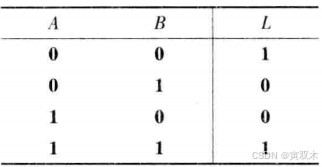
6、异或(同为0,异为1)

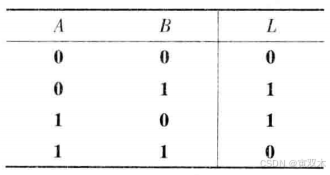
7、同或(同为1,异为0)

定理和规则
交换律,结合律,分配律等就不多赘述了
吸收律(对偶规则)

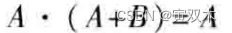
反演律(摩根定理)
经常用于求一个原函数的 非函数 或者 对逻辑函数 进行变换
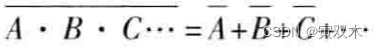
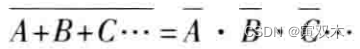
恒等式
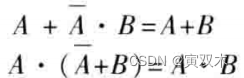
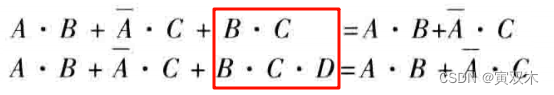
证明:(以第一个为例)

反演规律
定义:(摩根定理)
当需要由 原函数 𝐿 的表达式,求 它的非函数 时
只需要可以将 𝐿 中的
与( · ) 换成 或( + ),
或( + ) 换成 与( · ):
原变量 换为 非变量
非变量 换为 原变量
1换成0
0换成1
那么所得的逻辑函数式就是原函数 𝐿 的非函数 。
例如:
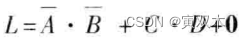
按照反演规则,得
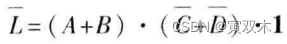
对偶规则
逻辑表达式 𝐿 ,若把 𝐿 中的 “与、或互换,0、1互换 ”,得到新的逻辑函数式,便是L的对偶式,记作 𝐿’
变换时需注意保持原式中 “先括号、然后与、最后或” 的运算顺序。
对偶规则为:当某个逻辑表达式相等,则它们的对偶式也相等
对偶性意味着逻辑代数中每个逻辑恒等式可以用两种不同的表达式进行表示。
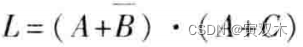
按照对偶规则,得
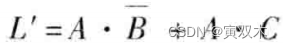
最小项与最大项
最小项与最小项表达式
对于有n个变量的逻辑函数,若有一个 与项(乘积项) 包含了全部的n个变量,
每个变量都以它的 原变量 或 非变量 的形式在乘积项中出现,
每个变量都出现 且 仅出现一次 ,则称该乘积项为 最小项 。
由若干最小项 相或 构成的逻辑表达式称为 最小项表达式 ,也称为 标准与-或表达式。
性质:
(1)任意一个最小项,只有一组取值使其值为1,而其他各组取值均为0。最小项不同,使其值为1的取值也不同
(2)任意两个不同的最小项之积为0(相与)
(3)所有最小项之和为1(相或)
最大项与最大项表达式
对于有n个变量的函数来说,若有一个 或项 包含了全部的n个变量,
每个变量都以它的 原变量 或 非变量 的形式在或项中出现,
每个变量都出现 且 仅出现一次 ,则称该或项为 最大项。
性质:
(1)任意一个最大项,只有一组取值使得值为0,而其他各组值是1。最大项不同,使其值为0的取值也不同
(2)任意两个不同的最大项之和为1(相与)
(3)所有最大项之积为0(相或)
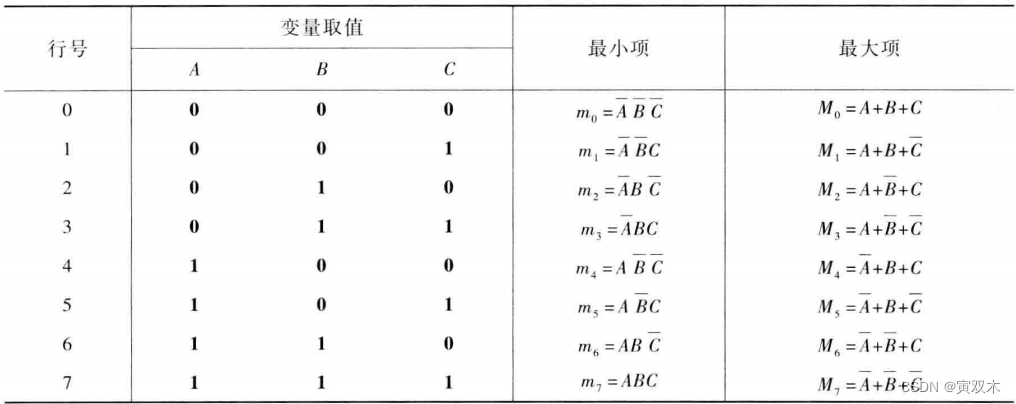
下标:
一般n个变量的最大项应有2^n个。最大项通常用Mi表示,下标编号 i 用于区别不同的最大项。
由性质(1)得出的这组取值,其对应的二进制数,所对应的十进制数,就是该最大项的下标编号。
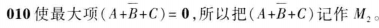
最小项和最大项的关系
根据最小项和最大项的性质可知,相同变量 构成的最小项与最大项之间存在 互补关系
卡诺图化简法
概念
卡诺图:逻辑函数的卡诺图就是将此函数的 最小项表达式 中的各 最小项 相应地填人一个特定的方格图内,此方格图称为卡诺图
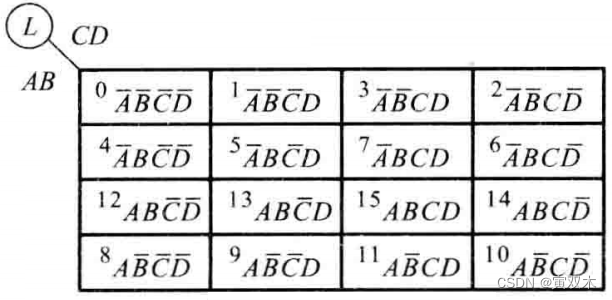
卡诺图的简化表示:
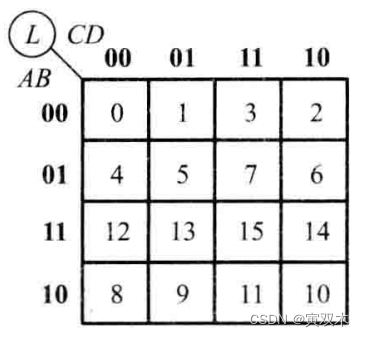
化简详解
步骤
(1)将逻辑函数写成最小项表达式。
(2)按最小项表达式填卡诺图,凡式中包含了的最小项,其对应方格填1,其余方格填0。
(3)找出为1的相邻最小项,用线画一个包围圈,每个包围圈含2^n个方格,写出每个包围圈的乘积项。
(4)将所有包围圈对应的乘积项相加。
(真值表 可以直接 填卡诺图,以上的(1)(2)两步就合为一步。)
画包围圈原则
(1)包围圈内的方格数必定是 2^n 个(偶数个),n等于0、1、2、3……。
(2)相邻方格包括 上下底相邻 ,左右边相邻 和 四个角两两相邻 。
(3)同一方格可以被不同的包围圈重复包围,但新增包围圈中一定要有新的方格,否则该包围圈为多余。
(4)包围圈内的 方格数要尽可能多 ,包围圈的 数目要尽可能少 。
化简逻辑函数后,一个包围圈对应一个乘积项,
包围圈越大,所得乘积项中的变量越少。
包围圈个数越少,乘积项个数也越少,得到的 与-或表达式 也最简。
例1:充分体现【画包围圈的原则(2)】
𝐿(A,B,C,D)=∑m(0,2,5,7,8,10,13,15),用卡诺图法化简逻辑函数,求 𝐿 的最简与-或表达式
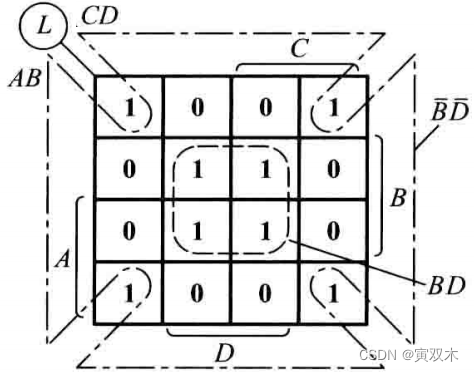
得出结果:
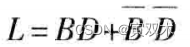
例2:【给出两种解法,圈1/圈0】
化简逻辑函数 𝐿(A,B,C,D) = ∑m(0~3,5 ~ 11,13 ~ 15)
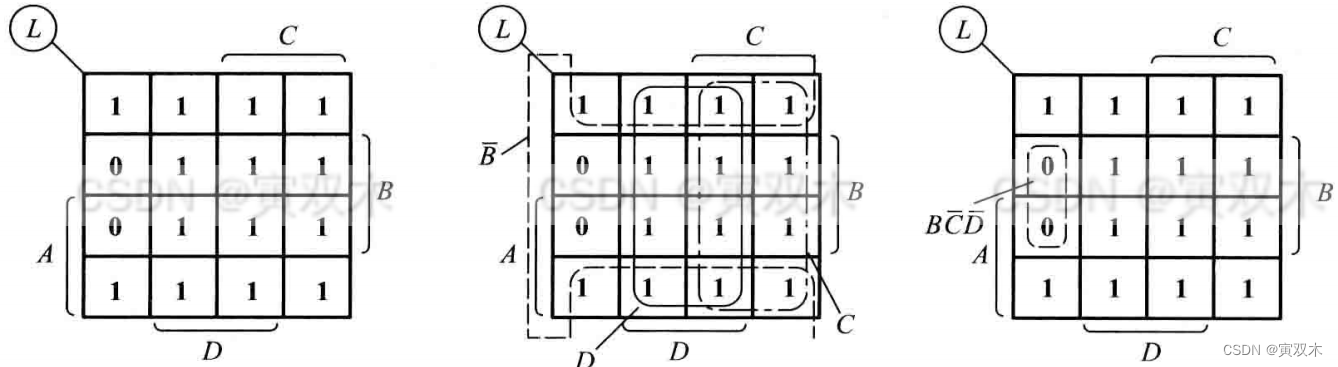
左图为 𝐿 的卡诺图,中图为圈1解法,右图为圈0解法
法1:用 包围1 的方法化简,得
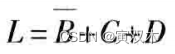
法2:用 包围0 的方法化简,得
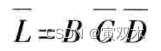
由摩根定理得

具有无关项的化简
在实际工作中,当逻辑变量被赋予特定含义时,有一些变量的取值组合根本就不会出现,或者对应于变量的某些取值
其函数值可以是任意的(它的值可以取0或取1),将变量取这些值所对应的最小项称为 无关项 或 任意项。
举例说明:
设计一个逻辑电路,判断 1位 十进制数是奇数还是偶数,当十进制数为奇数时,电路输出为1;当十进制数为偶数时,电路输出为0。
1位十进制数只有10个数,而卡诺图有16个数,那么多余的6个数就是 无关项 或 任意项
列出真值表:
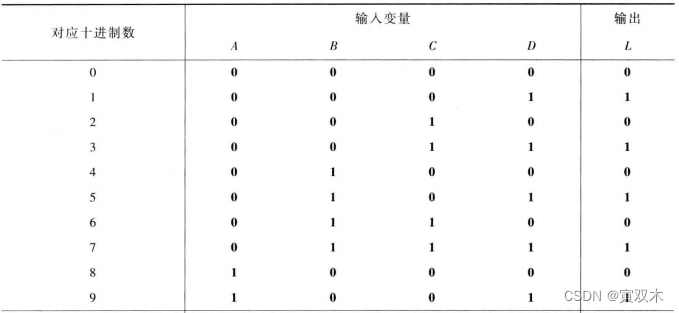
卡诺图如下:
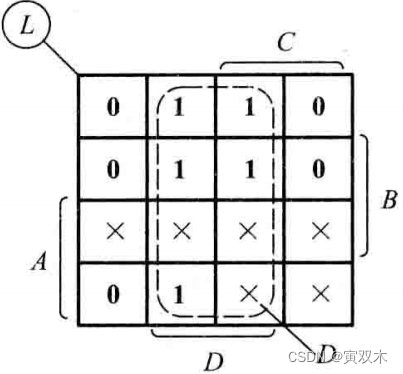
其中,无关项的函数值可以是任意的(它的值可以取0或取1)
如果不利用无关项,则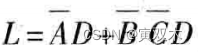
而如果13,15,11位置取1,逻辑表达式就化简成了
┈┈┈┈▕▔╲┈┈┈┈┈┈┈ ┈┈┈┈▕▔╲┈┈┈┈┈┈┈ ┈┈┈┈▕▔╲┈┈┈┈┈┈┈┈
┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈
┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈
▂▂▂▂╱┈┈▕▂▂▂▂▏┈ ▂▂▂▂╱┈┈▕▂▂▂▂▏┈ ▂▂▂▂╱┈┈▕▂▂▂▂▏┈┈
▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈
▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈
▔▔▔▔╲▂▂▕▂▂▂▂▏┈ ▔▔▔▔╲▂▂▕▂▂▂▂▏┈ ▔▔▔▔╲▂▂▕▂▂▂▂▏┈┈