文章目录
- 前言
- 向量数据库介绍
- 索引方法
- 倒排索引
- KNN 搜索
- 近似 KNN 搜索
- Product Quantization(PQ)
- NSW 算法搜索
- HNSW
前言
向量数据库是当今大模型知识库检索落地实践的核心组件,下图是构建知识库检索的架构图: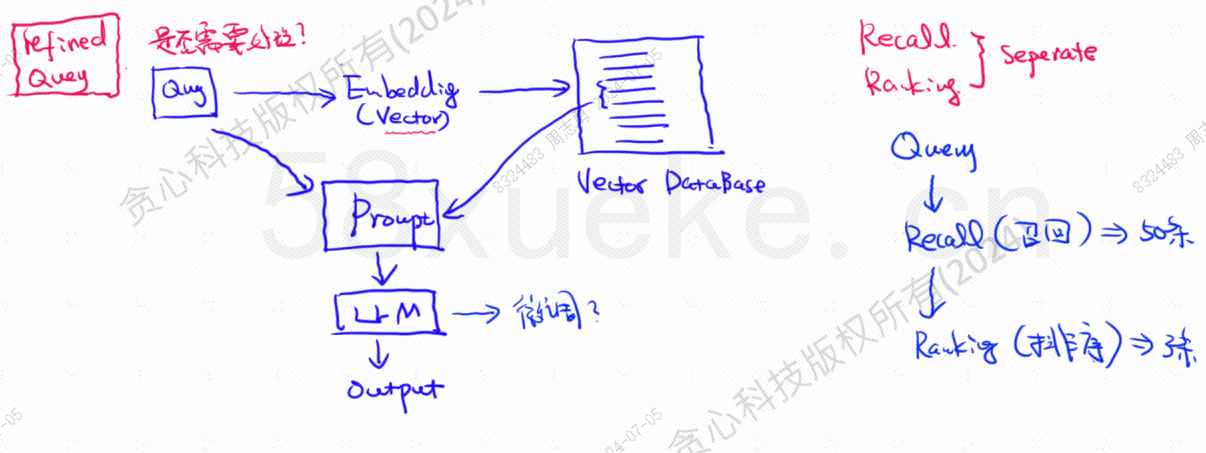
- 首先会将相关文档数据向量化嵌入到向量化数据库中,然后将用户的查询语句转为向量化查询,从向量数据库中召回相似度高的 TOP N 条数据。
- 然后在对这 TOP N 进行排序,取其中几条,构造成 prompt ,和 LLM 交互查询。
向量查询的数据与 query 的相似度,直接影响到 prompt 的好坏,本文将对市面上已有的向量数据库进行简单介绍,然后会对其使用到的索引方法进行说明,包括倒排索引,KNN,Approximate KNN, Product Quantization, HSNW 等,会对这些算法的设计理念和方法进行说明。
向量数据库介绍
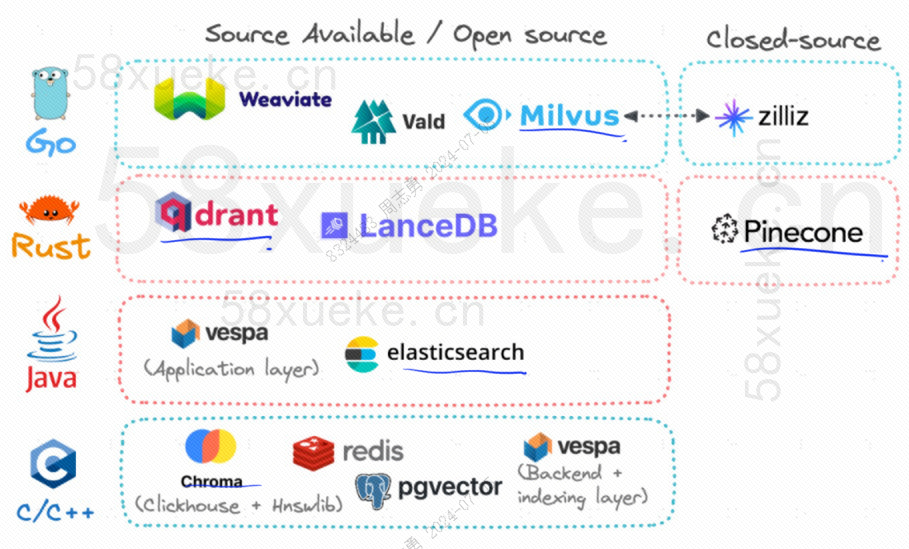
目前开源的比较火的三大向量数据库为 Chroma, Milvus, Weaviate,关于他们的介绍与区别这篇文章我觉得讲的不错,感兴趣的可以看下:三大开源向量数据库大比拼。
下边是开源向量数据库的发展历程: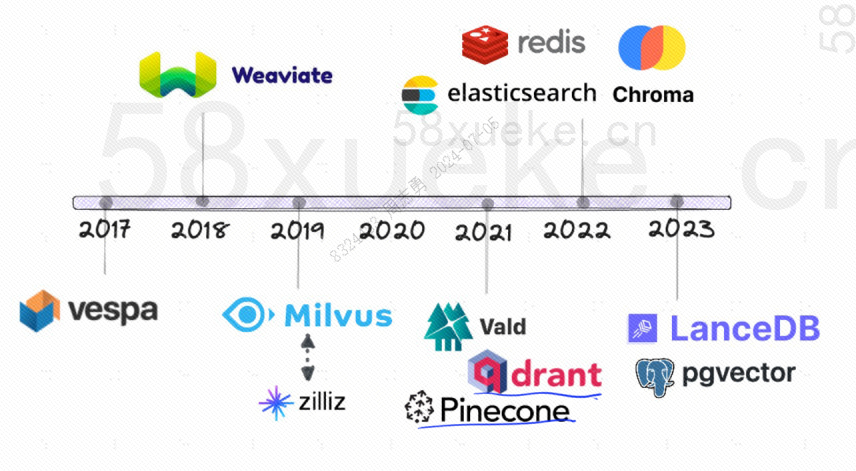
它们用到的索引方法如下:
索引方法
倒排索引

假如现在我有一个使用倒排索引的数据库,其中存储了10的12次方个索引数据,我们在往数据库中存储数据的时候,会将数据切分,然后记录被切分后的单词对应的索引位置有哪些, 因为不同句子可能会出现相同的单词,因此每个单词对应的是一个索引集合:
- 大模型——>[…]
- 应用——>[…]
- …
假设现在我有一个 query: 大模型的应用会在2024年有哪些发展?
数据库将我们的查询语句切分为三个关键单词:大模型,2024年,发展。然后查询出每个单词对应的索引结合,求交集,这一查询过程就叫做召回。
此时,我们就拿到了和查询相关联的数据,但是这些数据与查询语句相似度是不同的,我们需要对其进行排序,取 TOP N。
但是这种直接将文本数据和索引对应的查询效率并不高,我们有没有什么办法可以加速相似度检索呢?
这个时候就出现了向量化检索,将数据转化为向量,然后在通过计算向量的相似度和距离两方面来检索: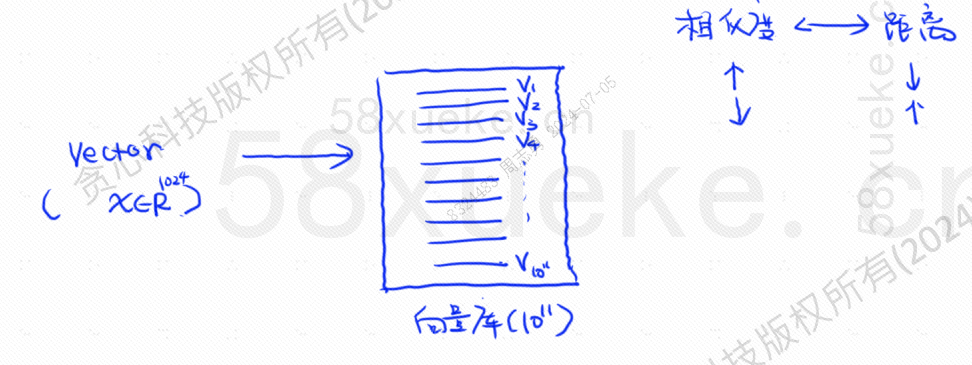
KNN 搜索
KNN 搜索叫做 K 近邻搜索,将查询语句转换为向量,然后再求该向量与数据库中的向量相似度最高,距离最近的向量集。
其中时间复杂度为O(N)*O(d), d 为维度,维度数据一般为固定的,假设数据库中存储了 10000个向量数据,其中维度都为 1024,那么查询出 maxSim(q,v)(相似度最高),minDist(q,v)(距离最近)的向量的时间复杂度就位 O(10000)*O(1024)。
这种检索方式的优点是查出来的数据精确度高,缺点就是慢。
近似 KNN 搜索
近似 KNN 搜索就是将搜索空间从点变为块,先确定距离最近的那一块,然后再在该快空间中寻找距离最近,相似度最高的点,下图中左边是KNN搜索,有边是 近似 KNN 搜索: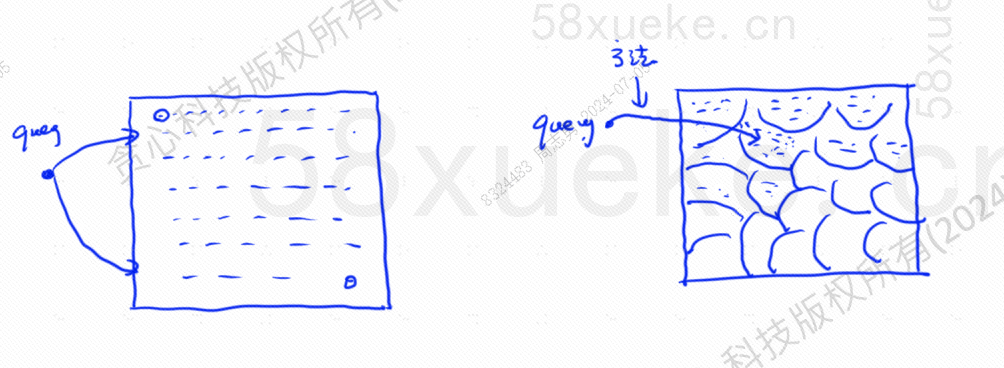
其中每个块中都会有一个中心点,计算查询点与块的距离就是计算查询点到每个块的中心点的距离: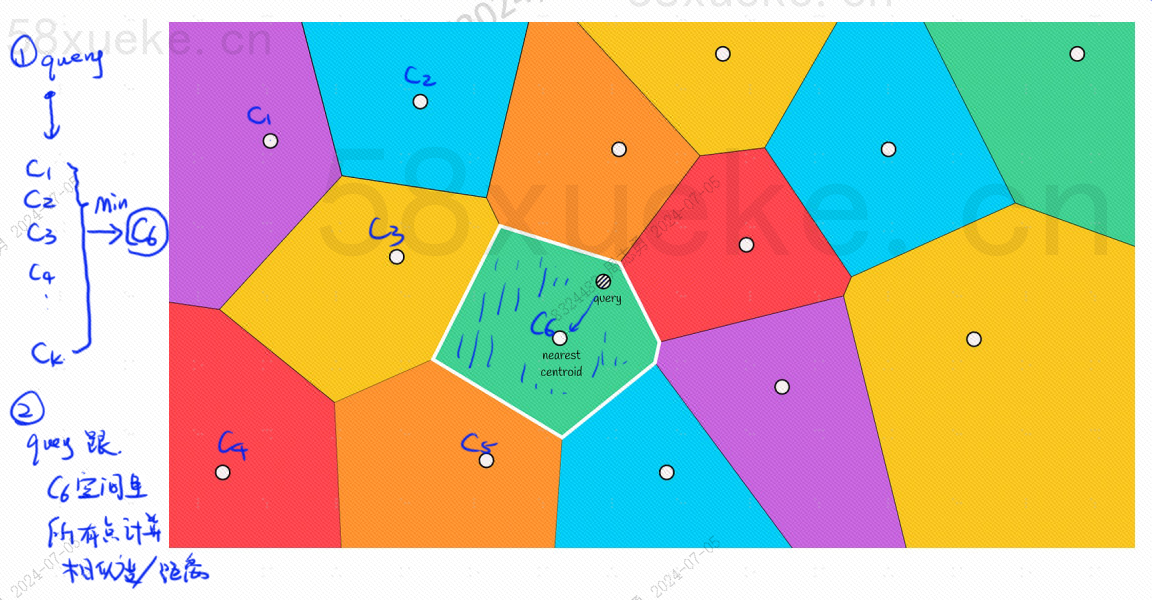
比如说上图中的查询步骤如下:
- 查询点距离最近的块为 C6(距离C6的中心点最近)
- 然后查询 C6 中距离最近,相似度最高的点
但是通过我们肉眼可以看出其中红色和橙色的块的中心点虽然离查询点远,但是它们块中的点离查询点近,这个时候就需要扩大搜索块的范围: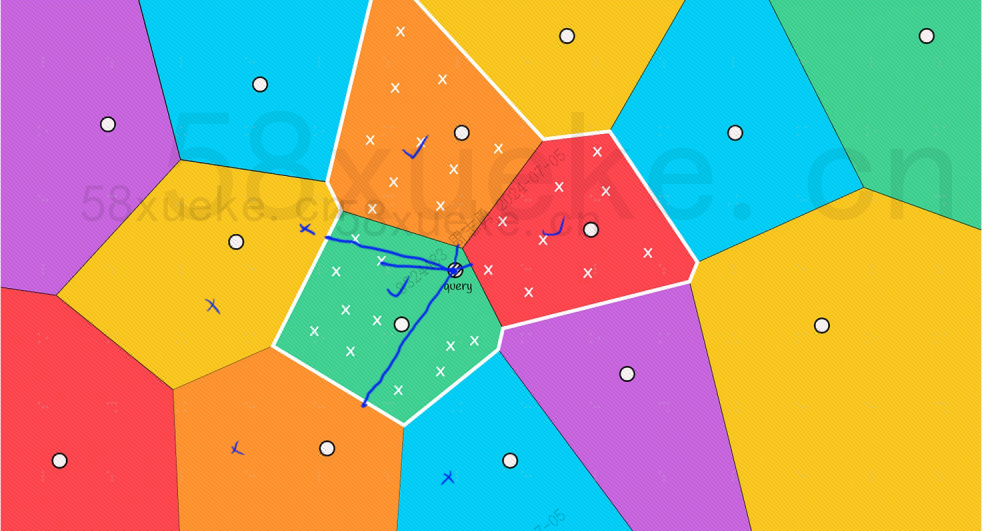
下边是求相似度最高和距离最近的算法公式,其中相似度最高(COS_SIM)是通过余弦计算,距离最近有两种算法,欧式算法和曼哈顿算法,这里就不展开讲解了:
Product Quantization(PQ)
PQ 算法首先会将所有向量划分为多个子空间,和近似 KNN 一样每个子空间都有一个中心点(centroid)。
然后会将原有高维向量拆分为多个低维向量子向量,使用距离该子向量最近的中心点作为该子向量的 PQ ID,然后一个高维向量就由多个 PQ ID 构成,大大压缩了空间。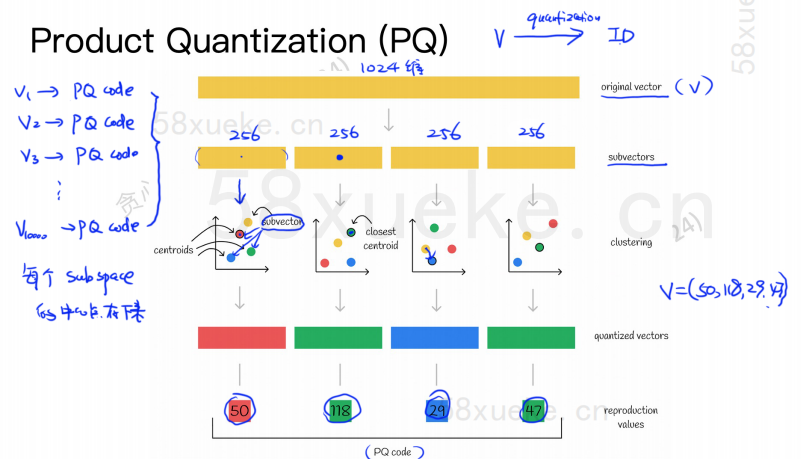
比如说上图中1024维的向量被拆分为4个 256维的子向量,然后这四个子向量距离最近的中心点分别为:50,118,29,47。因此,该1024 维的向量就可以用 V=(50,118,29,47) 表示,同时它的 PQ code 也是 (50,118,29,47) 。
因此使用 PQ 算法的向量数据库就需要保存所有中心点的信息以及所有高维向量的 PQ code。
假设现在我们有一个查询语句,需要从向量数据库中查询出相似度最高的向量,使用 PQ 算法该如何查询呢?
- 首先会将我们的查询语句转换为一个查询向量
- 然后该查询向量会和每一个向量的 PQ code 进行距离计算,其实也就是和 PQ code 中的每一个中心点进行距离计算然后相加,如下图所示:
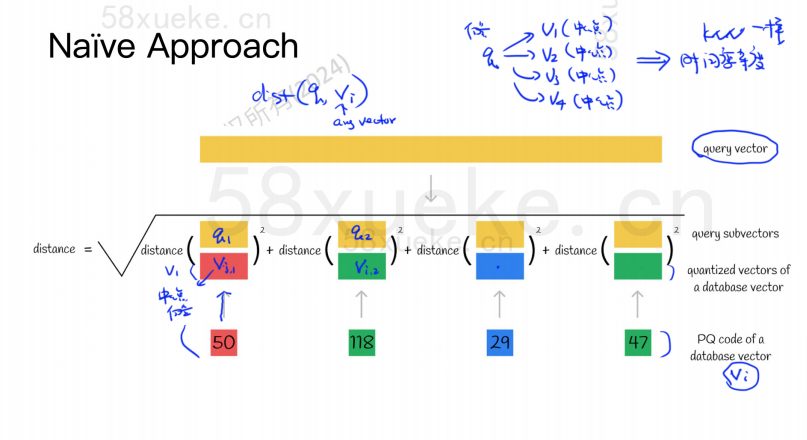
- 然后按照上边这种方式,和每一个子向量的 PQ code 进行计算,就可以算出距离最近的向量了,但是这种和中心点进行计算的算法会存在误差,如下图所示:
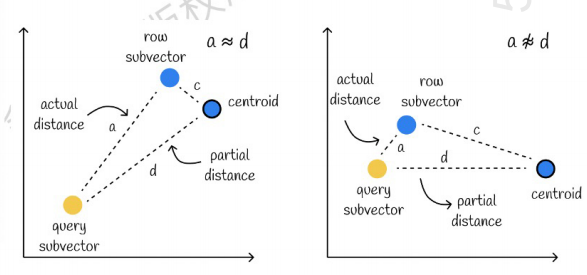
左边的是误差很小的情况,右边的是误差比较大的情况,一般会存在少数误差,但是大部分误差是比较小的。
使用缓存加速计算
如果说原始查询向量和每一个子向量的 PQ code 都需要进行一次距离计算,那么和近似 KNN 算法没有多大区别,空间复杂度都为O(n)*O(k),那么该算法的意义是什么呢?就只是单纯为了压缩,减少空间存储吗?
假设将所有向量划分为 K 个子空间,每一个子空间中有 n 个点,我们将每个子空间中的点到其中心点的距离提前计算出来,放到一个二维矩阵中,然后查询向量对应的每一个子向量到中心点的距离我们可以直接从矩阵中查询出来,如下图所示: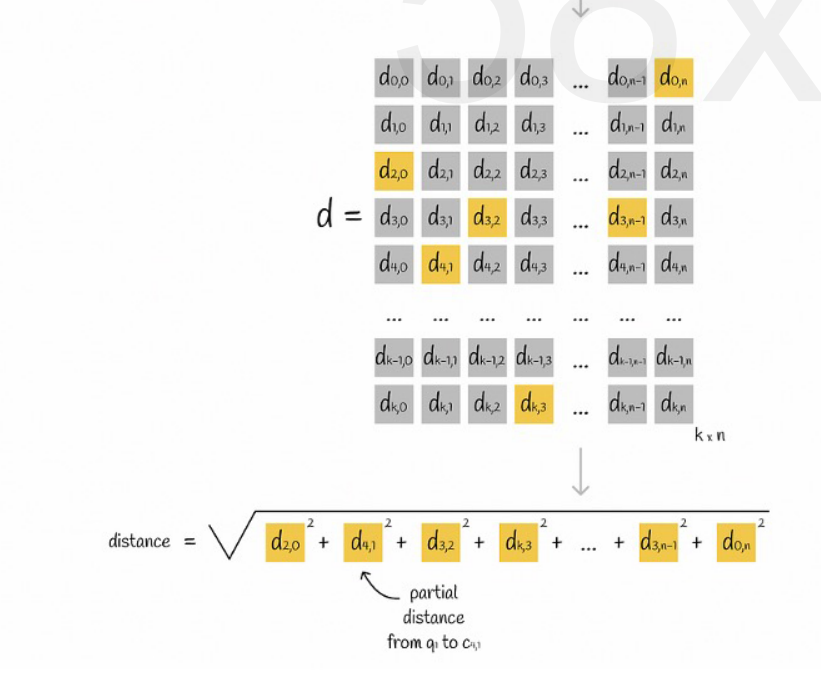
最后我们只需要将每个子向量的距离相加开平方根即可。
近似 KNN 与 PQ 算法结合
这两种算法是不冲突的,可以先使用近似 KNN,将所有向量划分为多个子空间,然后将查询向量定位到对应的子空间中。
这样再在子空间中使用 PQ 算法,加速计算。
NSW 算法搜索
在一个给定向量数据集中,按照某种度量方式,检索出与查询向量相近的K个向量(K-Nearest Neighbor,KNN),但由于KNN计算量过大,我们通常只关注近似近邻(Approximate Nearest Neighbor,ANN)问题。
NSW在构图时,每次随机选择点,加入图中。每次加入点都查找与其最近邻的m点以添加边。最终形成如下图所示的结构:
在搜索 NSW 图时,我们从预定义的入口点开始。这个入口点连接到附近的几个顶点。我们确定这些顶点中的哪一个最接近我们的查询向量并移动到那里。
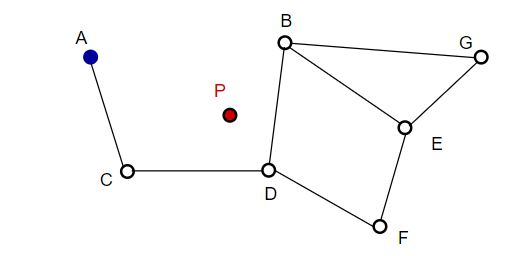
如从A开始,A的临近点C离P的距离更近更新。然后C的临近点D距离P更近,然后D的临近点B和F没有更近,程序停止,即为D点。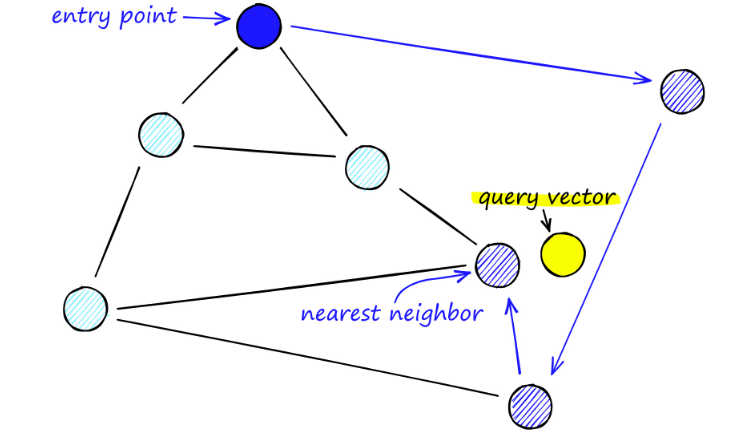
HNSW
图的构建从顶层开始。进入图表后,算法贪婪地遍历边,找到与我们插入的向量q最接近的ef邻居——此时ef = 1。
找到局部最小值后,它会向下移动到下一层(就像在搜索期间所做的那样)。重复这个过程,直到到达我们选择的插入层。这里开始第二阶段的建设。
ef值增加到我们设置的efConstruction参数,这意味着将返回更多最近的邻居。在第二阶段,这些最近的邻居是新插入元素q的链接的候选者, 并作为下一层的入口点。
经过多次迭代后,添加链接时还要考虑两个参数。M_max,它定义了一个顶点可以拥有的最大链接数,同样的M_max0,它定义了针对第 0 层中的顶点的最大连接数。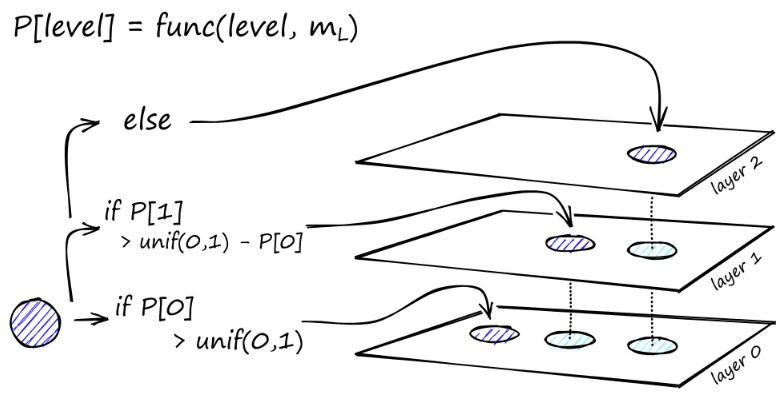
HNSW 代表 Hierarchical Navigable Small World,一个多层图。数据库中的每个对象都在最低层(图片中的第 0 层)中捕获。这些数据对象连接得很好。在最低层之上的每一层上,表示的数据点较少。这些数据点与较低层匹配,但每个较高层中的点呈指数级减少。如果有搜索查询,将在最高层找到最近的数据点。在下面的示例中,这只是多了一个数据点。然后它更深一层,从最高层中第一个找到的数据点中找到最近的数据点,并从那里搜索最近的邻居。在最深层,将找到最接近搜索查询的实际数据对象。
HNSW 是一种非常快速且内存高效的相似性搜索方法,因为只有最高层(顶层)保存在缓存中,而不是最低层中的所有数据点。只有最接近搜索查询的数据点在被更高层请求后才会被加载,这意味着只需要保留少量内存。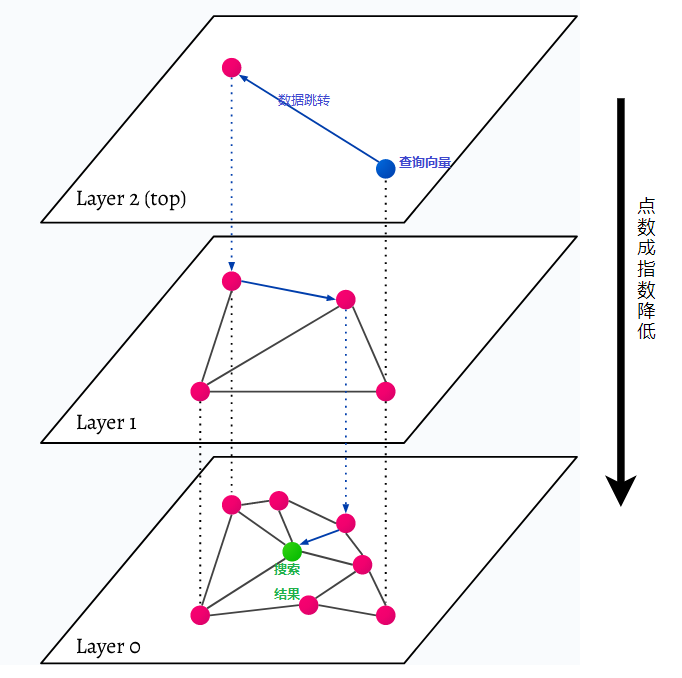












![[leetcode] largest-divisible-subset 最大整除子集](https://i-blog.csdnimg.cn/direct/87bb69dc74fb4c06a2cd982ddb6bcc0b.png)