一、知识概要

本节从正定矩阵的回顾谈起，介绍了相似矩阵和若尔当型。但是没有进行深入介绍，主要目的是让我们对这些变换方式有所了解。

二、正定矩阵补充

在上一节学习的正定矩阵的基础上，我们给出以下问题：
（1）正定矩阵的逆矩阵是否也是正定矩阵？
解：
·由于逆矩阵的特征值是原矩阵特征值的倒数，所以若 A 是正定矩阵，则𝑨−𝟏也是正定矩阵。
（2）假定 A 和 B 是正定矩阵，那么 A+B 呢？


对于正定矩阵，不需要进行“行交换”，也不必担心主元过小或者等于零。这可以简化我们的很多计算。

三、相似矩阵

对于两个 n 阶方阵 A 和 B，如果说两者相似，这意味着存在某个可逆矩阵 M，使得等式：

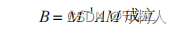
【例】设 A 具有无关的特征向量，则由前面几节的知识知道：


结论：相似矩阵特征值相同（事实上，其线性无关的特征向量数目也一样）

四、若尔当型

4.1 重特征值的相似情况

结论：对于之前不能完成相似对角化的矩阵，都可以通过某种特殊方法，完成近似的“对角化”。如若尔当标准型。

4.2 若尔当型
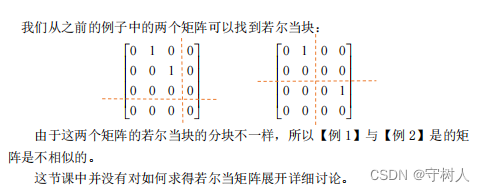
由上面我 4.1 可知，若尔当型出现的背景是特征值数量相同，但是矩阵不相似情况。接下来我们来举两个个具有四重根的例子

五、学习感悟

本节对相似矩阵，若尔当块进行了介绍，主要从正反两方面了解了矩阵相似时对应特征值情况。进而引出了若尔当阵的判断方法。但是并没有对它的求解过程进行深入了解。