摘要：

方向梯度直方图(HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述。HOG特征通过计算和统计图像局部区域的梯度方向直方图来构成特征。主要用于解决人体目标检测，主要通过梯度方向直方图特征来表达人体，提取人体的外形信息和运动信息，形成丰富的特征集。

一：HOG特征

1.主要思想
在一副图像中，局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。其本质为：梯度的统计信息，而梯度主要存在于边缘的地方。Hog特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。
2.实现方法
首先将图像分成小的连通区域，这些连通区域被叫做细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来，就可以构成特征描述符。
3.性能提高
将这些局部直方图在图像的更大的范围内（叫做区间）进行对比度归一化，可以提高该算法的性能，所采用的方法是：先计算各直方图在这个区间中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后，能对光照变化和阴影获得更好的效果。

二：实现步骤

1、色彩和伽马归一化
为了减少光照因素的影响，首先需要将整个图像进行规范化（归一化）。在图像的纹理强度中，局部的表层曝光贡献的比重较大，所以，这种压缩处理能够有效地降低图像局部的阴影和光照变化。通常用的方法为标准化gamma空间：$I(x,y)=I(x,y{)}^{\frac{1}{2}}$，其中 I(x,y) 为像素值。
2、计算图像梯度
计算图像横坐标和纵坐标方向的梯度，并据此计算每个像素位置的梯度方向值；求导操作不仅能够捕获轮廓，人影和一些纹理信息，还能进一步弱化光照的影响。
水平方向梯度 $G_x(x,y)=I(x+1,y)-I(x-1,y)$
垂直方向梯度 $G_{\mathrm{y}}(x,y)=I(x,y+1)-I(x,y-1)$
梯度幅值 $G(x,y) = \sqrt {G_X^2 + G_y^2} $
梯度方向 $\alpha (x,y)=\arctan \frac{G_x}{G_y}$
3、构建方向的直方图
细胞单元中的每一个像素点都为某个基于方向的直方图通道投票。投票是采取加权投票的方式，即每一票都是带有权值的，这个权值是根据该像素点的梯度幅度计算出来。可以采用幅值本身或者它的函数来表示这个权值，实际测试表明： 使用幅值来表示权值能获得最佳的效果，当然，也可以选择幅值的函数来表示，比如幅值的平方根、幅值的平方、幅值的截断形式等。细胞单元可以是矩形的，也可以是星形的。直方图通道是平均分布在0-1800（无向）或0-3600（有向）范围内。
4、将细胞单元组合成大的区间
由于局部光照的变化以及前景-背景对比度的变化，使得梯度强度的变化范围非常大。这就需要对梯度强度做归一化。归一化能够进一步地对光照、阴影和边缘进行压缩。
采取的办法是： 把各个细胞单元组合成大的、空间上连通的区间。这样，HOG描述符就变成了由各区间所有细胞单元的直方图成分所组成的一个向量。这些区间是互有重叠的，这就意味着：每一个细胞单元的输出都多次作用于最终的描述器。
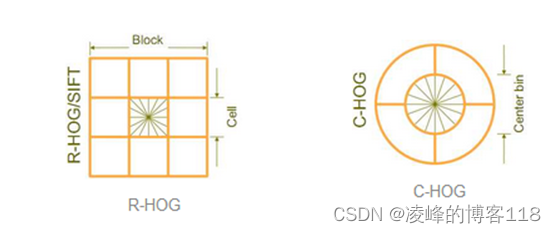
区间有两个主要的几何形状——矩形区间（R-HOG）和环形区间（C-HOG）。R-HOG区间大体上是一些方形的格子，它可以有三个参数来表征：每个区间中细胞单元的数目、每个细胞单元中像素点的数目、每个细胞的直方图通道数目。
5、收集HOG特征
把提取的HOG特征输入到SVM分类器中，寻找一个最优超平面作为决策函数。

三：HOG的优点

1.由于HOG是 在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。
2.在粗的空域抽样、精细 的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响 检测效果。

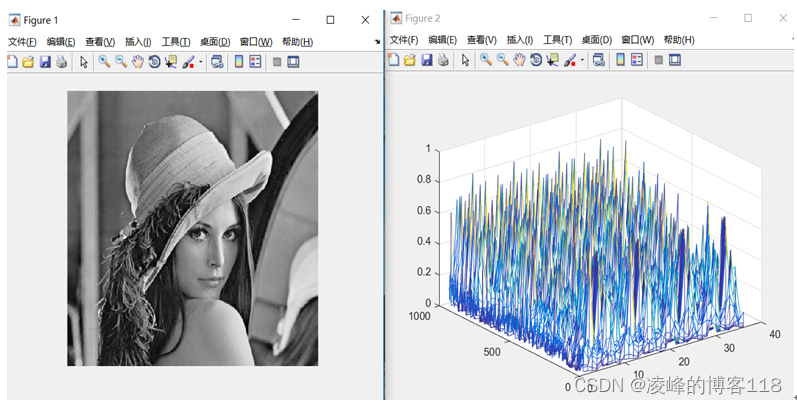
四、仿真结果：

下图是lenna 512*512大小的灰度图像得到的HOG直方图。