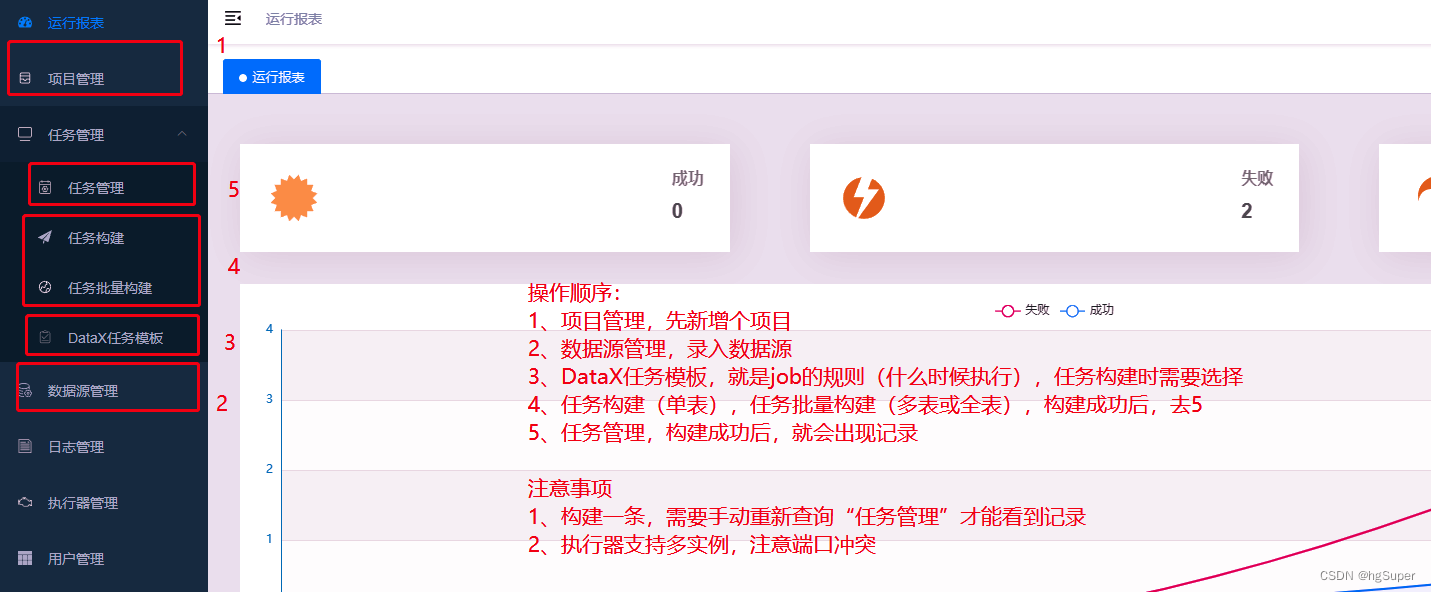
文章目录
- 前言
- 一、简单选择排序
- 1.简介
- 2.算法思路
- 3.代码实现
- 二、堆排序
- 1.简介
- 2.算法思路
- 3.代码实现
- 总结
前言
堆排序是选择排序的一种,今天我们讲解一下堆排序和简单选择排序
一、简单选择排序
1.简介
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
时间复杂度:O(n²) 稳定性:不稳定
2.算法思路
动态显示图,充分理解选择排序

从图中我们可以看见:
- 第一趟在未排序序列寻找最小值,然后放在序列的起始位置
- 第二趟,从已排好的元素后面开始寻找最小值,然后再放在最前端
- 依次寻找,排序…直到所有元素依次排好。
3.代码实现
简单选择排序:
void select_sort(int *p,int n)\n
{
int i,j;
int min = 0;
for(i = 0;i < n - 1;i++)//排序次数
{
min = i;
for(j = i + 1;j < n;j++)
{
if(p[j] < p[min])
{
min = j;//记录交换的元素下标值
}
}
if(i != min)
{
int temp = p[i];
p[i] = p[min];
p[min] = temp;
}
int main()
{
int arr[num] = { 3,1,4,5,2,7,9,0,8,6 };
select_sort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
}
那思考一下,能否进行改进呢?比如,我们同时找最大值最小值,然后将最小值放序列前端,最大值放序列末端。
代码实现:
void swap(int* q, int* a)
{
int tem = *q;
*q = *a;
*a = tem;
}
void select_sort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int min = begin, max = begin;
for (int i = min; i < end; i++)
{
if (a[i] < a[min])
min = i;
if (a[i] > a[max])
max = i;
}
swap(&a[min], &a[begin]);
// begin == maxi时,最大被换走了,修正一下maxi的位置
if (begin == max)
max = min;
swap(&a[max], &a[end]);
begin++; end--;
}
}
int main()
{
int arr[num] = { 3,1,4,5,2,7,9,0,8,6 };
select_sort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
}
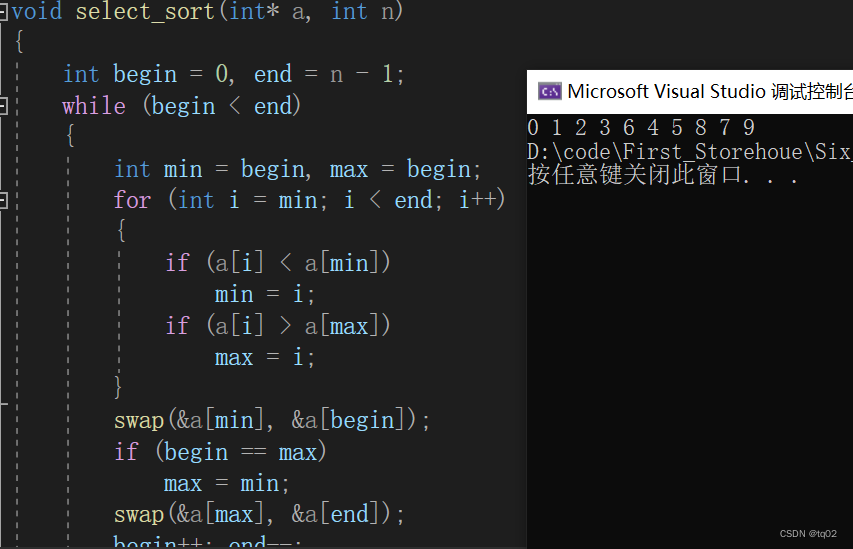
在使用这个代码时,得小心当begin位置处于max的下标,min和begin互换之后,max在的下标值则是已经更换,最大值在min的下标值了,所以需要进行判断。
运行结果:
二、堆排序
1.简介
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
时间复杂度:O(N*logN) 空间复杂度:O(1) 稳定性:不稳定
而如果想使用堆排序,则需要先建立堆,然后选择大推或者小堆排序
2.算法思路
- 将初始待排序关键字序列(R0,R1,R2…Rn)构建成大顶堆,此堆为初始的无序区。
- 将堆顶元素R[0]与最后一个元素R[n]交换,此时得到新的无序区(R0,R1,R2,…Rn-1)和新的有序区(Rn)。
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R0,R1,R2,…Rn-1)调整为新堆,然后 再次将R[1]与无序区最后一个元素交换,得到新的无序区(R0,R1,R2…Rn-2)和新的有序区(Rn-1,Rn)。
- 不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成
堆图像展示和讲解:
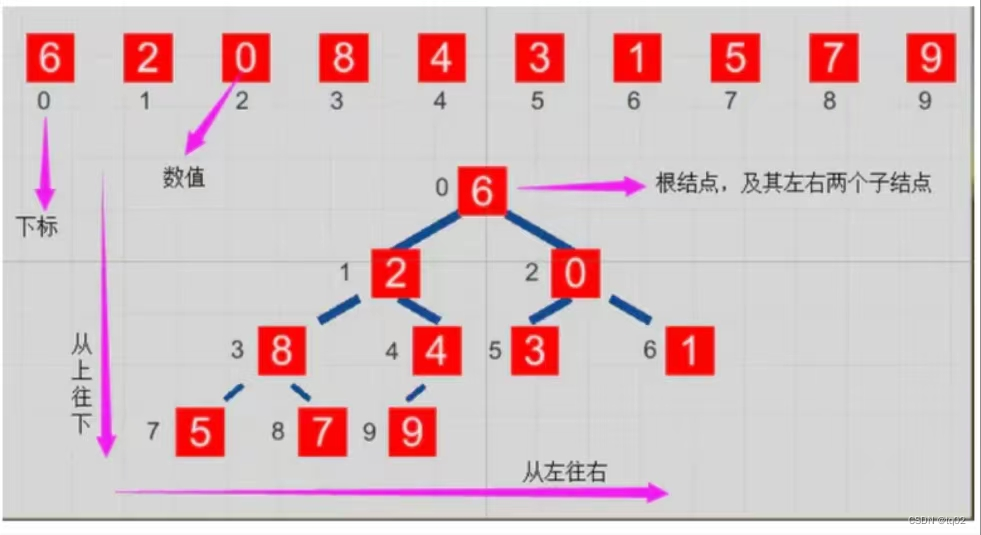
大堆构建的动态显示图:

耐心观看,我们可以看见,先变成了大堆顶(堆顶元素最大,父亲节点大于孩子节点),然后堆顶元素和最后一个元素交换,最后一个元素变成堆顶元素,然后和最大的孩子结点进行交换,最后将第二大的叶子结点交换上来,变成堆顶元素,而原来的元素则需要调整到适合它的位置。
红色是已排序的有序区间 黄色是调换堆顶元素和末尾元素 绿色是待排序区间
注:重点在于建堆(大堆和小堆)
3.代码实现
代码如下:
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中小的那一个
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
// 如果小的孩子小于父亲,则交换,并继续向下调整
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// 堆排序
void HeapSort(int* a, int n)
{
// O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
int main()
{
int arr[num] = { 3,1,4,5,2,7,9,0,8,6 };
HeapSort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
}
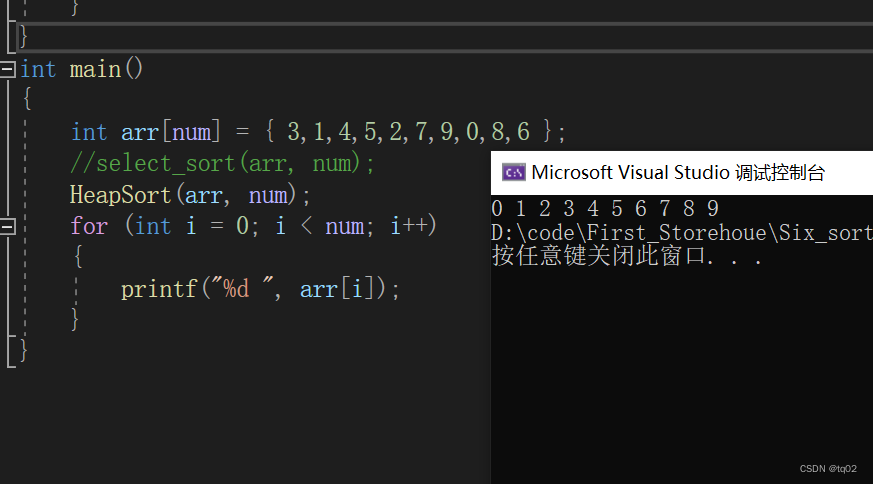
运行结果:
总结
堆排序比较难以理解,可以通过画图来消化,并且重点在于建堆。
文章的动态图全是小小作者我在网上寻找到的,认为最为合适并且容易理解的图。本文的图全部来源于百度
本人认为堆排序比较难以理解,千位要画图理解,各位努力学习的IT人员们,一起加油努力哦。祝各位学业有成,财源滚滚。
---------来自菜鸟TQ02的祝福语