训练误差和泛化误差

训练误差（training error）是指，模型在训练数据集上计算得到的误差。泛化误差（generalization error）是指，模型在新数据上的误差。

K-折交叉验证

当训练数据稀缺时，我们甚至可能无法提供足够的数据来构成一个合适的验证集。这里我们采用K-折交叉验证的方法：将训练数据分割成K块，使用第i（0<i<=k）块作为验证数据集，其余的作为验证数据集，最后，通过对K次实验的结果取平均来估计训练和验证误差。

欠拟合和过拟合

过拟合是指模型能很好地拟合训练样本，但对新数据的预测准确性很差。
欠拟合是指模型不能很好地拟合训练样本，且对新数据的预测准确性也不好。
是否过拟合或欠拟合可能取决于模型复杂性和可用训练数据集的大小。

模型复杂性

高阶多项式函数比低阶多项式函数复杂得多。高阶多项式的参数较多，模型函数的选择范围较广。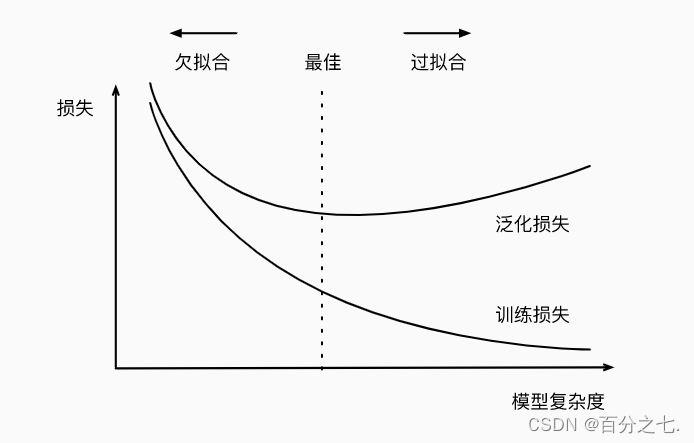在这里插入图片描述

数据集大小

训练数据集中的样本越少，我们就越有可能（且更严重地）过拟合。随着训练数据量的增加，泛化误差通常会减小。对于固定的任务和数据分布，模型复杂性和数据集大小之间通常存在关系。给出更多的数据，我们可能会尝试拟合一个更复杂的模型。能够拟合更复杂的模型可能是有益的。如果没有足够的数据，简单的模型可能更有用。对于许多任务，深度学习只有在有数千个训练样本时才优于线性模型。从一定程度上来说，深度学习目前的生机要归功于廉价存储、互联设备以及数字化经济带来的海量数据集。

权重衰减

我们总是可以通过去收集更多的训练数据来缓解过拟合。但这可能成本很高，耗时颇多，或者完全超出我们的控制，因而在短期内不可能做到。假设我们已经拥有尽可能多的高质量数据，我们便可以将重点放在正则化技术上。权重衰减（weight decay）是最广泛使用的正则化的技术之一，它通常也被称为L2正则化。
在这里插入图片描述
每一次权重更新，也就是每一次梯度下降法的学习，w的权重都要进行一些缩小，也叫做w的系数衰减。
使用L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。在实践中，这可能使它们对单个变量中的观测误差更为稳定。相比之下，L1惩罚会导致模型将权重集中在一小部分特征上，而将其他权重清除为零。

权重衰减简洁实现

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none')
    num_epochs, lr = 100, 0.003
    trainer = torch.optim.SGD([
        {"params":net[0].weight,'weight_decay': wd},#实例化优化器时直接通过weight_decay指定weight decay超参数
        {"params":net[0].bias}], lr=lr)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())
    train_concise(0)
    #w的L2范数： 14.670721054077148
    train_concise(3)
    #w的L2范数： 0.3454631567001343

wd=0:
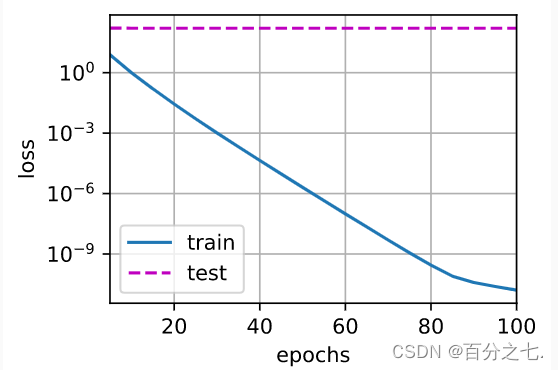
在这里插入图片描述
wd=3:

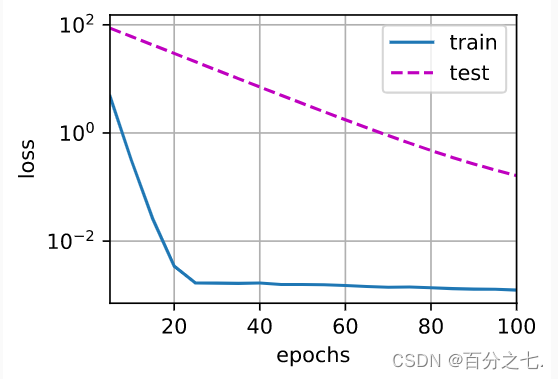
正则化是处理过拟合的常用方法：在训练集的损失函数中加入惩罚项，以降低学习到的模型的复杂度。

暂退法（Dropout）

暂退法在前向传播过程中，计算每一内部层的同时注入噪声，这已经成为训练神经网络的常用技术。这种方法之所以被称为暂退法，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些节点置零。
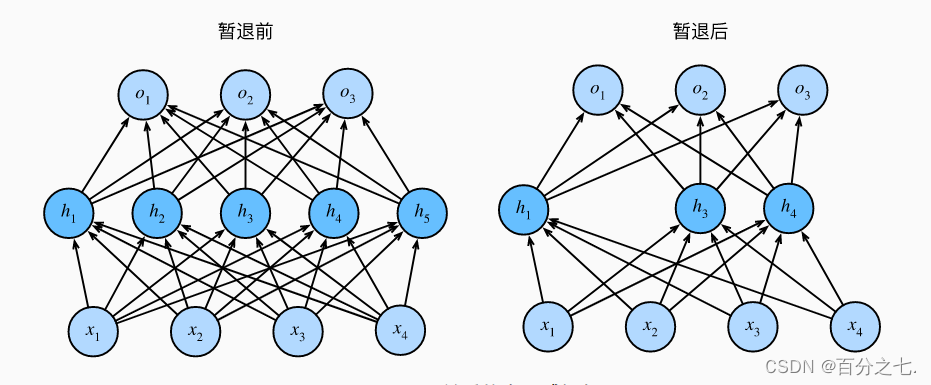
在这里插入图片描述
图中删除了h2和h5，因此输出的计算不再依赖于h2或h5，并且它们各自的梯度在执行反向传播时也会消失。这样，输出层的计算不能过度依赖于h1,…h5的任何一个元素。通常，我们在测试时不用暂退法。给定一个训练好的模型和一个新的样本，我们不会丢弃任何节点，因此不需要标准化。
在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。换言之，每个中间活性值h以暂退概率p由随机变量h′替换，如下所示：
$h^{\prime}= \begin{cases}0 & \text { 概率为 } p \\ \frac{h}{1-p} & \text { 其他情况 }\end{cases}$
根据此模型的设计，其期望值保持不变，即E[h′]=h。

丢弃法将一些输出项随机置0来控制模型复杂度
常作用在多层感知机的隐藏层输出上
丢弃概率在控制模型复杂度的超参数中设置（0<p<1）

从零开始实现Dropout

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

简洁实现

我们只需在每个全连接层之后添加一个Dropout层，将暂退概率作为唯一的参数传递给它的构造函数。在训练时，Dropout层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。在测试时，Dropout层仅传递数据。

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);