47 转置卷积【动手学深度学习v2】】

深度学习学习笔记
学习视频：https://www.bilibili.com/video/BV17o4y1X7Jn/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=75dce036dc8244310435eaf03de4e330

转置卷积

卷积不会增大输入的高宽，无法通过padding很好的将高宽增加，卷积不断将图片减小的话，语义分割没法很好的把像素级别输出，于是用到转置卷积，能够很好的把输入高宽增大。

操作：每个数 会跟卷积核中每个元素做乘法，得到多个矩阵，然后将这些矩阵加起来。

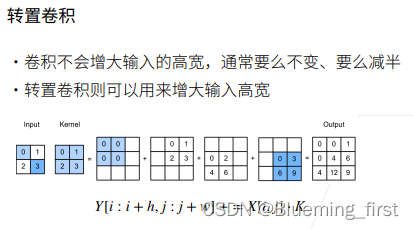
为什么称为“转置”：卷积可以等价于矩阵乘法，转置卷积等价于 转置矩阵再相乘。
如果使用卷积将 4 * 4 变成 2 * 2 的话，你可以使用转置卷积将 2 * 2 变回 4 * 4。

QA：

1. 转置卷积实现将图片放大。
2. 转置卷积就是反卷积。
3. 转置卷积可以实现线性插值，但是转置卷积不仅仅做线性插值。
4. 语义分割要的是标号，不是一直在变的，卷积不断的sum，通道中存入不同的空间信息，虽然高宽变小但是它做了总结，feature map虽然变小了，但是它的信息并没有丢失。
5. 不断变大：要对每个像素做预测。
6. 转置卷积不是还原，只是形状发生变化，不是还原值。
7. 转置卷积不算是上采样，只是为了得到像素的输出。
8. 卷积+转置卷积有些encoder和decoder的感觉。

47.2 转置卷积是一种卷积

转置卷积是一种卷积，对输入和核做了重新的排列，卷积一般做下采样，转置卷积做上采样。使用同样超参数的卷积核上转置卷积核、卷积是逆变换。

如何将转置卷积换算为卷积：
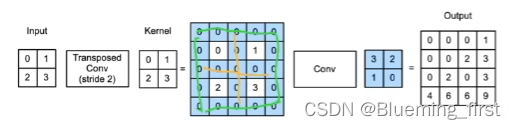
列子：输入 2 * 2 核 2 * 2 ，对输入上下左右填充 k -1 （蓝色区域），核做上下左右翻转，然后做正常的卷积，得到 3 * 3 输出 就等价于 转置卷积的输出。

填充为 p ：输入填充 k - p - 1（k 是核窗口），核矩阵同样做上下左右的翻转，然后做卷积（填充为0 ，步幅为1）。
假设填充为p 步幅为1 ：在行和列之间插入 s - 1（蓝色部分），再填充 边上，然后卷积得到 4 * 4 输出。

形状换算：
卷积是 + 2p这里有错误

转置卷积

import torch
from torch import nn
from d2l import torch as d2l

实现基本的转置卷积运算

# 实现转置卷积的公式 K : kernel（卷积核）
def trans_conv(X, K):
    h, w = K.shape
    # X.shape[0] + h - 1 转置卷积之后的形状（卷积是X.shape[0]-h+1）
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            # 计算
            Y[i:i + h, j:j + w] += X[i, j] * K
    return Y

验证上述实现输出

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)

tensor([[ 0.,  0.,  1.],
        [ 0.,  4.,  6.],
        [ 4., 12.,  9.]])

使用高级API获得相同的结果

# 1 批量大小 1 通道数
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
# ConvTranspose2d 转置卷积  1, 1 输入输出通道数 bias=False 不需要偏差
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[ 0.,  0.,  1.],
          [ 0.,  4.,  6.],
          [ 4., 12.,  9.]]]], grad_fn=<SlowConvTranspose2DBackward>)

填充、步幅和多通道

# 这里 padding 输出减小了
# 用填充到输出的最外面一圈，这样输出从 3 * 3 变成 1* 1
# 计算公式与卷积相反：x + w - 1 - padding = 2 + 2 -1 -2 = 1
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[4.]]]], grad_fn=<SlowConvTranspose2DBackward>)

# stride=2 增大stride会把输出变大，2 * 2 变成 4 * 4
# 卷积是除以stride， 转置卷积是 乘以 stride
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[0., 0., 0., 1.],
          [0., 0., 2., 3.],
          [0., 2., 0., 3.],
          [4., 6., 6., 9.]]]], grad_fn=<SlowConvTranspose2DBackward>)

# 多通道没有变化
X = torch.rand(size=(1, 10, 16, 16))

conv = nn.Conv2d(
    10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(
    20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

True

与矩阵变换的联系

X = torch.arange(9.0).reshape(3, 3) # 3 * 3
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]]) * 2 * 2 kernel
Y = d2l.corr2d(X, K) # 卷积
Y

tensor([[27., 37.],
        [57., 67.]])

# 变成 V 矩阵 构造 4 * 9 的矩阵
def kernel2matrix(K):
    k, W = torch.zeros(5), torch.zeros((4, 9))
    k[:2], k[3:5] = K[0, :], K[1, :]
    W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, k
    return W

W = kernel2matrix(K)
W

tensor([[1., 2., 0., 3., 4., 0., 0., 0., 0.],
        [0., 1., 2., 0., 3., 4., 0., 0., 0.],
        [0., 0., 0., 1., 2., 0., 3., 4., 0.],
        [0., 0., 0., 0., 1., 2., 0., 3., 4.]])

# reshape成一个向量
Y == torch.matmul(W, X.reshape(-1)).reshape(2, 2)

tensor([[True, True],
        [True, True]])

# Y 对 K 做转置卷积 等价于 W.T reshape为3 * 3
Z = trans_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)

tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])