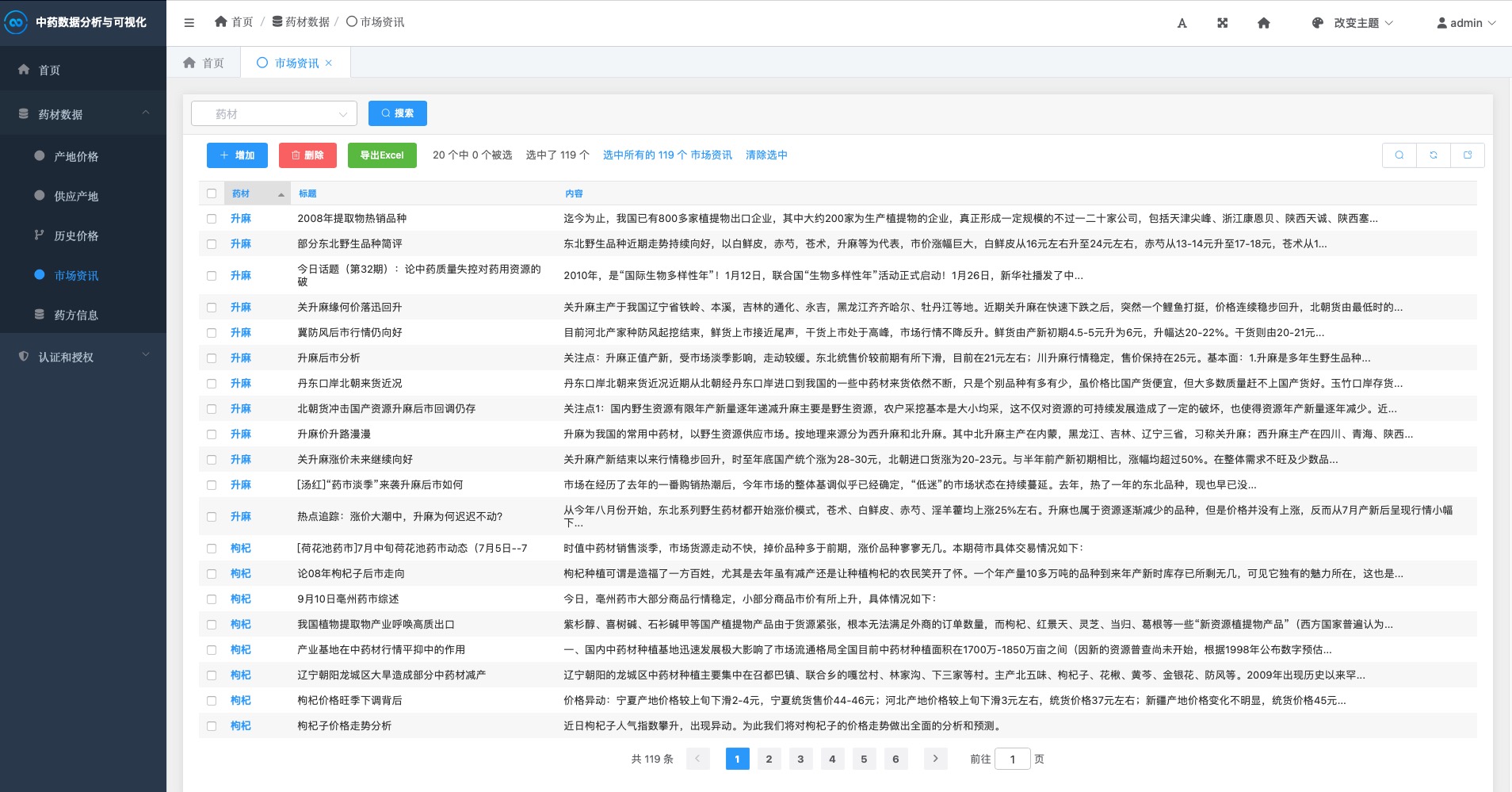
多变量系统知识回顾 - MIMO system

这一章对深入理解多变量系统以及鲁棒分析至关重要

首先，对于如下系统：

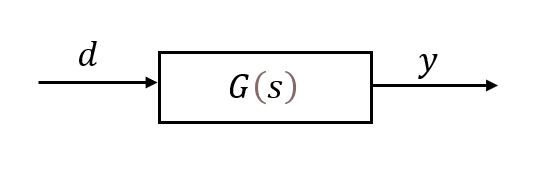
当G(s)为单输入，单输出系统时：

如果：

则：

所以

因此，对于SISO，系统的增益跟w有关系，

当G(s)为MIMO时，例如2X2时，

假设输入信号为：

 

输出信号为：

则：

对于MIMO，系统的输入和输出均为矢量矩阵,所以系统的增益为：

因此对于MIMO，根据上式可知，系统的增益跟输入信号的方向有关系。

下面用具体的实例来进一步说明。

例如：

根据：

可知：

其中，在系统的响应中 

为G的最大singular value，为G的最小singular value

用MATLAB求取矩阵的singular value的代码如下：

clear all;clc;
G1=[5 4; 3 2];
[U S V]=svd(G1)

程序运行结果如下：

U =

   -0.8718   -0.4899
   -0.4899    0.8718


S =

    7.3434         0
         0    0.2724


V =

   -0.7937    0.6083
   -0.6083   -0.7937

所以：

如果取横坐标为：,纵坐标为：,我们可以得到如下图示结果：

如果G是一个传递函数呢？

例如：，我们可以利用MATLAB得到在一定频率范围内，系统的最大相应。

MATLAB 代码如下：

clear all;clc;
s=tf('s');
G=[1/(s^2+2*s+100) 1/(s+50); 1/s+10 1/(s+300)];
sigma(G)
grid on

程序运行结果如下：

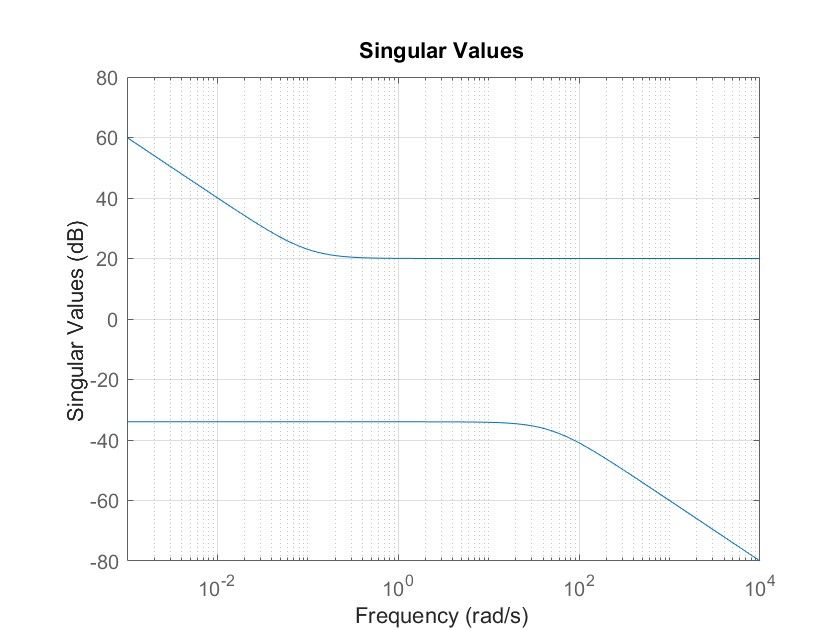
根据上述结果，我们可以知道在频率大于1rad/s时，系统的最大响应为20dB。

接下来我们将引入鲁棒分析的设计概念。

最后，欢迎大家有问题给我留言。

非常感谢小伙伴们的-点赞-收藏-加关注。