目录
0. 前言
2. 量子多重H门
3. 量子SWAP门
4. 量子CNOT门(CX门):受控非门
5. 量子CY和CZ门
6. 量子C*门
6.1 受控S门
6.2 受控H门
6.3 受控Z旋转门
6.4 受控X旋转门
6.4 受控Y旋转门
7. 量子托佛利门(CCNOT门)
8. 量子弗雷德金门(CSWAP门)
0. 前言
量子计算、量子信息、量子编程自学笔记系列。
用自己能看懂的方式来表述对于量子计算基础知识的理解。
不求体系完备和逻辑严谨、但求通俗易懂。或能顺便给路过的小伙伴一些参考和启发那是纯属巧合概不认账^-^。当然,仅限于轮廓的勾勒和要点简述,对细节感兴趣的话还是要亲自正儿八经地啃正经的参考书。
本节介绍用于多个量子比特的操作的量子门。单个量子比特的操作无法使量子比特之间发生“化学反应”--纠缠。虽然对单量子比特的门操作也是不可或缺的,但是只有多比特量子门作用于多个量子比特才能真正的产生有趣的事情。
回顾一下,当我们有n个量子比特构成一个量子系统Q时,Q的状态空间为维度为维,可以用一个
维复希尔伯特空间来表示量子系统Q的状态空间。可以将其简记为
,这个符号的意思表示它是由n个复希尔伯特空间
的张量积构成的张量积空间。
量子系统Q的基向量可以简记为,又可以进一步用一个十进制无符号数来表示,但是此时需要标记清楚量子数n,比如说在n=8时,以下两种标记法是等价的:
2. 量子多重H门
量子门(但是标题上不允许出现这种符号,故杜撰了名字“多重H门”,勿要当真^-^)。
前面已经介绍过H门的矩阵为:,简单计算可以得到H门作用于计算基底向量的效果如下:
它将两个基向量变换成了两个等概率叠加态。H门在量子电路中的作用就是用于创建叠加态,它通常用在量子电路的最前端。
将H矩阵同时作用于两个量子比特时是什么效果呢?考虑两个量子比特状态(注意,以下用下标来表示各计算基是属于哪个量子比特的)
,
将H矩阵作用于量子比特相当于:
其中, ,这是一个4x4的幺正矩阵。
虽然以上公式写得这么花里胡哨,其实,所用于量子比特得效果就是用两个量子H门分别作用于其中一个量子比特。通常用于将两个初始化均为
得量子比特调整至叠加态。
依此同理类推,写成
的幺正矩阵主要是为了方便数学推导处理吧。
需要注意的一点是可以以递推的方式生成,如下所示:
3. 量子SWAP门
前面介绍张量积的时候说过张量积是不可交换的,即,通常来说:
量子SWAP门,字面意思就是交换门。问题是交换什么呢?交换以上张量积的顺序!
令M表示量子SWAP门的矩阵,则有:
令:,
,则上式可以展开为:
需要注意的是,等式左边是第一个量子比特在前第二个量子比特在后的表示(用下标(12)表示),而等式右边是第二个量子比特在前第一个量子比特在后的表示(用下标(21)表示)。
但是,从测量的角度来说,与
是无法区分的,其它四种双量子基态同理。因此,以上式子中的表示两个量子比特顺序的下标可以去掉。进一步改用坐标形式的表示的话就可以得到:
由此可以看出,M实际上就是一个4x4的置换矩阵:
4. 量子CNOT门(CX门):受控非门
CNOT门,用于创建纠缠的量子比特,是量子计算中最重要的门之一。C指Controlled,受控的,NOT门即量子非门、也即量子X门,连起来就是执行有条件地进行量子比特翻转的门,也称CX门。
CNOT门有两个量子比特输入,两个量子比特输出(这是因为量子门必须是可逆的,因此输出和输入的个数必须相等)。记两个量子比特分别为和
,它们的量子态分别为
和
。CNOT门的工作方式是:
如果为
,则
的状态由
变为
;
如果为
, 则
的状态保持不变;
的状态始终保持不变;
CNOT门的矩阵也是一个置换矩阵: ,左上角为2x2的单位矩阵(ID门,对应于第一个量子比特不发生变化),右下角是单量子X门的矩阵。
CNOT门作用于的标准基底的效果如下:
根据线性性质可得:
在CNOT门前、后各使用一个能够改变基底的H门可以得到一个有趣的结果,如下所示:
它实现了 的标准右矢表达式中第二项和第四项系数的置换操作。更具体一点来说,它的等价效果是,当第二个量子比特为
时,则翻转第一个量子比特;否则保持不变。也就是说它仍然实现了受控非门的功能,但是控制比特由CX的第一个量子比特变成了第一个量子比特!与CNOT门的行为刚好相反,所以有时也被称为逆CNOT门(reverse CNOT)。
CNOT门可用于构建贝尔纠缠态,具体构建方式后面再讨论。CNOT门符号图如下所示:
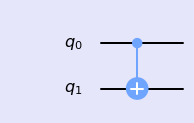
5. 量子CY和CZ门
与CX(受控X门)一样,以量子Y门、量子Z门为基础可以创建对应的受控Y门(CY门)和受控Z门(CZ门)。
(参考CX门的矩阵的构建方式)CY门的矩阵如下所示,左上角为2x2的单位矩阵(ID门,对应于第一个量子比特不发生变化),右下角是单量子Y门的矩阵。
同样可得CZ门的矩阵如下所示, 左上角为2x2的单位矩阵(ID门,对应于第一个量子比特不发生变化),右下角是单量子Z门的矩阵。
6. 量子C*门
参考前两节的受控X门、受控Y门和受控Z门的矩阵的构建方式,容易猜到通用的受控某某门的构建方式。
一般来说,如果是一个幺正矩阵,则我们已经知道它代表量子门(可以称为量子U门)的矩阵。那么受控U门的矩阵就是:
所以,我们得到了一族量子门!
6.1 受控S门
S门 --> 受控S门
6.2 受控H门
6.3 受控Z旋转门
6.4 受控X旋转门
6.4 受控Y旋转门
7. 量子托佛利门(CCNOT门)
托佛利门(Toffoli gate)是作用于3个量子比特的双控制式量子门,也称CCNOT门,或者CCX门。如果前两个量子比特的状态均为,则第三个量子比特翻转(即用X门作用于对第三个量子比特),否则,第三个量子比特保持不变。前两个量子比特总是保持不变。
托佛利门的矩阵为8x8置换矩阵,如下所示:
如以上矩阵所示,托佛利门的效果是交换最后两个系数。
托佛利门符号图如下所示:
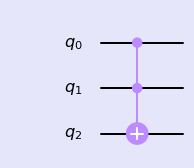
8. 量子弗雷德金门(CSWAP门)
弗雷德金门(Fredkin gate)也称CSWAP门,是作用于操作3个量子比特的单控制式量子门(与之相对的是,托佛利门是双控制式3量子比特门)。
如果第一个量子比特的状态是,则用SWAP门作用于第二个和第三个量子比特;否则,保持全部不变。第一个量子比特总是保持
弗雷德金门的矩阵为8x8置换矩阵,如下所示:
如以上矩阵所示,弗雷德金门的效果是交换倒数第二个和倒数第三个系数。弗雷德金门的符号图如下所示:
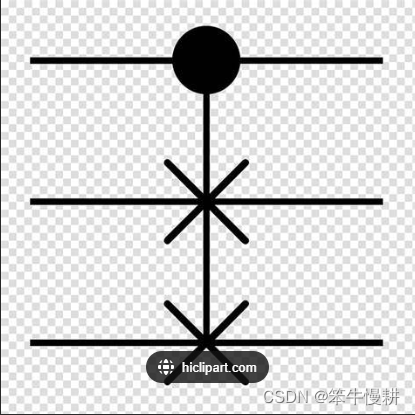
小结:
至此,本文和(量子笔记:单比特量子门、泡利矩阵)一起已经完成了一整套量子门的介绍,接下来可以用这些量子门来尝试着搭建量子电路了。。。coming soon!
参考文献
[1] 人人可懂的量子计算,克里斯.伯恩哈特著,邱道文等译,机械工业出版社
[2] 量子计算:一种应用方法,杰克.希德里著,姚彭晖等译,人民邮电出版社
[3] 与量子比特共舞,罗伯特.S.苏托尔著,吴攀译,人民邮电出版社
[4] 图解量子计算机,宇津木健著,胡屹译,人民邮电出版社
[5] Introductory Quantaum Computing (q4quanta.github.io)