一.栈模拟


二.单调栈求最大矩形面积

通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数 n 开始,表示组成直方图的矩形数目。
然后跟随 n 个整数 h1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为 1。
同行数字用空格隔开。
当输入用例为 n=0 时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
1≤n≤100000
0≤hi≤1000000000
输入样例:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例:
8
4000
思考:这个题为什么可以用单调栈呢:
例如:栈中有1,4,6而这时来了一个3,你会发现有1和将要插入的3的时候这个4,6是用不着的,这是4和6就可以出栈,这不就是一个单调递增的栈吗?
代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
//l[i], r[i]表示第i个矩形的高度可向两侧扩展的左右边界
int h[N], q[N], l[N], r[N];
typedef long long ll;
int main()
{
int n;
while(scanf("%d", &n), n)
{
for(int i = 1; i <= n; i ++) scanf("%d", &h[i]);
h[0] = h[n + 1] = -1;
int tt = -1;
q[++ tt] = 0;
for(int i = 1; i <= n; i ++)
{
while(h[q[tt]] >= h[i]) tt --;
l[i] = q[tt]+1;
q[++ tt] = i;
}
tt = -1;
q[++ tt] = n + 1;
for(int i = n; i; i --)
{
while(h[q[tt]] >= h[i]) tt --;
r[i] = q[tt]-1;
q[++ tt] = i;
}
ll res = 0;
for(int i = 1; i <= n; i ++) res = max(res,(ll)h[i]*(r[i]-l[i]+1));
printf("%lld\n", res);
}
return 0;
} 


三.升级题
一.Maximal submatrix

代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=5e3+7;
int mp[maxn][maxn];
int mark[maxn][maxn];
int h[maxn];
int q[maxn];
int l[maxn];
int r[maxn];
int n,m;
int solve(int h[]){
h[0]=h[m+1]=-1;
int tt=-1;
q[++tt]=0;
for(int i=1;i<=m;i++){
while(h[q[tt]]>=h[i]) tt--;
l[i]=q[tt]+1;
q[++tt]=i;
}
tt=-1;
q[++tt]=m+1;
for(int i=m;i;i--){
while(h[q[tt]]>=h[i]) tt--;
r[i]=q[tt]-1;
q[++tt]=i;
}
int res=0;
for(int i=1;i<=m;i++){
res=max(res,h[i]*(r[i]-l[i]+1));
}
return res;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
}
}
for(int j=1;j<=n;j++){
mark[1][j]=1;
for(int i=2;i<=n;i++){
if(mp[i][j]>=mp[i-1][j]){
mark[i][j]=mark[i-1][j]+1;
}else{
mark[i][j]=1;
}
}
}
int ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,solve(mark[i]));
}
cout<<ans<<'\n';
}
system("pause");
return 0;
}二. 与上题类似

这个题就是维护一个h[i][j]和l[i][j]和r[i][j],最后的答案就是max(h[i][j]*(r[i][j]-l[i][j]+1)),按上一道题做法也行。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e3+100;
char s[maxn][maxn];
int a[maxn][maxn];
int up[maxn][maxn];
int l[maxn][maxn];
int r[maxn][maxn];
int q[maxn];
int main(){
int n,m;
cin>>n>>m;
for (int i = 1; i <= n; i ++ ){
for(int j=1;j<=m;j++){
cin>>s[i][j];
if(s[i][j]=='F'){
a[i][j]=1;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]){
up[i][j]=up[i-1][j]+1;
}
else{
up[i][j]=0;
}
}
}
for(int i=1;i<=n;i++){
int tt=-1;
up[i][0]=up[i][m+1]=-1;
q[++tt]=0;
for(int j=1;j<=m;j++){//维护单调递增的栈
while(up[i][j]<=up[i][q[tt]]) tt--;
l[i][j]=q[tt]+1;
q[++tt]=j;
}
tt=-1;
q[++tt]=m+1;
for(int j=m;j>=1;j--){
while(up[i][q[tt]]>=up[i][j]) tt--;
r[i][j]=q[tt]-1;
q[++tt]=j;
}
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//cout<<i<<" "<<j<<" "<<l[i][j]<<" "<<r[i][j]<<" "<<up[i][j]<<endl;
ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);
}
}
cout<<ans*3<<endl;
}三.移动列
给你一个二进制矩阵 matrix ,它的大小为 m x n ,你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后,全是 1 的子矩阵面积。
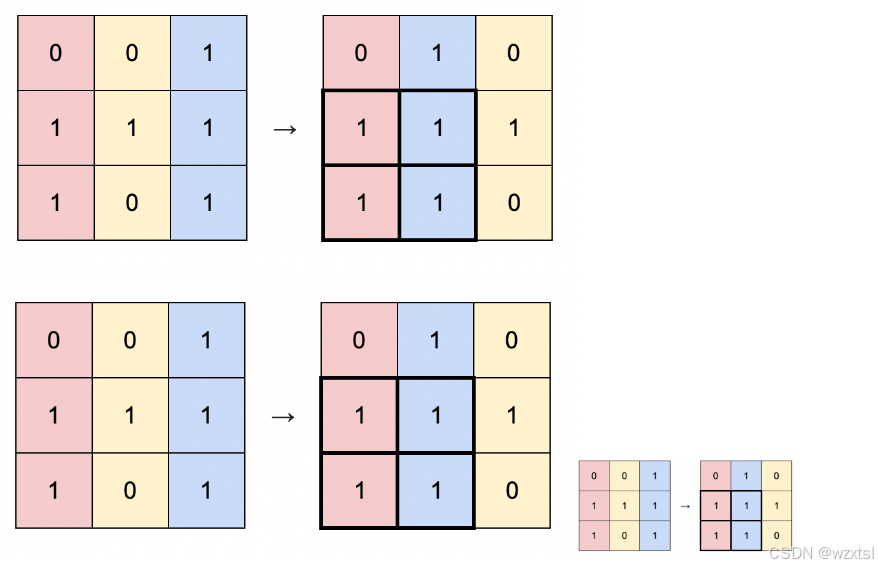
示例1:
输入:matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 4 。
示例 2:
输入:matrix = [[1,0,1,0,1]]
输出:3
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 3 。
示例 3:
输入:matrix = [[1,1,0],[1,0,1]]
输出:2
解释:由于你只能整列整列重新排布,所以没有比面积为 2 更大的全 1 子矩形。
示例 4:
输入:matrix = [[0,0],[0,0]]
输出:0
解释:由于矩阵中没有 1 ,没有任何全 1 的子矩阵,所以面积为 0 。
提示:
m == matrix.length
n == matrix[i].length
1 <= m * n <= 105
matrix[i][j] 要么是 0 ,要么是 1 。
这个题比上一个还简单就是维护一个h[i][j],他说可以交换任意列的次序,那么你在遍历每一列的时候拍个序就行;
class Solution {
public:
int largestSubmatrix(vector<vector<int>>& w) {
int n=w.size(),m=w[0].size();
for(int i=1;i<n;i++){
for(int j=0;j<m;j++){
if(w[i][j]){
w[i][j]+=w[i-1][j];
}
}
}
int ans=0;
vector<int>q(m);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
q[j]=w[i][j];
}
sort(q.begin(),q.end(),greater<int>());
for(int j=0;j<m;j++){
ans=max(ans,q[j]*(j+1));
}
}
return ans;
}
};单调栈这一算法虽迟但到,完结撒花!!!