2021国赛:和与乘积
题目描述
给定一个数列
,问有多少个区间[L,R] 满足区间内元素的乘积等于他们的和,即
输入描述
输入第一行包含一个整数 n,表示数列的长度。
第二行包含 n 个整数,依次表示数列中的数 a1,a2,⋯,an。
输出描述
输出仅一行,包含一个整数表示满足如上条件的区间的个数。
输入输出样例
输入
4 1 3 2 2输出
6样例解释
符合条件的区间为 [1,1],[1,3],[2,2],[3,3],[3,4],[4,4]。
评测用例规模与约定
对于 20% 的评测用例,n≤3000;
对于 50% 的评测用例,n≤20000;
对于所有评测用例,1≤n≤200000,1≤ai≤200000。
题目大意
给定一个数列,求有多少个子区间,它们的区间和与区间积相等。
1、简单做法:暴力法
构造前缀和以及前缀积的数组,来进行判断
暴力法的局限:乘积过大,寻找区间超时
2、贪心法
观察数据范围
对于所有评测用例,1≤ n ≤200000,1 ≤ai ≤200000。
所有元素之和最大只能到4*10^10
36个2相乘就会超过4*10^10,如果有数比2大,乘积只会更大。
因此,满足和与积相等的区间,非1的数字一定不会超过35个。
数字1的特性:
可以在不改变区间积的条件下改变区间和
解题思路
- 选出序列中不为1的数,每次选取最多不超过35个,计算这些数的区间和与区间积
- 如果区间积>区间和,计算当前区间左右两边的1的个数,判断能否通过补l的方式来使得区间和=区间积
- 通过计算补1的个数,就可以计算出使得当前和=积的区间个数,累计入总结果
- 对所有不为1的数全部判断完后,最终累计的总结果即为答案
下面对第一、三步进行详细说明:
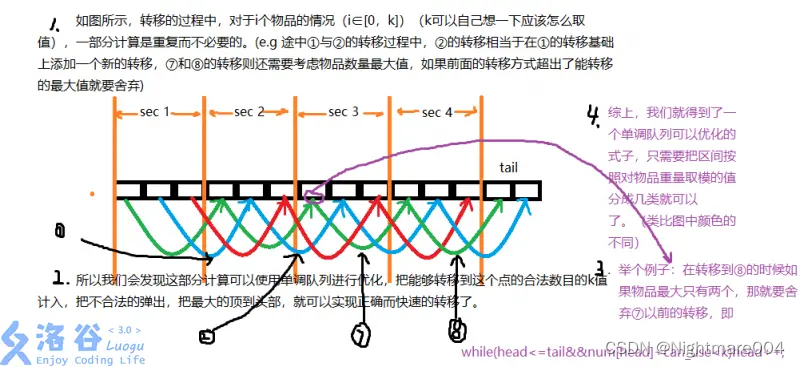
1、选出序列中不为l的数,每次选取最多不超过3个,计算这些数的区间和与区间积
index:—个队列deque(),记录每个非1的数的下标,算完一个就把它从队列移出。
S:前缀和数组
选数方式:
- 取出当前index队列头,以它为基准,不断往后判断,直到第35个数为止(队列不足35个数就到最后一个为止)
- 对于选出的每个区间,可以利用index计算出前缀和,区间乘积,以及两侧1的个数(左侧0的个数:当前非0数的下标 - 左侧第一个非0数的下标 - 1,右侧0的个数:右侧第一个非0数的下标 - 当前非0数的下标 - 1)
例如:a:[0,1,1,5,1,3,2,4,1,7,1,99,1,1](第一个数用0占位),那么index:(3, 5, 6, 7, 9, 11),两侧1的个数可以利用下标查计算,第一个非0数下标是index[1]=3,找到他左边第一个非0的数是a[0]=0,左边非0的个数=3-0-1=2,右边非0的个数=5-3-1=1。
3、通过计算补1的个数,就可以计算出使得当前和=积的区间个数,累计入总结果
left:左侧1的数量,right:右侧1的数量
两侧1的数量多的记为large,两侧1的数量少的记为small
delt:积-和
分类讨论
1、0 ≤ delt ≤ small
左侧补0个1,右侧补 delt个1;
左侧补一个1,右侧补delt-1个1;
以此类推,到最后一种是左侧补delt个1,右侧补0个1。
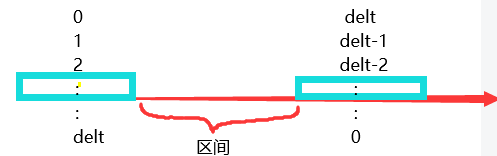
总共有delt+1种情况。
2、small < delt ≤ large
small区间最多补small个1,large区间没有限制,因为delt≤large。只需要考虑small区间,small区间补1的范围是0~small个,所以有small+1种情况。
3、large< delt < small + large
左右两侧区间都没有限制,small区间补1的范围是delt-large~small个,区间情况数:samll+large-delt-1
时间复杂度:O(n)
代码 (版本1)
from collections import deque
n = int(input())
a = [0] + list(map(int, input().split()))
big_1 = deque()
s = [0]
def count_num(delt, left, right): # 计算补1的区间情况数
small = min(left, right)
large = max(left, right)
if delt < 0 or delt > small + large:
return 0
elif delt <= small:
return delt + 1
elif delt <= large:
return small + 1
return small + large - delt + 1
for i in range(1, n + 1):
s.append(s[-1] + a[i]) # 计算区间和
if a[i] > 1:
big_1.append(i)
res = n - len(big_1) # 计算单独是1的区间
big_1.append(n + 1) # 判断最后一个时不需要特判
last_l = 0
# 计算非单独是1的区间
while len(big_1) > 1:
l = big_1[0] # 左端点从队列第一个开始
cmul = 1
for i in range(min(len(big_1) - 1, 36)): # 右端点遍历所有非0数/前35个非0数
r = big_1[i]·
cmul *= a[r] # 区间积
csum = s[r] - s[l - 1] # 区间和
if cmul >= csum: # 如果区间积>区间和
delt = cmul - csum # 积-和
cl = l - last_l - 1 # 左侧0的个数
cr = big_1[i + 1] - r - 1 # 右侧0的个数
res += count_num(delt, cl, cr)
last_l = l
big_1.popleft() # 弹出非0队列的队头
print(res)代码(版本2)
from collections import deque
def count(left, right, delt):
min, max = left, right
if min > max:
min, max = max, min
total = left + right
if delt < 0 or delt > total:
return 0
if delt <= min:
return delt + 1
if delt >= max:
return total - delt + 1
return min + 1
sum = [0]
s = lambda l, r: sum[r] - sum[l - 1] #匿名函数算区间和
index = deque()
if __name__ == '__main__':
n = int(input())
a = [None] + [int(x) for x in input().split()]
for i in range(1, n + 1):
sum.append(sum[-1] + a[i])
if a[i] > 1:
index.append(i)
ans = n - len(index)
index.append(n + 1)
last_l = 0
while len(index) > 1:
l = index[0]
p = 1
upper = min(len(index) - 1, 36) # number of not 1 < 36
for i in range(upper):
r = index[i]
r_next = index[i + 1]
p *= a[r]
delt = p - s(l, r) #中间的1已经在s(l,r)里算出来了,只要看两边的1
left = l - last_l - 1
right = r_next - r - 1
ans += count(left, right, delt)
last_l = l
index.popleft()
print(ans)