背包问题学习

news2025/2/25 13:03:57

01背包

01背包（0-1 Knapsack Problem）
有 N N N件物品和一个容量为 V V V的背包。放入第 i i i件物品耗费的费用是 C i C_i Ci​,得到的价值为 W i W_i Wi​。求解将哪些物品装入背包可以使价值总和最大

设 F [ i , v ] F\left[i,v\right] F[i,v]表示前 i i i件物品敲好放入一个容量为 v v v的背包可以获得的最大价值，容易写出
F [ i , v ] = max ⁡ { F [ i − 1 , v ] , F [ i − 1 , v − C i ] + W i } F\left[i,v\right] = \max\left\{F\left[i-1, v\right], F\left[i-1, v - C_i\right]+W_i\right\} F[i,v]=max{F[i−1,v],F[i−1,v−Ci​]+Wi​}
F [ 0 , 0 ] = 0 F\left[0,0\right] = 0 F[0,0]=0
时间复杂度 O ( N V ) O\left(NV\right) O(NV)

初始化

初始化有两种，一种是全 0 0 0，一种是 − ∞ -\infty −∞
如果题目要求敲好装满，就初始化 − ∞ -\infty −∞
如果只是要求最大，就初始化 0 0 0

代码

当然，这个代码容易MLE
洛谷P2871

#include<cstdio>
#include<algorithm>
const int N = 3405;
const int M = 12885;
int dp[N][M];

int main() {
	int n, m, w, d;
	scanf("%d%d", &n, &m);

	for (int i = 1; i <= n; ++i) {
		scanf("%d%d", &w, &d);
		for (int j = 1; j < w; ++j) {
			dp[i][j] = dp[i - 1][j];
		}
		for (int j = w; j <= m; ++j) {
			dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w] + d);
		}
	}
	printf("%d\n", dp[n][m]);


	return 0;
}

优化

虽然时间复杂度没法优化，但是空间复杂度可以

容易发现，我们只用到了上一行的状态，因此，我们最多需要两行数组
此时如果从后往前更新，我们就只需要用一行数组

如果你从前往后更新，相当于你放了好几次物品 i i i,这样就不是01背包了

洛谷P2871

#include<cstdio>
#include<algorithm>
const int M = 12885;
int dp[M];

int main() {
	int n, m, w, d;
	scanf("%d%d", &n, &m);

	for (int i = 0; i < n; ++i) {
		scanf("%d%d", &w, &d);
		for (int j = m; j >= w; --j) {
			dp[j] = std::max(dp[j], dp[j - w] + d);
		}
	}
	printf("%d\n", dp[m]);


	return 0;
}

完全背包问题

01背包（Complete Knapsack Problem）

有 N N N件物品和一个容量为 V V V的背包。放入第 i i i件物品耗费的费用是 C i C_i Ci​,得到的价值为 W i W_i Wi​，每件物品可以无限使用，求解将哪些物品装入背包可以使价值总和最大

如果沿用01背包的思路，容易写出
f [ i , v ] = max ⁡ { f [ i − 1 , v − k C i ] + k W i ∣ 0 ≤ k C i ≤ v } f\left[i,v\right] = \max\left\{f\left[i-1, v - kC_i\right] + kW_i \mid 0\le kC_i \le v\right\} f[i,v]=max{f[i−1,v−kCi​]+kWi​∣0≤kCi​≤v}
但是这样大概的时间复杂度 O ( N V ∑ V C i ) O\left(NV\sum \frac{V}{C_i}\right) O(NV∑Ci​V​)

F [ i , v ] = max ⁡ { F [ i − 1 , v ] , F [ i , v − C i ] + W i } F\left[i,v\right] = \max\left\{F\left[i-1, v\right], F\left[i, v - C_i\right]+W_i\right\} F[i,v]=max{F[i−1,v],F[i,v−Ci​]+Wi​}
时间复杂度 O ( N V ) O\left(NV\right) O(NV)

代码

洛谷P1616

#include<cstdio>
#include<algorithm>

const int M = 1e7 + 5;
long long dp[M];

int main() {
	int t, m, a, b;
	scanf("%d%d", &t, &m);

	for (int i = 0; i < m; ++i) {
		scanf("%d%d", &a, &b);
		for (int j = a; j <= t; ++j) {
			dp[j] = std::max(dp[j], dp[j - a] + b);
		}
	}
	printf("%lld\n", dp[t]);
	return 0;
}

多重背包

有 N N N件物品和一个容量为 V V V的背包。第 i i i件物品最多有 M i M_i Mi​件可用，放入第 i i i件物品耗费的费用是 C i C_i Ci​,得到的价值为 W i W_i Wi​。求解将哪些物品装入背包可以使价值总和最大

同样，容易写出
f [ i , v ] = max ⁡ { f [ i − 1 , v − k C i ] + k W i ∣ 0 ≤ k ≤ min ⁡ { M i , ⌊ v C i ⌋ } } f\left[i,v\right] = \max\left\{f\left[i-1, v - kC_i\right] + kW_i \mid 0\le k \le \min\left\{M_i,\left\lfloor\frac{v}{C_i}\right\rfloor\right\}\right\} f[i,v]=max{f[i−1,v−kCi​]+kWi​∣0≤k≤min{Mi​,⌊Ci​v​⌋}}
不过时间复杂度 O ( V ∑ M i ) O\left(V\sum M_i\right) O(V∑Mi​)

二进制优化

如果 C i M i ≥ V C_i M_i \ge V Ci​Mi​≥V，则这个物品可以按照完全背包处理

一个数 m m m可以分解为 1 , 2 , 4 , ⋯   , 2 k − 1 , m − ( 2 k − 1 ) 1,2,4,\cdots,2^{k-1},m-\left(2^{k} -1\right) 1,2,4,⋯,2k−1,m−(2k−1)
其中 k k k满足 m − ( 2 k − 1 ) > 0 m-\left(2^k - 1\right)>0 m−(2k−1)>0
这些数可以组合成 [ 1 , m ] \left[1,m\right] [1,m]中的任何数

也就是说我们可以把 m i m_i mi​拆分，然后做01背包
时间复杂度 O ( V ∑ log ⁡ 2 M i ) O\left(V\sum \log_2 M_i\right) O(V∑log2​Mi​)

代码

洛谷P1776

#include<cstdio>
#include<algorithm>

const int M = 4e4 + 5;
int dp[M], W;

void complete_knapsack(int w, int v) {
	for (int j = w; j <= W; ++j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void zero_one_knapsack(int w, int v) {
	for (int j = W; j >= w; --j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

int main() {
	int n, v, w, m;
	scanf("%d%d", &n, &W);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &v, &w, &m);
		if (w * m >= W) {//完全背包
			complete_knapsack(w, v);
		}
		else { //二进制拆分, 转为01背包
			int k = 1, temp_w = w, temp_v = v;
			while (k < m) {
				zero_one_knapsack(temp_w, temp_v);
				m -= k;
				temp_w += temp_w;
				temp_v += temp_v;
				k += k;
			}
			//剩余
			w = m * w;
			v = m * v;
			zero_one_knapsack(w, v);
		}
	}
	printf("%d\n", dp[W]);
	return 0;
}

单调队列优化

在这里插入图片描述
f [ i , v ] = max ⁡ { f [ i − 1 , v − k C i ] + k W i ∣ 0 ≤ k ≤ min ⁡ { M i , ⌊ v C i ⌋ } } f\left[i,v\right] = \max\left\{f\left[i-1, v - kC_i\right] + kW_i \mid 0\le k \le \min\left\{M_i,\left\lfloor\frac{v}{C_i}\right\rfloor\right\}\right\} f[i,v]=max{f[i−1,v−kCi​]+kWi​∣0≤k≤min{Mi​,⌊Ci​v​⌋}}

v = k 1 C i + d ,   k 1 = ⌊ v C i ⌋ ,   d = v m o d C i v = k_1C_i +d,\ k_1 = \left\lfloor\frac{v}{C_i}\right\rfloor,\ d = v \mathop{mod}C_i v=k1​Ci​+d, k1​=⌊Ci​v​⌋, d=vmodCi​
则
f [ i , k 1 C i + d ] = max ⁡ { f [ i − 1 , k 1 C i + d − k C i ] + k W i } = max ⁡ { f [ i − 1 , d + ( k 1 − k ) C i ] − ( k 1 − k ) W i } + k 1 W i \begin{aligned} f\left[i,k_1C_i +d\right] &= \max\left\{f\left[i-1, k_1C_i +d - kC_i\right] + kW_i \right\}\\ &= \max\left\{f\left[i-1, d + \left(k_1 - k\right)C_i \right] - \left(k_1-k\right)W_i \right\} + k_1 W_i\\ \end{aligned} f[i,k1​Ci​+d]​=max{f[i−1,k1​Ci​+d−kCi​]+kWi​}=max{f[i−1,d+(k1​−k)Ci​]−(k1​−k)Wi​}+k1​Wi​​
将 k 1 − k k_1 - k k1​−k替换一下

f [ i , k 1 C i + d ] = max ⁡ { f [ i − 1 , d + k C i ] − k W i ∣ max ⁡ { 0 , k 1 − M i } ≤ k ≤ k 1 } + k 1 W i f\left[i,k_1C_i +d\right] = \max\left\{f\left[i-1, d+kC_i\right] -kW_i\mid \max\left\{0,k_1 - M_i\right\}\le k \le k_1\right\}+k_1W_i f[i,k1​Ci​+d]=max{f[i−1,d+kCi​]−kWi​∣max{0,k1​−Mi​}≤k≤k1​}+k1​Wi​
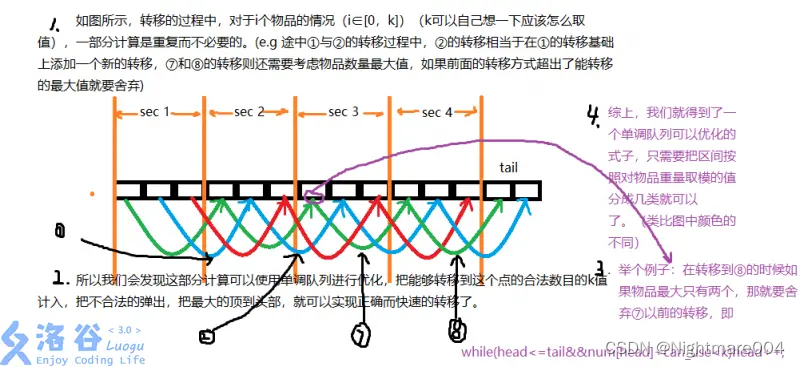
也就是说我们要维护一个窗口内的最大值，可以考虑用单调队列
枚举 d d d, 每次变化 k 1 k_1 k1​和 k k k，变化 k 1 k_1 k1​时，维护窗口 [ k 1 − M i , k 1 ] \left[k_1-M_i,k_1\right] [k1​−Mi​,k1​]的最大值

在固定 d d d的情况下， k 1 k_1 k1​至多有 ⌊ V − d C i ⌋ \left\lfloor\frac{V-d}{C_i}\right\rfloor ⌊Ci​V−d​⌋种
而 d d d有 C i C_i Ci​种，这样总的复杂度就是 O ( V ) O\left(V\right) O(V)

#include<cstdio>
#include<algorithm>

const int M = 4e4 + 5;
int dp[M], W;
int q1[M], q2[M], head, tail;//单调递减队列，q1存下标，q2存值

int main() {
	int n, v, w, m, ans = 0;
	scanf("%d%d", &n, &W);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &v, &w, &m);
		if (w == 0) {//防止除以0
			ans += m * v;
			continue;
		}
		for (int d = 0; d < w; ++d) {//枚举余数d
			head = 1;
			tail = 0;
			int max_k = (W - d) / w;
			int window_size = std::min(m, W / w);
			for (int k1 = 0; k1 <= max_k; ++k1) {
				int cur = dp[d + k1 * w] - k1 * v;
				while (head <= tail && cur >= q2[tail]) --tail;
				q1[++tail] = k1;
				q2[tail] = cur;
				//k1 - window_size <= k <= k1
				while (head <= tail && q1[head] < k1 - window_size)++head;
				dp[d + k1 * w] = std::max(dp[d + k1 * w], q2[head] + k1 * v);
			}
		}
	}
	printf("%d\n", ans + dp[W]);
	return 0;
}

混合背包

就是01背包，完全背包，多重背包结合，

做法就是判断每个物品属于哪种背包
洛谷P1833
我这里多重背包用的单调队列优化的
似乎二进制优化也可以过

#include<cstdio>
#include<algorithm>

const int M = 1005;
int dp[M], W;
int q1[M], q2[M], head, tail;

void complete_knapsack(int w, int v) {
	for (int j = w; j <= W; ++j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void zero_one_knapsack(int w, int v) {
	for (int j = W; j >= w; --j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void multi_knapsack(int w, int v, int m) {
	//需要保证w不为0
	for (int d = 0; d < w; ++d) {//枚举余数d
		head = 1;
		tail = 0;
		int max_k = (W - d) / w;
		int window_size = std::min(m, W / w);
		for (int k1 = 0; k1 <= max_k; ++k1) {
			int cur = dp[d + k1 * w] - k1 * v;
			while (head <= tail && cur >= q2[tail]) --tail;
			q1[++tail] = k1;
			q2[tail] = cur;
			//k1 - window_size <= k <= k1
			while (head <= tail && q1[head] < k1 - window_size)++head;
			dp[d + k1 * w] = std::max(dp[d + k1 * w], q2[head] + k1 * v);
		}
	}
}

int main() {
	int nx, ny, ex, ey, n;
	scanf("%d:%d%d:%d%d", &nx, &ny, &ex, &ey, &n);
	W = (ex * 60 + ey) - (nx * 60 + ny);
	int t, c, p, ans = 0;
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &t, &c, &p);
		if (t == 0) {
			//应该没有这种情况
			//if (p == 0) ans = 0x7fffffff;
			ans += c * p;
		}
		else if (p == 0 || t * p >= W) {//完全背包
			complete_knapsack(t, c);
		}
		else if (p == 1) {//01背包
			zero_one_knapsack(t, c);
		}
		else {
			multi_knapsack(t, c, p);
		}
	}
	printf("%d\n", ans + dp[W]);
	return 0;
}

二维费用的背包问题

设第 i i i件物品所需的两种费用为 C i C_i Ci​和 D i D_i Di​，两种费用可付出的最大值（背包容量）分别为 V , U V,U V,U，物品价值为 W i W_i Wi​，问怎样选择物品可以得到最大的价值

设 F [ i , v , u ] F\left[i,v,u\right] F[i,v,u]表示前 i i i件物品付出两种费用分别为 v v v和 u u u时可获得的最大价值，于是
F [ i , u , v ] = max ⁡ { F [ i − 1 , v , u ] , F [ i − 1 , v − C i , u − D i ] + W i } F\left[i,u,v\right] = \max \left\{F\left[i-1,v,u\right], F\left[i-1,v-C_i,u-D_i\right] + W_i\right\} F[i,u,v]=max{F[i−1,v,u],F[i−1,v−Ci​,u−Di​]+Wi​}

代码

洛谷P1855
这里价值为1

#include<cstdio>
#include<algorithm>

const int V = 205;
const int U = 205;

int dp[V][U];

int main() {
	int n, M, T, m, t;
	scanf("%d%d%d", &n, &M, &T);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d", &m, &t); // 价值为1
		for (int j = M; j >= m; --j) {
			for (int k = T; k >= t; --k) {
				dp[j][k] = std::max(dp[j][k], dp[j - m][k - t] + 1);
			}
		}
	}
	printf("%d\n", dp[M][T]);
	return 0;
}

分组的背包问题

有 N N N件物品和一个容量为 V V V的背包。第 i i i件物品的费用时 C i C_i Ci​，价值是 W i W_i Wi​。这些物品被划分为 K K K组，每组中的物品互相冲突，最多选一件。求解将哪些物品装入背包可使这些物品的费用综合不超过背包容量，且价值最大

这个问题其实就相当于每一组中，选一件，还是一件都不选
设 F [ k , v ] F\left[k,v\right] F[k,v]表示前 k k k组物品花费费用 v v v能取得的最大权值，则
F [ k , v ] = max ⁡ { F [ k − 1 , v ] , F [ k − 1 , v − C i ] + W i ∣ i t e m   i ∈ g r o u p   k } F\left[k,v\right] = \max\left\{F\left[k-1,v\right], F\left[k-1,v-C_i\right] + W_i \mid item\ i \in group\ k\right\} F[k,v]=max{F[k−1,v],F[k−1,v−Ci​]+Wi​∣item i∈group k}
循环的时候，先循环 V V V再循环组内物品

代码

洛谷P1757

#include<cstdio>
#include<algorithm>

const int N = 1005;
const int M = 1005;

int w[N];
int v[N];
int g[N][N];//g[i][j]表示第i组第j个物品是g[i][j]
int cnt[N];//cnt[i]表示第i组有几个物品
int dp[M];

int main() {
	int m, n, c, max_group = 0;
	scanf("%d%d", &m, &n);

	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &w[i], &v[i], &c);
		g[c][cnt[c]] = i;
		++cnt[c];
		max_group = std::max(max_group, c);
	}
	for (int i = 0; i <= max_group; ++i) {
		if (cnt[i] == 0)continue;
		for (int j = m; j >= 0; --j) {
			for (int k = 0; k < cnt[i]; ++k) {
				int idx = g[i][k];
				if (w[idx] <= j) {
					dp[j] = std::max(dp[j], dp[j - w[idx]] + v[idx]);
				}
			}
		}
	}
	printf("%d\n", dp[m]);
	return 0;
}

有依赖的背包问题

物品 i i i依赖于物品 j j j，即，选了物品 i i i就必须选物品 j j j（但是选了物品 j j j不一定要选物品 i i i）

简化版

只有一层依赖，并且没有循环依赖

一般版

没有循环依赖，但是有多层依赖

树形dp，从叶子一层一层向上
相当于先跑孩子的，然后孩子里跑一遍01背包，最后加上当前节点

代码

acwing10

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int MAXN = 105;
const int MAXV = 105;

vector<int> edge[MAXN];
int dp[MAXN][MAXV], V;
int v[MAXN];
int w[MAXN];

void dfs(int u) {
	for (int i = 0; i < edge[u].size(); ++i) {
		int son = edge[u][i];
		dfs(son);
		for (int j = V - v[u]; j >= 0; --j) {//遍历除去当前节点体积后的所有体积
			for (int k = j; k >= 0; --k) {//遍历决策
				dp[u][j] = std::max(dp[u][j], dp[u][j - k] + dp[son][k]);
			}
		}
	}
	for (int i = V; i >= v[u]; --i) {//加上当前节点
		dp[u][i] = dp[u][i - v[u]] + w[u];
	}
	for (int i = v[u] - 1; i >= 0; --i) {//装不下当前节点，方案不可行
		dp[u][i] = 0;
	}
}

int main() {
	int p, root, N;
	scanf("%d%d", &N, &V);
	for (int i = 1; i <= N; ++i) {
		scanf("%d%d%d", &v[i], &w[i], &p);
		if (p != -1)edge[p].push_back(i);
		else root = i;

	}
	dfs(root);
	printf("%d\n", dp[root][V]);
	return 0;
}

洛谷P1064
这里因为都是10的倍数，所以可以同时除以10，不然会T

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 65;
const int M = 3.2e3 + 5;

vector<int> edge[N];

int dp[N][M], m;
int w[N];
int v[N];

void dfs(int u) {
	for (int i = 0; i < edge[u].size(); ++i) {
		int son = edge[u][i];
		dfs(son);
		for (int j = m - w[u]; j >= 0; --j) {
			for (int k = j; k >= 0; --k) {
				dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[son][k]);
			}
		}
	}
	for (int i = m; i >= w[u]; --i) {
		dp[u][i] = dp[u][i - w[u]] + v[u];
	}
	for (int i = w[u] - 1; i >= 0; --i) {
		dp[u][i] = 0;
	}
}

int main() {
	int n, q;
	scanf("%d%d", &m, &n);
	m /= 10;
	for (int i = 1; i <= n; ++i) {
		scanf("%d%d%d", &w[i], &v[i], &q);
		w[i] /= 10;
		v[i] *= w[i];
		edge[q].push_back(i);
	}
	dfs(0);
	printf("%d\n", dp[0][m] * 10);
	return 0;
}

泛化物品

再背包容量为 V V V的背包问题中，泛化物品时一个定义域为 0 , ⋯   , V 0,\cdots, V 0,⋯,V中的整数的函数 h h h，当分配给他的费用为 v v v时，能得到的价值就是 h ( v ) h\left(v\right) h(v)

例如01背包就是 h ( v ) = { w , v = c 0 , o t h e r w i s e h\left(v\right) = \begin{cases} w, & v = c\\ 0, & otherwise\\ \end{cases} h(v)={w,0,​v=cotherwise​

再说…

其他

输出具体方案

以01背包为例

用二维的数组
如果不要求字典序，可以考虑从右下角开始
如果 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]，那么说明没有用物品 i i i，就向上走
否则使用了物品 i i i，则跳到 d p [ i − 1 ] [ j − w [ i ] ] dp[i-1][j-w[i]] dp[i−1][j−w[i]]

最后一直跳到 d p [ 0 ] [ 0 ] dp[0][0] dp[0][0]

另一种是使用二维bool数组
dp的时候，如果不使用物品 i i i， g [ i ] [ j ] = f a l s e g[i][j] = false g[i][j]=false,否则 g [ i ] [ j ] = t r u e g[i][j] = true g[i][j]=true
剩下的就是跟上面一样

字典序：
逆序存物品，输出的时候再变换回来

代码

acwing12

#include<cstdio>

const int MAXN = 1005;
const int MAXM = 1005;

int dp[MAXM], V;
bool g[MAXN][MAXM];
int v[MAXN];
int w[MAXN];

int main() {
	int N;
	scanf("%d%d", &N, &V);
	for (int i = N; i >= 1; --i) {
		scanf("%d%d", &v[i], &w[i]);
	}
	for (int i = 1; i <= N; ++i) {
		for (int j = V; j >= v[i]; --j) {
			int temp = dp[j - v[i]] + w[i];
			if (temp >= dp[j]) {
				dp[j] = temp;
				g[i][j] = true;
			}
		}
	}

	bool flag = false;
	int x = N, y = V;
	while (x > 0) {
		if (g[x][y]) {
			y -= v[x];
			if (flag) {
				printf(" ");
			}
			else {
				flag = true;
			}
			printf("%d", N - x + 1);
		}
		--x;
	}
	printf("\n");
	return 0;
}

求方案总数

把之前的 max ⁡ \max max,换成 s u m sum sum

求最优方案总数

设 f [ i ] [ j ] f[i][j] f[i][j]为只能放前 i i i个物品的情况下，容量为 j j j的背包正好装满所能到达的最大价值
g [ i ] [ j ] g[i][j] g[i][j]为只能放前 i i i个物品的情况下，容量为 j j j的背包正好装满的方案数

代码

acwing11

#include<cstdio>
#include<cstring>
#include<algorithm>

const int M = 1005;
const int mod = 1e9 + 7;

int dp[M], V;
int g[M] = { 1 };

int main() {
	memset(dp, 0xc0, sizeof(dp));
	dp[0] = 0;
	int N, v, w;
	scanf("%d%d", &N, &V);
	for (int i = 0; i < N; ++i) {
		scanf("%d%d", &v, &w);
		for (int j = V; j >= v; --j) {
			int temp = std::max(dp[j], dp[j - v] + w);
			int cnt = 0;
			if (dp[j] == temp) cnt = (cnt + g[j]) % mod;
			if (dp[j - v] + w == temp)cnt = (cnt + g[j - v]) % mod;
			dp[j] = temp;
			g[j] = cnt;
		}
	}
	int ans = 0;
	for (int i = 0; i <= V; ++i) {
		ans = std::max(ans, dp[i]);
	}
	int res = 0;
	for (int i = 0; i <= V; ++i) {
		if (dp[i] == ans)res = (res + g[i]) % mod;
	}
	printf("%d\n", res);
	return 0;
}

第 k 优解

再说

参考：
https://github.com/tianyicui/pack

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/191011.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

软件防错设计

软件防错设计

出现非预期错误的原因解决方案原理介绍断根原理原理&#xff1a;将可能造成人错误的原因/条件从根本上排除断绝掉。通过冗余设计&#xff0c;屏蔽掉其中9种错误的方式&#xff1b;案例&#xff1a;USB的SD卡防写开关。4种可能性断根设计为只有1种可能是正确的。软件设计&#x…
阅读更多...
Linux学习之环境准备【Vm+Centos】

Linux学习之环境准备【Vm+Centos】

文章目录前言一 VMware Workstation17 Pro下载和安装1.1 Vm下载指南1.2 VM安装指南二 Centos7安装2.1 装机器2.2 装系统三 补充内容3.1 卸载Centos前言 工欲善其事&#xff0c;必先利其器&#xff0c;我们要学习Linux当然需要Linux的环境由于大部分人使用的是Windows系统无法进…
阅读更多...
介绍OAuth2

介绍OAuth2

目录 一、什么是OAuth2&#xff1f; 二、OAuth2中的角色 1、资源所有者 2、资源服务器 3、客户 4、授权服务器 三、认证流程 四、OAuth2授权方式 注&#xff1a;使用令牌方式的优点 1、授权码 2、隐藏方式 3、密码方式 4、凭证方式 一、什么是OAuth2&#xff1f…
阅读更多...
深入浅出ConcurrentHashMap1.8

深入浅出ConcurrentHashMap1.8

前言 HashMap是我们平时开发过程中用的比较多的集合&#xff0c;但它是非线程安全的&#xff0c;在涉及到多线程并发的情况&#xff0c;进行get操作有可能会引起死循环&#xff0c;导致CPU利用率接近100%。 final HashMap<String, String> map new HashMap<String,…
阅读更多...
基于Springboot搭建java项目（二十四）——权限认证框架SpringSecurity

基于Springboot搭建java项目（二十四）——权限认证框架SpringSecurity

权限认证框架SpringSecurity 一、为什么要做权限认证 在WEB开发的过程当中&#xff0c;安全一直是很重要的一方面。安全和直接的业务是没有直接挂钩的&#xff0c;但是在业务实现的初期如果没有考虑的安全性的化&#xff0c;在后期迭代的时候就会出现很多的问题。例如存在着安…
阅读更多...
4.1--贪心--活动安排问题

4.1--贪心--活动安排问题

今天开始&#xff0c;快速过一遍贪心&#xff0c;贪心要比动态规划简单许多&#xff0c;但是&#xff0c;我们也要理解其中的证明过程 贪心算法采用自顶向下&#xff0c;以迭代的方法做出相继的贪心选择&#xff0c;每做一次贪心选择就将所求问题简化为一个规模更小的子问题&am…
阅读更多...
Maven实战-3.setting.xml标签说明

Maven实战-3.setting.xml标签说明

前言 持续更新中… setting.xml文件 1.<localRepository> 自定义本地Maven仓库目录地址。 这样本地的仓库地址就是配置的目录了。 2.<proxies> 基于安全因素考虑&#xff0c;使用通过安全认证的代理访问因特网&#xff0c;这时候需要为Maven配置HTTP代理&…
阅读更多...
TOOM大数据舆情监控系统方案，如何做好舆情大数据监测分析?

TOOM大数据舆情监控系统方案，如何做好舆情大数据监测分析?

大数据舆情监控是指通过对大量数据的收集、分析和处理&#xff0c;了解舆论的发展趋势和活动&#xff0c;并对舆论风险进行预警和评估&#xff0c;以保障企业的舆论安全。TOOM大数据舆情监控系统方案&#xff0c;如何做好舆情大数据监测分析? 一、大数据舆情监控系统方案 1.…
阅读更多...
车载以太网 - SomeIP - SomeIP Entry - 04

车载以太网 - SomeIP - SomeIP Entry - 04

前面总纲内容有说，车载以太网中的SomeIP内容是非常多的，并且为了实现SOA的相关需求，提供了多种多样的报文类型，因此也就有了今天要说的SomeIP-SD中的重要组成部分之一的条目（Entry）部分，而SomeIP-SD在车载网络中占有相当大的比重，可以当做是一定要实现的，如果这块不实…
阅读更多...
C语言知识点复习------排序法(冒泡、选择、插入)与链表

C语言知识点复习------排序法(冒泡、选择、插入)与链表

目录 排序 冒泡排序&#xff1a; 选择排序&#xff1a; 插入排序&#xff1a; 链表 单链表的建立 单向循环链表的建立 双向循环链表 排序 冒泡排序&#xff1a; 冒泡排序&#xff08;Bubble Sort&#xff09;也是一种简单直观的排序算法。它重复地走访过要排序的数列&a…
阅读更多...
RK356X系列（RK3568）GL857L芯片 USB驱动开发

RK356X系列（RK3568）GL857L芯片 USB驱动开发

首先我们先区分一下USB几种控制器类型协议 OHCI UHCI EHCI xHCI。OHCI、UHCI都是USB1.1的接口标准&#xff0c;而EHCI是对应USB2.0的接口标准&#xff0c;最新的xHCI是USB3.0的接口标准。1. OHCI&#xff08;Open Host Controller Interface&#xff09;是支持USB1.1的标准&…
阅读更多...
C++ | 数据结构与算法 | 单源最短路径 | Dijkstra Bellman Ford

C++ | 数据结构与算法 | 单源最短路径 | Dijkstra Bellman Ford

文章目录前言Dijkstra算法讲解与实现Bellman Ford算法与实现前言 &#xff08;关于代码实现的图结构&#xff0c;可以看图结构的实现这篇文章&#xff09; Dijkstra的实现与Prim的实现相似&#xff0c;两者都是通过贪心思想实现&#xff0c;它们有什么不同呢&#xff1f;首先…
阅读更多...
数字IC设计工程师一般都干什么

数字IC设计工程师一般都干什么

数字IC设计工程师一般都干什么 简单来说&#xff0c;数字IC设计工程师一般就是负责写verilog代码&#xff08;当然&#xff0c;不是仅仅写个代码&#xff09;。本文主要对数字IC设计的工作流程进行简单的介绍&#xff0c;也算是对我从业一年来的总结。 一般来说&#xff0c;数…
阅读更多...
linux下的僵尸进程处理SIGCHLD信号

linux下的僵尸进程处理SIGCHLD信号

阅读目录 对于waitpid的p i d参数的解释与其值有关&#xff1a;wait与waitpid区别&#xff1a; 转自&#xff1a;linux下的僵尸进程处理SIGCHLD信号 - Jessica程序猿 - 博客园 什么是僵尸进程&#xff1f; 首先内核会释放终止进程(调用了exit系统调用)所使用的所有存储区&am…
阅读更多...
Java——字母大小写全排列

Java——字母大小写全排列

题目链接 字母大小写全排列 题目描述 给定一个字符串 s &#xff0c;通过将字符串 s 中的每个字母转变大小写&#xff0c;我们可以获得一个新的字符串。 返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。 题目示例 输入&#xff1a;s “a1b2” 输出&#xff1a…
阅读更多...
spring-boot国际化i18n中英文实现

spring-boot国际化i18n中英文实现

一、背景 接触到的项目&#xff0c;使用国际化越来越多&#xff0c;系统页面实现中英文环境&#xff0c;记录下&#xff0c;前端使用vue vue-i8n 后端java自己封装 前端翻译对象&#xff1a;页面涉及到的所有按钮&#xff08;包括新增、删除、导出、下载、导入、上一页、下…
阅读更多...
相控阵天线分析综合、设计与测试

相控阵天线分析综合、设计与测试

目录概述HFSS特殊曲线天线建模直线阵列天线特性和阵列因子&#xff08;方向图乘积定理、波束扫描&#xff09;非规则直线阵列天线&#xff08;稀布阵列、稀疏阵列、平方率分布阵列&#xff09;直线阵列天线低副瓣综合&#xff08;切比雪夫、泰勒分布、SinZ-Z和Villeneuve分布&a…
阅读更多...
2023-java面试最新总结

2023-java面试最新总结

1. Java中的原始数据类型都有哪些&#xff0c;它们的大小及对应的封装类是什么&#xff1f; boolean boolean数据类型非true即false。这个数据类型表示1 bit&#xff0c;但是它的大小并没有精确定义。 《Java虚拟机规范》中如是说&#xff1a;“虽然定义了boolean这种数据类型…
阅读更多...
胡歌官宣生女，胡椒粉们真为他高兴，人生最顶级的能力是【涅槃重生】的力量

胡歌官宣生女，胡椒粉们真为他高兴，人生最顶级的能力是【涅槃重生】的力量

今天刷到胡歌官宣生女&#xff0c;胡歌当父亲了&#xff0c;真为他高兴。恭喜老胡&#xff01;&#x1f389;作为十多年胡椒粉&#xff0c;连夜录制了这个视频&#xff08;抖音视频号&#xff1a;【小伍说_523的作品】胡歌官宣生女&#xff0c;十几年的胡椒粉真替他高兴&#x…
阅读更多...
Unity二

Unity二

一、脚本的创建 可以在project视图中的Assets文件夹中右键创建一个C#脚本&#xff0c;可以将脚本分类放在不同的文件夹中&#xff0c;或者点击游戏对象后在Inspector视图中找到最下方的添加组件按钮&#xff0c;然后点击新建脚本即可。若在project视图中创建的脚本&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023