C++·栈和队列

栈和队列是什么看这里：

数据结构·栈和队列-CSDN博客文章浏览阅读948次，点赞25次，收藏26次。本节讲解了栈和队列的内容，其核心就是栈的特点是后进先出，队列的特点是先进先出。并用C语言实现了栈和队列的结构以及它们的各种接口https://blog.csdn.net/atlanteep/article/details/136071056?spm=1001.2014.3001.5501

准确的来说栈和队列并不是一种容器，而是容器适配器，可以看到他们的第二个参数传的都不是空间配置器，而是另一个东西。不过因为第二个参数是一个缺省参数，因此这并不影响我们正常使用他们。

1. stack 栈

官网资料：stack - C++ Reference

这是栈的所有成员函数，emplace我们先不关心，其他成员函数我们都懂是什么意思。

其中top就是取栈顶元素，会返回栈顶元素的引用。

swap交换两个栈中的元素。

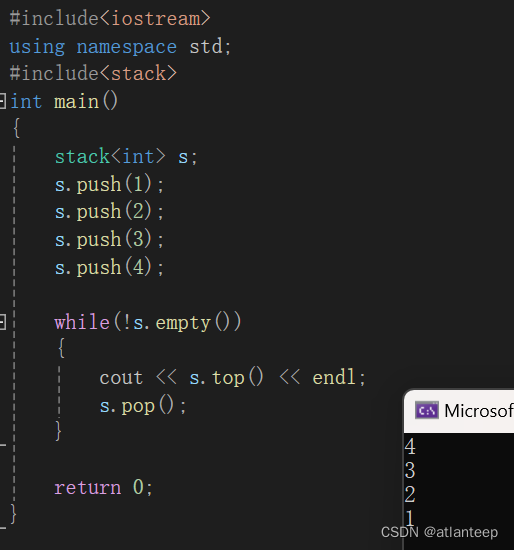
可以看到，非常的后进先出。

2. queue 队列

官网资料：queue - C++ Reference

成员函数：

栈和队列成员函数都一样，只是队列中用front返回队头的引用

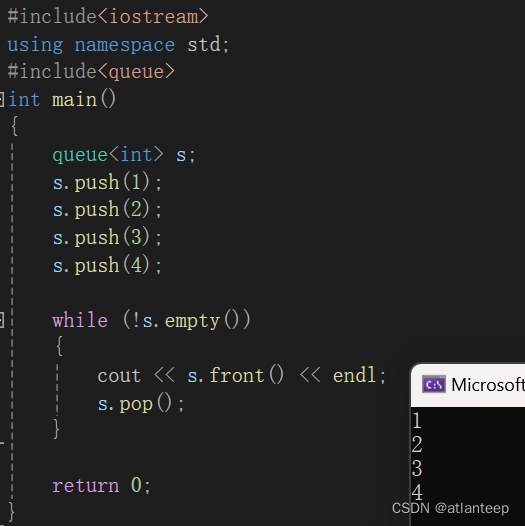
可以看到，非常的先进先出。

3. 容器适配器

一开始我们提到过栈和队列都是容器适配器，这个容器适配器的功能就是不用我们自己手动去实现栈和队列，而是借助其他容器进行生成。比如果我们在顺序表外套一层外壳，让这个容器只支持尾插尾删，那不就相当于将顺序表适配成了栈。

3.1 容器适配器使用

当然在实际写栈的时候我们不能将栈的底层写死成顺序表，因为链表或别的容器结构也可以当作栈的底层。

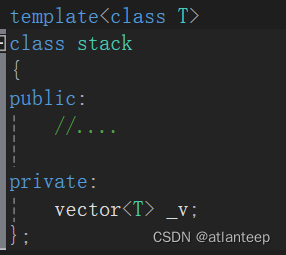
为了解决这一问题，我们可以在添加一个模板参数Container

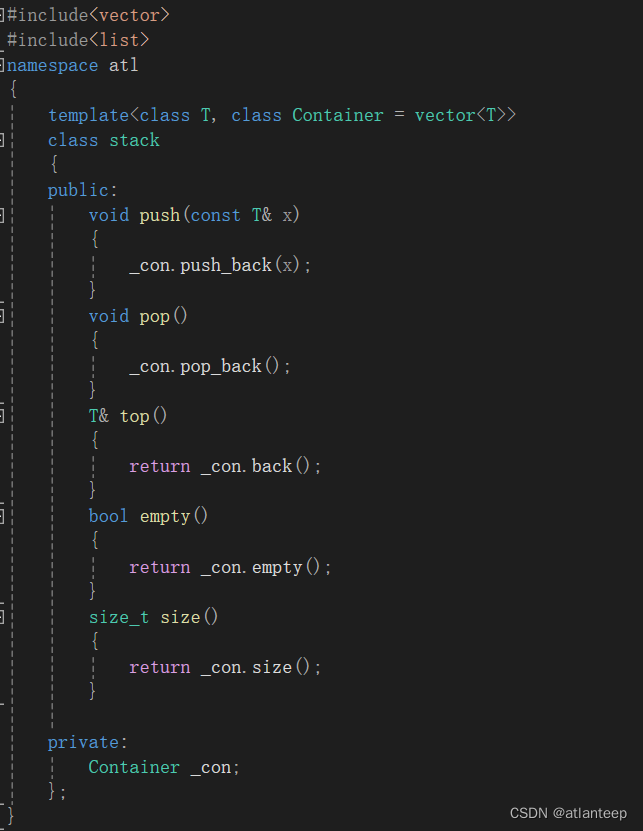
然后用这个位置的容器生成它的对象，再用这个对象的操作函数来完善整个stack。首先明确一点，就是因为成员变量是自定义类型，因此我们不用写stack的构造函数等，因为电脑会自动生成这些函数，调用自定义类型中的构造函数来构造stack类型。

因此我们直接实现stack的各种功能

当然，如果 _con 这个容器不支持比如 push_back pop_back 这些操作，那生成的栈的时候就会报错，说明这个容器无法适配。

可以看到，我们将一个数据结构封装之后就形成了一个新的数据结构，可以体会一下这个过程。

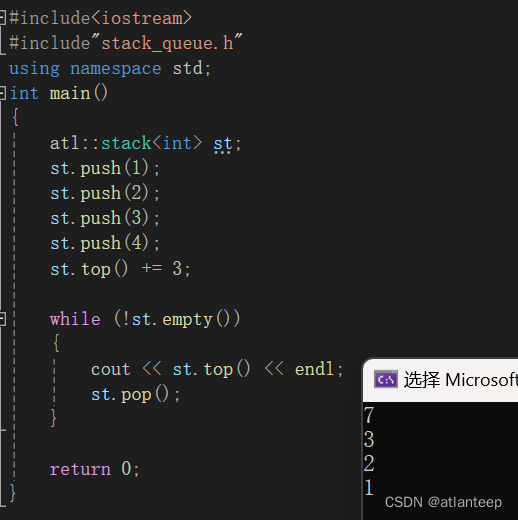
下面我们验证一下自己写的栈：

那么在STL库中模板参数被给到一个缺省值 deque<T> ，模板参数也是参数因此我们也可以给我们自己写的模板加上缺省值，这样就可以不给第二个模板参数了

3.2 deque<T> 双端队列

官网资料：deque - C++ Reference

可以看到，list链表没有的 [ ] 访问，vector顺序表没有的 _front 修改，在deque双端队列中同时都被支持了，所以说deque是list和vector的结合体。

3.2.1 deque的原理介绍

deque首先是有一个中控数组，中控数组中的每个元素都是一个数组指针，指向各个buffer(缓冲)数组，deque容器中的数据内容都存储在buffer数组中。这样的话deque容器就同时包含了连续存储和链式存储的两个特点了。

如果想要头插数据，就在头创建个buff数组，用中控数组将新buffer数组和旧数组统一维护进deque容器中，也就是说只用给中控数扩容头插一下，从而避免了像vector那样头插数据时要将后面的所有数据都向后挪动。

当想查找元素的时候，比如，如果buffer数组长度都统一成10，我们想查找第25个元素的内容是什么，25/10得出所在第几个buffer数组，25%10得出在此buffer数组的第几位上。

当然，看到这里大家就肯定已经能发现deque容器结构的诸多弊端了：1. 如果在容器中间insert一个数据的时候后面的所有数据要不要挪动，还是将所处buffer数组扩容；2. 那如果各个buffer数组的长度不同，[ ] 查找元素的时候将要一个一个的统计buffer数组长度，最后才能找到元素处在第几个buffer数组，这样的话 [ ] 下标访问操作的速度远不及vector的访问速度；3. 与list容器排序时拥有同样的问题，就是当 [ ] 下标访问效率不高的情况下，给容器中数据排序时的效率也会及低。

ps: 这里提醒一下，算法库中的sort要求传随机迭代器，而list容器是双向迭代器，因此在给list容器内容排序时，只能用list容器自己的成员函数，不过值得放心的是deque是随机迭代器。

但是deque也有自己的优势，它的头插头删效率远高于vector，因为支持 [ ] 因此数据访问也比list快一点，所以当我们需要大量头插头删少量数据元素访问时，deque就是不错的选择，也就是说stack和queue使用deque当默认适配器就很不错。

4. priority_queue 优先级队列

官网资料：priority_queue - C++ Reference

优先级队列不是一个队列，只是这个名字这么叫的，priority_queue会保证第一个数据永远是优先级最高的数据。

priority_queue的底层是一个堆，我们观察它的三个模板参数，第一个指示优先级队列中存储数据的类型，第二个参数因为底层是堆，所以用vector来适配，第三个参数是一个仿函数，它的缺省参数保证了这个堆是大根堆。

这是priority_queue的所有成员函数，和stack与queue的很类似。

这里要提醒一下，在构造容器的时候不止可以使用迭代区间来构造，当源是数组的时候我们可以直接使用原生指针，只要是连续的空间就可以这么构造。

这里我们给迭代区间或者原生指针区间构造的话，priority_queue就直接去建堆了。

我们可以从调试中看出来，把数据一股脑放进去然后priority_queue直接就是建堆了。

如果我们把第三个模板参数改成great仿函数就是建小堆

这里我们可以联系堆排序来记忆，sort算法中，less仿函数作为缺省参数用来排升序，排升序建大根堆；greater相反排降序，降序建小根堆。

在C++中没用专门的堆结构，因为可以说优先级队列就是堆，所以当我们需要使用堆的时候去使用priority_queue就可以了。

4.1 priority_queue 的实现

仿函数的问题我们一会再说，现在先不用仿函数，把优先级队列的适配框架化出来

关于堆的结构以及建堆等问题详见：数据结构·二叉树(一)_生成4个4层的满二叉树r1, r2, r3, r4,然后把4颗树的根节点串起来-CSDN博客文章浏览阅读1k次，点赞24次，收藏23次。本节介绍了二叉树的概念，基于完全二叉树引出了堆的概念，并着手实现了一个小根堆，最后我们介绍了堆应用中的堆排序和TOP-K问题，堆排序的时间复杂度是跟快排一个量级的，很有意思_生成4个4层的满二叉树r1, r2, r3, r4,然后把4颗树的根节点串起来https://blog.csdn.net/atlanteep/article/details/136437696

4.1.1 push pop

push一个一个数据的插入建堆，用到向上调整算法建堆

pop删除堆顶数据要先将堆顶和最后一个数据调换位置，删掉调换后的最后一个数据，再把现在的堆顶元素向下调整落位。

我这个pop的写法有点麻烦，还是用二叉树那节里的假设法简单一点

4.1.2 top size empty

4.1.3 迭代区间构造

这里我们先一股脑把数据都存进_con顺序表中，然后向下建堆，而不选择一个一个数据存进去向上建堆，毕竟O(N)与O(N*logN)的差距还是有的。

因为写了一种构造了，所以编译器不会自动生成默认构造了，于是我们用第一行代码强制让编译器生成默认构造。

4.2 仿函数

到这里优先级队列的实现就基本完成了，但是还有一个缺陷没解决，就是我们现在写的这个只能建大堆，太死板了，因此下面我们下面要通过仿函数来彻底解决这一问题。

4.2.1 基本概念

仿函数，也叫函数对象，它是一个重载了圆括号 operator() 的类，类的对象可以像函数一样使用。

比如上面这段代码，我们重载了 () 操作符之后，让Func实例化出来的f1对象使用这个重载了的操作符，就使得这个对象看起来像是一个函数名，整个操作看起来就像是使用了一个传参了的函数。

4.2.2 仿函数应用

下面我们写一个自己的less仿函数，给它加上模板参数，用来适配多种类型变量的比较

我们知道C语言中的qsort函数，是通过传函数指针来确定排升序还是降序的，但是C++中并不喜欢用函数指针，而是用仿函数取而代之，而priority_queue的第三个参数，也就是那个仿函数就起到了与qsort中那个函数指针类似的作用。

下面我们实现一下代码，需要修改的位置只有3个地方，就是容器模板，向上调整的比较规则和向下调整的比较规则。

下面我们测试一下可不可行

很明显，仿函数的使用成功起到应有的作用了。

4.3 priority_queue实现代码

template<class T>
class my_less
{
public:
	bool operator()(const T& x, const T& y)
	{
		return x < y;
	}
};

template<class T>
class my_greater
{
public:
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};

template<class T, class Container = vector<T>, class Compare = my_less<T>>
class priority_queue
{
public:
	priority_queue() = default;
	template<class InputIterator>
	priority_queue(InputIterator first, InputIterator last)
	{
		while (first != last)
		{
			_con.push_back(*first);
			++first;
		}
		//建堆算法
		//最后一个非叶子节点
		int parent = (_con.size() - 2) / 2;
		while (parent >= 0)
		{
			adjustdown(parent);
			--parent;
		}
	}

	void adjustup(int child)
	{
		Compare compfunc;
		int parent = (child - 1) / 2;
		while (child > 0)
		{
			//默认建大堆
			//if (_con[parent] < _con[child])
			if (compfunc(_con[parent], _con[child]))
			{
				swap(_con[child], _con[parent]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
				break;
		}
	}
	void push(const T& x)
	{
		_con.push_back(x);
		adjustup(_con.size() - 1);
	}

	void adjustdown(int parent)
	{
		Compare compfunc;
		int l_child = parent * 2 + 1;
		int r_child = l_child + 1;
		int sz = _con.size() - 1;
		while (l_child <= sz)
		{
			if (r_child <= sz)//右孩子存在
			{
				//if (_con[l_child] < _con[r_child])
				if (compfunc(_con[l_child], _con[r_child]))
				{
					//右孩子大
					//if (_con[parent] < _con[r_child])
					if (compfunc(_con[parent], _con[r_child]))
					{
						swap(_con[r_child], _con[parent]);
						parent = r_child;
						l_child = parent * 2 + 1;
						r_child = l_child + 1;
						continue;
					}
				}
				//左孩子大
			}
			//只有左孩子
			//if (_con[parent] < _con[l_child])
			if (compfunc(_con[parent], _con[l_child]))
			{
				swap(_con[l_child], _con[parent]);
				parent = l_child;
				l_child = parent * 2 + 1;
				r_child = l_child + 1;
				continue;
			}
			//左右孩子都比父小
			break;
		}
	}
	void pop()
	{
		swap(_con[0], _con[_con.size() - 1]);
		_con.pop_back();  
		adjustdown(0);
	}

	const T& top()
	{
		return _con[0];
	}
	size_t size()
	{
		return _con.size();
	}
	bool empty()
	{
		return _con.empty();
	}

private:
	Container _con;
};