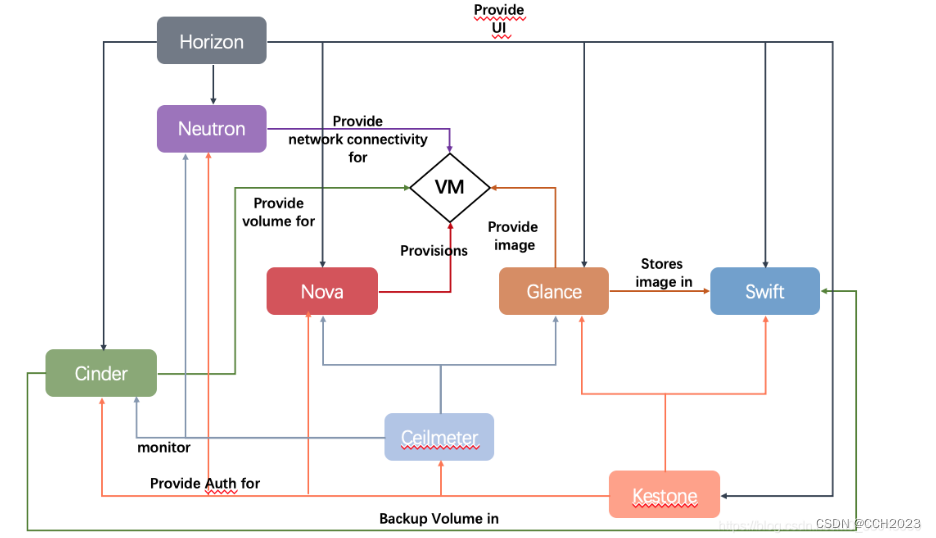
在CPU等对性能要求较高的电路中，一般都会采用超前进位加法器，因为超前进位加法器的延时相对来说比较小。下面讲述超前进位加法器的原理：
我们知道，一个三输入，二输出的全加器，其逻辑关系为

$$S=A\oplus B\oplus C_{in}$$

$$C_{out}=(A\&B)|(C_{in}\&(A\oplus B))$$
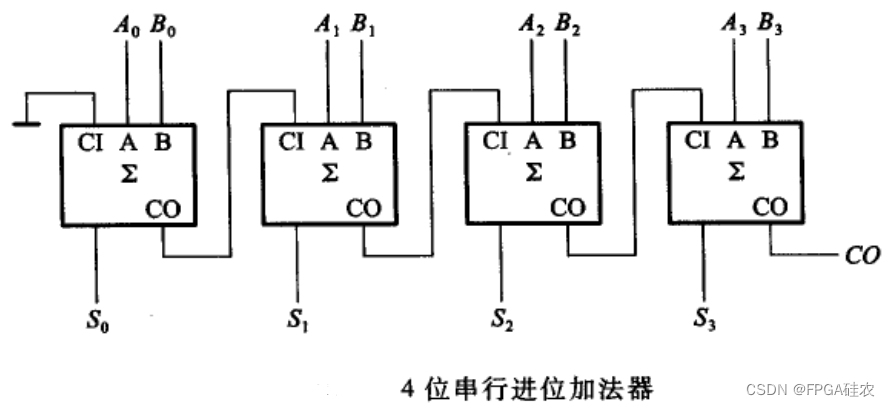
对于普通的级联的加法器，上一位的进位输出需要作为下一位的进位输入，因此，随着加法器位宽的增大，加法器的延时也会线性增大，如下图所示。究其原因，就是下一个比特位对上一个比特位的依赖造成的，超前进位加法器就是解决了这个问题，从而实现低延时的效果。

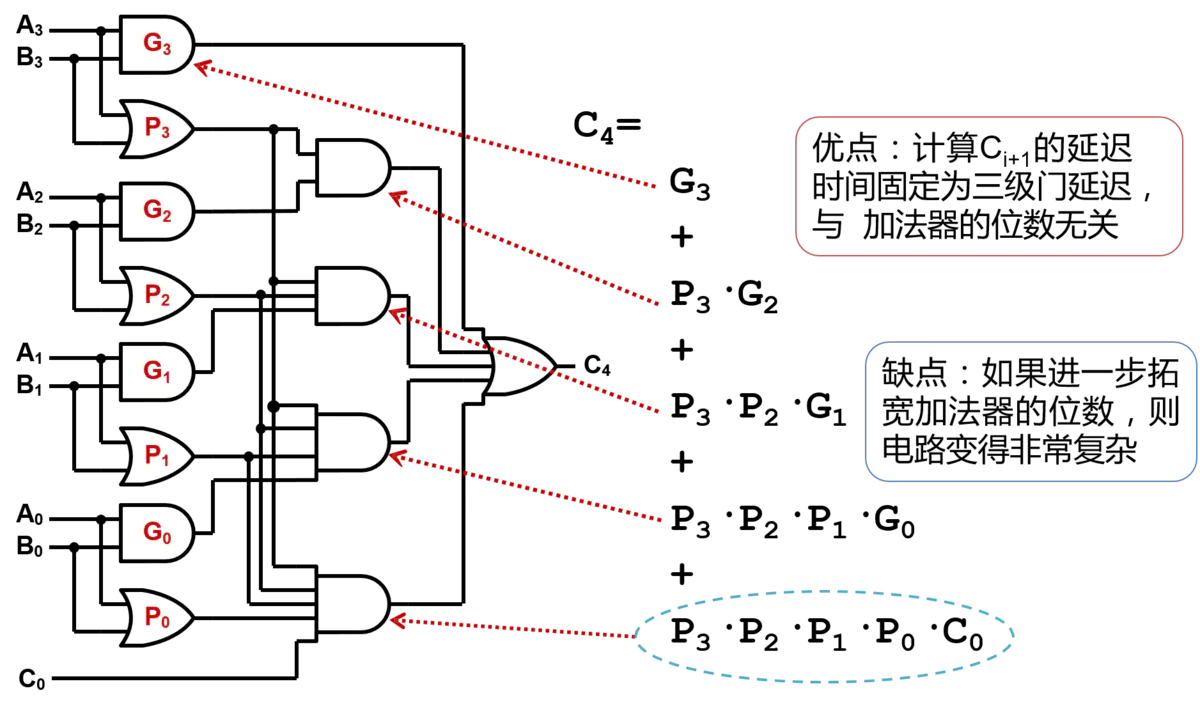
首先，我们有
$$C_{i+1}=A_i{B}_i+C_i(A_i+B_i)$$
该式子描述了第i+1位的进位输出和第i位的进位输出之间的关系，如果我们用
$$C_i=A_{i-1}{B}_{i-1}+C_{i-1}(A_{i-1}+B_{i-1})$$
代替上式中的$C_i$，则可以得到$C_{i+1}$和$C_{i-1}$之间的关系，进一步将$C_{i-1}$用$C_{i-2}$表示，一直迭代到$C_0$，即$C_{in}$，我们发现，此时进位输出不再依赖于前面任何一级加法器的结果，因此也就达到了我们要的效果。下图是一个4位超前进位加法器的示意图，由图可知，超前进位加法器的延迟是固定的，与加法器的位宽无关，因此超前进位加法器具有低延迟的优点，然后，从图中也不难发现，随着位宽的增大，与门的扇入也随之增大，因此电路也会变得更加复杂。在实际电路设计中，通过将两者(串行进位加法器、超前进位加法器)相结合，从而在延迟和电路复杂度间进行权衡。

下面是1个简单的4位超前进位加法器的Verilog代码实现：

module CLA(
input logic cin,
input logic [3:0] a,
input logic [3:0] b,
output logic cout,
output logic [3:0] sum
);
logic [4:0] c;
logic [3:0] g;
logic [3:0] p;
//
assign g=a&b;
assign p=a^b;
assign c[0]=cin;
assign cout=c[4];
//Cout=Gi+PiCin
assign c[1]=g[0]|(p[0]&c[0]);
assign c[2]=g[1]|(p[1]&(g[0]|(p[0]&c[0])));
assign c[3]=g[2]|(p[2]&(g[1]|(p[1]&(g[0]|(p[0]&c[0])))));
assign c[4]=g[3]|(p[3]&(g[2]|(p[2]&(g[1]|(p[1]&(g[0]|(p[0]&c[0])))))));
genvar i;
generate
    for(i=0;i<4;i++)begin:sum_block
        assign sum[i]=p[i]^c[i];
    end
endgenerate
endmodule

相应的测试平台为：

module test;
logic [3:0] a;
logic [3:0] b;
logic cin;
logic cout_ref;
logic cout;
logic [3:0] sum_ref;
logic [3:0] sum;
logic error;
initial
begin
   repeat(100)
   begin
      #10
      cin=$urandom%2;
      a=$urandom%16;
      b=$urandom%16;
   end
end
assign {cout_ref,sum_ref}=cin+a+b;
assign error=(sum!=sum_ref)?1'b1:1'b0;
initial begin
    #1000
    $finish;
end

initial begin
   $fsdbDumpfile("./out.fsdb");
   $fsdbDumpvars(0);
end

CLA u(.*);

endmodule

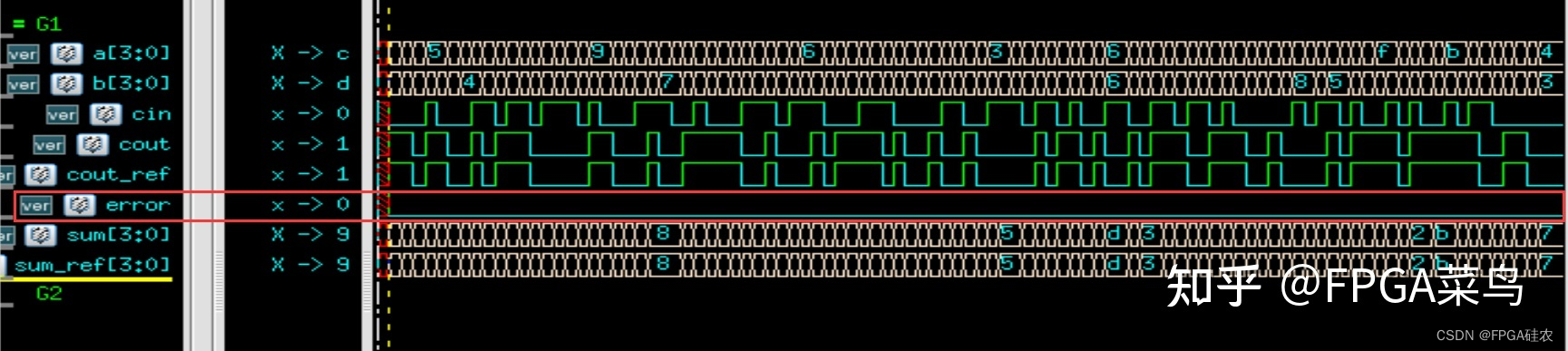
VCS仿真波形如下图所示，可以看到，代码是无误的。

【注】本博客搬运自本人知乎