Ceres Solver解算已知函数模型参数

news2025/2/27 1:45:19

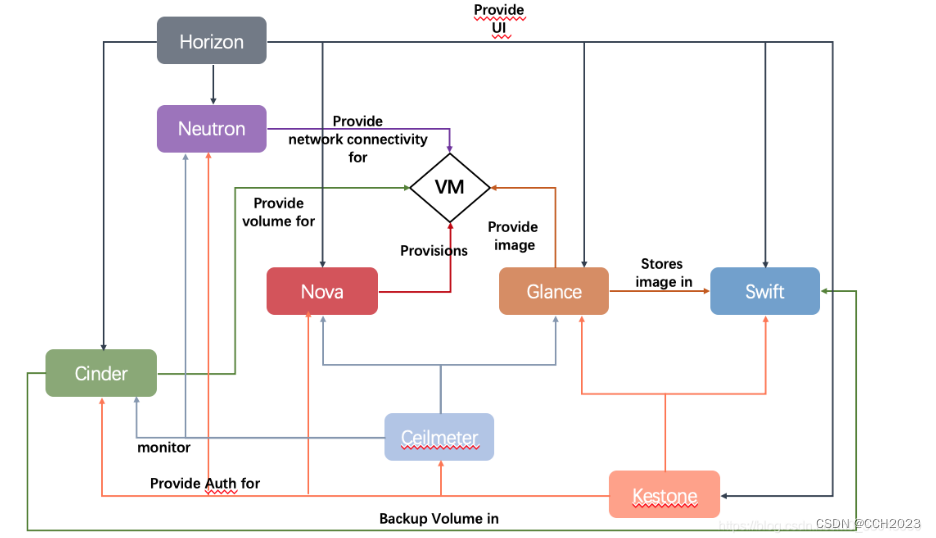
一、介绍

Ceres solver 是谷歌开发的一款用于非线性优化的库，在已知一个函数表达式，以及一组观测到的值，利用最小二乘是可以解算得到相关参数。下面举例使用ceres solver解算直线函数以及曲线函数参数。

其过程包括三个步骤：

（1）步骤一：构建代价函数

（2）步骤二：通过代价函数构建待求解的优化问题

（3）步骤三：配置求解器参数并求解。这个步骤不需要知道怎么求解，只要调用solver方法即可完成。

二、直线函数的求解

假如直线方程：，一组观测值[-1,-1; 1,5; 2,8; 3,11]

代码如下：

#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;
//y=3x+2
const int kNumObservations = 4;
// clang-format off
const double data[] = {
  -1.0, -1.0,
  1, 5,
  2, 8,
  3, 11,
 
};
//(1)构造代价函数
// clang-format on
//y=ax+b=3x+2
struct CostFunc_Line {
    CostFunc_Line(double x, double y) : x_(x), y_(y) {}
    template <typename T>
    bool operator()(const T* const a, const T* const b, T* residual) const {
        residual[0] = y_ - a[0] * x_ - b[0];
        return true;
    }
private:
    const double x_;
    const double y_;
};
int main(int argc, char** argv) {
   // google::InitGoogleLogging(argv[0]);
    double a = -1.0;
    double b = 0.0;
    Problem problem;
//(2)利用代价 函数构建优化问题
    for (int i = 0; i < kNumObservations; ++i) {
        problem.AddResidualBlock(
            new AutoDiffCostFunction<CostFunc_Line, 1, 1, 1>(
                new CostFunc_Line(data[2 * i], data[2 * i + 1])),
            nullptr,
            &a,
            &b);
    }
    Solver::Options options;
    options.max_num_iterations = 20;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;
    Solver::Summary summary;
   //(3)利用solver解算参数
    Solve(options, &problem, &summary);
    std::cout << summary.BriefReport() << "\n";
    std::cout << "Initial a: " << -1.0 << " b: " << 0.0 << "\n";
    std::cout << "Final   a: " << a << " b: " << b << "\n";
    system("pause");
    return 0;
}

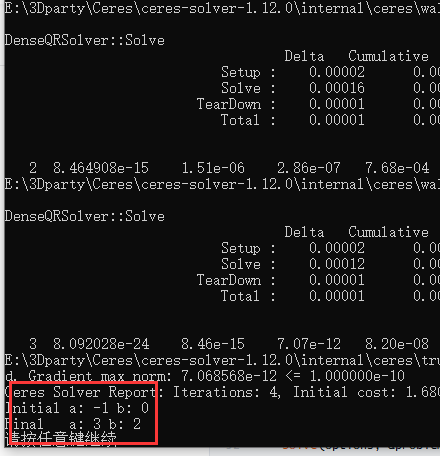
解算结果正确：a=3 b=2

三、抛物线解算参数

假如抛物线方程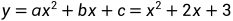：，对应的一组值为[-1,2; 0.5,4.25; 1,6; 2,11; 3,18;]

代码如下：

#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;
//y=3x+2
const int kNumObservations = 4;
// clang-format off
const double data[] = {
  -1.0, 2,
  0.5, 4.25,
  1, 6,
  2, 11,
  3,18
};
//(1)构建代价函数
// clang-format on
//y=ax^2+bx+c=x^2+2x+3
struct CostFunc_para_curve{
    CostFunc_para_curve(double x, double y) : x_(x), y_(y) {}
    template <typename T>
    bool operator()(const T* const a, const T* const b, const T* const c, T* residual) const {
        residual[0] = y_ - a[0] * x_ * x_ - b[0] * x_ - c[0];//函数
        return true;
    }
private:
    const double x_;
    const double y_;
};
int main(int argc, char** argv) {
   // google::InitGoogleLogging(argv[0]);
    double a = 0.0;
    double b = 0.0;
    double c = 0.0;
    Problem problem;
//（2）利用代价函数构建优化问题
    for (int i = 0; i < kNumObservations; ++i) {
        problem.AddResidualBlock(
            //4个参数
            new AutoDiffCostFunction<CostFunc_para_curve, 1, 1, 1,1>(
                new CostFunc_para_curve(data[2 * i], data[2 * i + 1])),
            nullptr,
            &a,
            &b,
            &c);//三个参数
    }
    Solver::Options options;
    options.max_num_iterations = 20;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;
    Solver::Summary summary;
//(3)利用solver解算参数
    Solve(options, &problem, &summary);
    std::cout << summary.BriefReport() << "\n";
    std::cout << "Initial a: " << 0.0 << " b: " << 0.0 << "c: " << 0.0 << "\n";
    std::cout << "Final   a: " << a << " b: " << b << " c: " << c << "\n";
    system("pause");
    return 0;
}

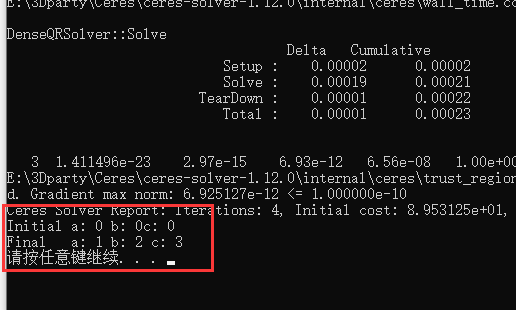
解算结果为：a=1 b=2 c=3

四、曲线

假设曲线方程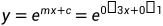,对应的一组值为[0,1.1051; 1,1.4918； 2,2.0137 3,2.71828；4,3.66926 ]

#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;
//y=e^(mx+c)=e^(0.3x+0.1)
const int kNumObservations = 5;
// clang-format off
const double data[] = {
 0,1.1051,
 1,1.4918,
 2,2.0137,
 3,2.71828,
 4,3.66926
};
//(1)构造代价函数
// clang-format on
//y=e^(mx+c)=e^(0.3x+0.1)
struct CostFunc_curve {
    CostFunc_curve(double x, double y) : x_(x), y_(y) {}
    template <typename T>
    bool operator()(const T* const m, const T* const c, T* residual) const {
        residual[0] = y_ - exp(m[0] * x_ + c[0]);
        return true;
    }
private:
    const double x_;
    const double y_;
};
int main(int argc, char** argv) {
    // google::InitGoogleLogging(argv[0]);
    double m = -1.0;
    double c = 0.0;
    Problem problem;
    //(2)利用代价 函数构建优化问题
    for (int i = 0; i < kNumObservations; ++i) {
        problem.AddResidualBlock(
            new AutoDiffCostFunction<CostFunc_curve, 1, 1, 1>(
                new CostFunc_curve(data[2 * i], data[2 * i + 1])),
            nullptr,
            &m,
            &c);
    }
    Solver::Options options;
    options.max_num_iterations = 20;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;
    Solver::Summary summary;
    //(3)利用solver解算参数
    Solve(options, &problem, &summary);
    std::cout << summary.BriefReport() << "\n";
    std::cout << "Initial m: " << -1.0 << " c: " << 0.0 << "\n";
    std::cout << "Final   m: " << m << " c: " << c << "\n";
    system("pause");
    return 0;
}

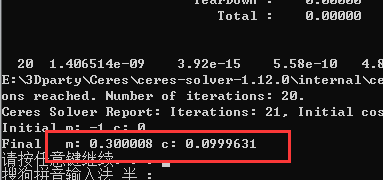
m=0.3 c=0.0999

小结：

相对来说，ceres解算已知函数模型，直接将观测值输入，利用solover函数解算即可，比较方便。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/190684.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

图为技术：专注核心技术 引领行业发展

图为技术：专注核心技术 引领行业发展

图为技术T-3D引擎经过多年的技术积累与原始创新&#xff0c;作为国内首批基于分布式技术进行三维图形底层渲染的开拓者&#xff0c;不仅在渲染架构上优势明显&#xff0c;同时其所具备数据管理能力也十分卓越。分布式架构采用独创的(Multi Compute Server To Web Render)架构方…
阅读更多...
Java多线程之CAS中的ABA问题与JUC的常见类

Java多线程之CAS中的ABA问题与JUC的常见类

文章目录一. CAS指令与ABA问题1. 解析CAS2. 基于CAS实现的原子类3. 基于CAS实现自旋锁4. ABA问题二. JUC中的常见类1. Callable接口2. ReentrantLock类(可重入锁)3. Semaphore类(信号量)4. CountDownLatch同步工具类一. CAS指令与ABA问题 1. 解析CAS CAS即compare and awap, …
阅读更多...
Cesium 坐标系的转换，空间数据加载 粒子系统加载

Cesium 坐标系的转换，空间数据加载 粒子系统加载

在vue中引入Cesium.js官网下载好的Cesium文件放入vue项目中index.html中引入,在js文件即可智能提示&#xff0c;或者下载依赖包也可<script src"./Cesium/Cesium.js"></script><link rel"stylesheet" href"./Cesium/Widgets/widgets.c…
阅读更多...
若依配置教程（六）Excel导入功能实现

若依配置教程（六）Excel导入功能实现

若依官网导入实现流程 文章目录一、前端index.vue中1.在所需模块的index.vue中的< script >< /script >中增加如下代码&#xff1a;2.在< template >< /template >中添加导入按钮事件&#xff1a;3.添加导入前端代码&#xff1a;二、在模块文件夹(ruoy…
阅读更多...
数学建模学习笔记（17）灰色预测模型和神经网络

数学建模学习笔记（17）灰色预测模型和神经网络

文章目录灰色预测模型相关基本概念GM(1,1)模型的使用步骤GM(1,1)模型的拓展模型GM(1,1)模型的注意事项BP神经网络预测模型的注意事项灰色预测模型 相关基本概念 系统的分类&#xff1a; 白色系统&#xff1a;系统的信息是完全明确的。灰色系统&#xff1a;系统的部分信息已知…
阅读更多...
readelf指令使用

readelf指令使用

一、指令说明readelf命令&#xff0c;一般用于查看ELF格式的文件信息&#xff0c;常见的文件如在Linux上的可执行文件&#xff0c;动态库(*.so)或者静态库(*.a) 等包含ELF格式的文件。以下命令的使用是基于android编译出来的so文件上面去运行。readelf常用命令语法&#xff1a;…
阅读更多...
视网膜电图特征可以检测成人的抑郁状态和治疗反应：一种机器学习方法

视网膜电图特征可以检测成人的抑郁状态和治疗反应：一种机器学习方法

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 视网膜电图特征可以检测成人的抑郁状态和治疗反应&#xff1a;一种机器学习方法摘要1. 引言2. 方法和材料2.1 人口与伦理声明2.2 入选标准、临床和生物学评估2.3 实验方案2.4…
阅读更多...
浅析代理IP与VPS

浅析代理IP与VPS

在跨境行业的热浪期&#xff0c;出海早已成为了企业发展的新趋势。像跨境电商&#xff0c;新媒体&#xff0c;旅游等行业都在开拓海外市场&#xff0c;越来越多的企业产生了匿名浏览互联网&#xff0c;隐藏真实IP的需求。能满足用户这一需求的方法有很多种&#xff0c;代理IP与…
阅读更多...
H264/AVC 句法和语义--重要的字段、带截图

H264/AVC 句法和语义--重要的字段、带截图

一 SPS、PPS句法和语义 宽高在SPS里。 profile_idc&#xff1a;baseline、main、high。 level_idc&#xff1a;值越大&#xff0c;最大宏块处理速率等值越大。 m_ptParam.i_level_idc 21; //X264编码参数 chroma_format_idc&#xff1a;1表示采样格式为4:2:0。 frame_mbs_onl…
阅读更多...
C++ 树进阶系列之平衡二叉查找树（ AVL）的自平衡算法

C++ 树进阶系列之平衡二叉查找树（ AVL）的自平衡算法

1. 前言 树的深度与性能的关系。 在二叉排序树上进行查找时&#xff0c;其时间复杂度理论上接近二分算法的时间复杂度O(logn)。 但是&#xff0c;这里有一个问题&#xff0c;如果数列中的数字顺序不一样时&#xff0c;构建出来的二叉排序树的深度会有差异性&#xff0c;对最…
阅读更多...
【Unity VR开发】结合VRTK4.0：抛物线

【Unity VR开发】结合VRTK4.0：抛物线

模块化开发&#xff08;抛物线&#xff09;&#xff1a; 当我们用久了一个固定的东西之后就不想去追求新的东西&#xff0c;其实这是一种懒惰&#xff0c;每个人都应该明白&#xff0c;每一天&#xff0c;这个时间都在发生着变化&#xff0c;不管是人、事、物&#xff0c;而我…
阅读更多...
[Android开发练习3] 四季图的切换

[Android开发练习3] 四季图的切换

前言 本题主要涉及到使用帧式布局&#xff0c;以及如何为组件设置点击的事件响应&#xff0c;包括获取事件源&#xff0c;设置事件监听器&#xff0c;在Activity文件中书写一般的业务逻辑代码。 文章目录 布局代码 text3_season.xml&#xff08;layout&#xff09; style.xm…
阅读更多...
私有云OpenStack学习笔记1

私有云OpenStack学习笔记1

私有云&#xff1a;自己组建私有云系统。 私有云系统有哪些呢&#xff1f; OpenStack、CloudStack、Eucalyptus、vCloud Director四大主流云平台。 云计算有极大的潜力提高效率&#xff0c;显著地节约成本&#xff0c;实现可升级的基础设施和高性能以及安全的数据存储。 Ope…
阅读更多...
秋招备战——Java基础知识

秋招备战——Java基础知识

垃圾回收&#xff0c;JVM常用参数 将内存中不再被使用的对象进行回收&#xff0c;GC中用于回收的方法称为收集器&#xff0c;由于GC需要消耗一些资源和时间&#xff0c;Java在对对象的生命周期特征进行分析后&#xff0c;按照新生代、老年代的方式来对对象进行收集&#xff0c…
阅读更多...
2023情人节送另一半什么好？四款适合送女友的数码好物分享

2023情人节送另一半什么好？四款适合送女友的数码好物分享

2023年情人节快到了&#xff0c;一个关于浪漫、惊喜并且充满爱意的节日&#xff0c;不少人都在烦恼送另一半什么好。而数码产品在日常生活中也是必不可少的存在&#xff0c;在此&#xff0c;我给大家整理了四款适合送女友的数码好物&#xff0c;一起来看看吧。 一、蓝牙耳机&a…
阅读更多...
操作系统权限提升(四)之系统错误配置-Tusted Service Paths提权

操作系统权限提升(四)之系统错误配置-Tusted Service Paths提权

系列文章 操作系统权限提升(一)之操作系统权限介绍 操作系统权限提升(二)之常见提权的环境介绍 操作系统权限提升(三)之Windows系统内核溢出漏洞提权 注&#xff1a;阅读本编文章前&#xff0c;请先阅读系列文章&#xff0c;以免造成看不懂的情况&#xff01;&#xff01;&am…
阅读更多...
这18张 Python 数据科学速查表，让你的代码能力飞起来

这18张 Python 数据科学速查表，让你的代码能力飞起来

数据科学是利用科学方法、流程、算法和系统从数据中提取价值的跨学科领域。数据科学家综合利用一系列技能&#xff08;包括统计学、计算机科学和业务知识&#xff09;来分析从网络、智能手机、客户、传感器和其他来源收集的数据。 目前在主流的数据科学领域一般有三大生态&…
阅读更多...
深入详解 二次移动平均法python

深入详解 二次移动平均法python

什么是 二次移动平均法 二次移动平均法&#xff0c;也称为指数加权移动平均法&#xff0c;是一种用于平滑时间序列数据的算法。 文章目录二次移动平均法逻辑Python代码实现第二种实现二次移动平均法的方式第三种卷积实现二次移动平均法二次移动平均法的应用场景二次移动平均法逻…
阅读更多...
Linux监控之prometheus学习

Linux监控之prometheus学习

目录 需要学习以及掌握的知识 第一步&#xff1a;安装准备 1、安装nginx 2、安装prometheus 2_1、解压&#xff1a;prometheus-2.0.0.linux-amd64.tar.gz 2_2、移动到安装目录 2_3、将Prometheus配置为系统服务 2_4、重新加载系统文件&#xff0c;使prometheus.service文…
阅读更多...
Linux字符设备、块设备的区别

Linux字符设备、块设备的区别

一、字符设备 字符设备就是在对某设备进行操作时&#xff0c;该设备的读取以字节为单位进行。字符设备的操作是通过linux系统直接调用驱动程序完成的&#xff0c;在驱动程序的上一层并没用文件系统。因此字符设备的特点如下&#xff1a; 1、以字节流的方式进行读写、一个字节一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023