---

另类加法

题目链接

思路：

本题可以通过位运算实现，具体实现如下：
两个数求和，其实就是 求和后当前位的数据+两个数求和的进位

求和后当前位的数据：
简便的计算方法就是两个数进行异或 00000001 ^ 00000010 -> 00000011
求和后进位的数据：
简便的计算方法就是两个数相与后左移一位 (00000010 & 00000010) << 1

根据上面的规则，我们来简单操作一下。
例如：
1 + 3；
00000001 + 00000011
求和后当前的数据位: 0000 0010；求和后进位的数据：0000 0010
因为当前数据位和进位都不为0，所以数据位要加上进位
求和后的数据位：0000 0000；求和后的进位：0000 0100
因为当前数据位和进位都不为0，所以数据位要加上进位
求和后的数据位：0000 0100；求和后的进位：0000 0000

当进位为0，那么就返回当前的数值位就是1+3的答案。

代码：

方法一：递归
class UnusualAdd {
  public:
    int addAB(int A, int B) {
        // write code here
        
        if (B == 0) return A;//当进位为0时，此时数值位就是所求答案。
        int a = A ^ B;//求和后当前位的数据
        int b = (A & B) << 1;//求和后进位的数据
        return addAB(a, b);//递归两个数进行相加，任意为0时截止
    }
};
方法二：循环
class UnusualAdd {
public:
    int addAB(int A, int B) {
        // write code here

        int digit=A^B;
        int carry=((A&B)<<1);

        while (carry!=0) {
            int tmpdigit=digit;
            int tmpcarry=carry;

            digit=tmpdigit^tmpcarry;
            carry=((tmpdigit&tmpcarry)<<1);
            
        }
        return digit;
    }
};

---

走方格的方案数

题目链接

思路：

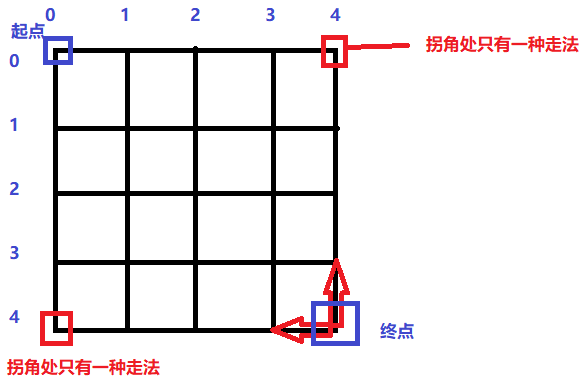
根据题意假设对于上面4*4的方格，就是从起点（0，0）到终点（4，4）有几种走法，我们从终点倒着往回推：

• 如果不是拐点（坐标n或者m都不为0），对于每一个这样的点（x，y），想回到起点的话就是（x-1，y）的方法数加上（x，y-1）的方法数。
  带入到本例中，对于坐标（4，4）那就是坐标（3，4）走到（0，0）的走法数加上坐标（4，3）走到（0，0）的走法数；对于（3，4）那就是（2，4）和（3，3）走到起点的方法数
• 如果遇到拐点（n或者m有一个为0即为拐点），则只有一种走法，横着往左走或者竖着往上走，返回1即可。

代码：

#include<iostream>
using namespace std;
int pathNum(int n, int m) {
    if(n==0||m==0)//遇到拐点
    {
        return 1;
    }
    
    return pathNum(n - 1, m) + pathNum(n, m - 1);//不是拐点
}

int main() {
    int n, m;
    while (cin >> n >> m) {
        cout << pathNum(n, m) << endl;
    }
    return 0;
}

---

end