【数据结构】（C语言）：二叉搜索树（不使用递归）

news2024/11/16 0:27:57

二叉搜索树：

  • 非线性的，树是层级结构。
  • 基本单位是节点，每个节点最多2个子节点。
  • 有序。每个节点，其左子节点都比它小，其右子节点都比它大。
  • 每个子树都是一个二叉搜索树。每个节点及其所有子节点形成子树。
  • 可以是空树。

C语言实现：（使用链表实现，不使用递归）

 创建结构体数据类型（记录二叉搜索树的根节点和数据个数）：

typedef struct Link
{
    LinkNode *root;            // 根节点
    int length;                // 统计有多少数据
} LinkBST;                     // 别名

创建二叉搜索树，并初始化：

LinkBST bst;
bst.root = NULL;    // 根节点，初始化为NULL
bst.length = 0;     // 数据个数，初始化为0


创建节点（结构体数据类型），并创建具体节点实例的函数：

// 节点（结构体数据类型）
typedef struct Node
{
    int value;                // 数据类型为整型
    struct Node *left;        // 左子节点
    struct Node *right;       // 右子节点
} LinkNode;                   // 别名
// 函数：创建节点
LinkNode *createNode(int data)
{
    LinkNode *node = (LinkNode *)malloc(sizeof(LinkNode));    // 分配节点内存空间
    if(node == NULL)
    {
        perror("Memory allocation failed");
        exit(-1);
    }
    node->value = data;    // 数据
    node->left = NULL;     // 左子节点，初始化为NULL
    node->right = NULL;    // 右子节点，初始化为NULL
    return node;
}


添加元素：

从根节点开始，比对数值。若比它小，往左子树比对；若比它大，往右子树比对；直到找到为空，则为新元素的位置。

void add(LinkBST *bst, int data)	// add a element to the tree
{
	LinkNode *newNode = createNode(data);
	// 若是空树，根节点就是新节点
	if(bst->root == NULL)
	{
		bst->root = newNode;
		bst->length++;
		return ;
	}
	// 非空树，比根节点数值小，往左边比对，比根节点数值大，往右边比对
	LinkNode *cur = bst->root;
	while(1)
	{
		if(data == cur->value) return ;
		if(data < cur->value)
		{
			if(cur->left == NULL)
			{
				cur->left = newNode;
				bst->length++;
				return ;
			}
			cur = cur->left;
		}
		else if(data > cur->value)
		{
			if(cur->right == NULL)
			{
				cur->right = newNode;
				bst->length++;
				return ;
			}
			cur = cur->right;
		}
	}
}

删除元素：

  • 若删除的节点为叶子节点（即无子节点），则直接删除。
  • 若删除的节点只有左子节点，则左子节点替代删除节点。
  • 若删除的节点只有右子节点，则右子节点替代删除节点。
  • 若删除的节点既有左子节点又有右子节点，则找到直接前驱（即删除节点的左子树中的最大值，即删除节点的左子节点的最右节点），直接前驱的值替代删除节点的值，删除直接前驱节点。
void delete(LinkBST *bst,int data)	// delete a element from the tree
{
	// 函数：删除节点的具体操作
	LinkNode *del(LinkNode *node)
	{
		// 只有右子节点，右子节点替代删除节点
		if(node->left == NULL)
		{
			bst->length--;
			return node->right;
		}
		// 只有左子节点，左子节点替代删除节点
		if(node->right == NULL)
		{
			bst->length--;
			return node->left;
		}
		// 左右子节点都有，直接前驱(左子节点的最右节点,即左子树中最大值)替代删除节点,删除直接前驱
		if(node->left && node->right)
		{
			LinkNode *tmp = node, *cur = node->left;
			while(cur->right)
			{
				tmp = cur;
				cur = cur->right;
			}
			node->value = cur->value;
			bst->length--;
			if(tmp != node) tmp->right = cur->left;
			else tmp->left = cur->left;
			return node;
		}
	}
	
	// 函数：找到删除节点
	void delNode(int data)
	{
		LinkNode *parent, *cur = bst->root;
		while(1)
		{
			if(cur == NULL) return ;
			if(data == cur->value)
			{
				// 删除节点若是根节点，根节点接收删除后的节点
				if(cur == bst->root) bst->root = del(cur);
				// 删除节点若是左子节点，父节点的左子节点接收删除后的节点
				else if(data < parent->value) parent->left = del(cur);
				// 删除节点若是右子节点，父节点的右子节点接收删除后的节点
				else if(data > parent->value) parent->right = del(cur);
				return ;
			}
			if(data < cur->value)
			{
				parent = cur;
				cur = cur->left;
			}
			else if(data > cur->value)
			{
				parent = cur;
				cur = cur->right;
			}
		}
	}
    // 空树，直接退出程序
	if(bst->root == NULL) return ;
	delNode(data);
}

遍历元素：

前序遍历：（顺序：根节点、左子节点、右子节点）

使用数组实现栈（后进先出），数量：一个栈。

1、起始栈中元素为根节点。2、栈中元素依次出栈（并打印），找到元素的右节点和左节点依次入栈（注意：先右后左）。3、重复2，直到栈为空。

void pretraverse(LinkBST *bst)	// show element one by one,(root,left,right)
{
	LinkNode *cur = NULL;
	// 指针数组(数组元素是指针),实现栈(后进先出)
	LinkNode *arr[bst->length];
	int n = 1;
	arr[n-1] = bst->root;
	printf("pretravel: ");
	while(n != 0)
	{
		cur = arr[n-1];
		printf("%d  ", cur->value);
		n--;
		if(cur->right)
		{
			arr[n] = cur->right;
			n++;
		}
		if(cur->left)
		{
			arr[n] = cur->left;
			n++;
		}
	}
	printf("\n");
}

中序遍历：（顺序：左子节点、根节点、右子节点）

使用数组实现栈（后进先出），数量：一个栈。

1、从根节点开始遍历，根节点入栈。2、找左节点依次入栈，找到最左节点后，栈中元素依次出栈（并打印），找右节点入栈。3、重复2，直到节点不存在或者栈为空。

void midtraverse(LinkBST *bst)	// show element one by one,(left,root,right)
{
	printf("midtravel: ");
	LinkNode *cur = bst->root;
	// 指针数组(数组元素是指针),实现栈(后进先出)
	LinkNode *arr[bst->length];
	int n = 0;
	while(cur || n != 0)
	{
		if(cur)
		{
			arr[n] = cur;
			n++;
			cur = cur->left;
		}
		else
		{
			cur = arr[n-1];
			printf("%d  ", cur->value);
			n--;
			cur = cur->right;
		}
	}
	printf("\n");
}

后序遍历：（顺序：左子节点、右子节点、根节点）

使用数组实现栈（后进先出），数量：两个栈（辅助栈，目标栈）。

1、辅助栈中起始元素为根节点。2、辅助栈中元素依次出栈（并入栈目标栈），找到元素的左节点和右节点依次入栈辅助栈（注意：先左后右）。3、重复2，直到辅助栈为空。4、遍历目标栈，并打印。

void posttraverse(LinkBST *bst)	// show element one by one,(left,right,root)
{
	LinkNode *cur = NULL;
	// 指针数组(数组元素是指针),实现栈(后进先出)
	LinkNode *arr[bst->length];    // 辅助栈
	LinkNode *brr[bst->length];    // 目标栈
	int n = 1, m = 0;
	arr[n-1] = bst->root;
	while(n != 0)
	{	
		cur = brr[m] = arr[n-1];    // 辅助栈出栈，目标栈入栈
		n--;
		m++;
		if(cur->left)
		{
			arr[n] = cur->left;    // 辅助栈入栈
			n++;
		}
		if(cur->right)
		{
			arr[n] = cur->right;    // 辅助栈入栈
			n++;
		}
	}
    // 遍历目标栈
	printf("posttravel: ");
	for(int i = m - 1; i >= 0; i--)
	{
		printf("%d  ", brr[i]->value);
	}
	printf("\n");
}

广度遍历（层级遍历）：

使用链表实现队列（先进先出），数量：一个队列。

1、队列中起始元素为根节点。2、队列中元素依次从队头出队（并打印），找到元素的左节点和右节点依次从队尾入队（注意：先左后右）。3、重复2，直到队列为空。

void breadthtraverse(LinkBST *bst)	// show element one by one,(levels)
{
	printf("threadtravel: ");
	// 链表：实现队列(先进先出)，注：链表的函数在bstqueue.c(完整代码中展示)
	Queue queue;
	queue.header = createQnode(bst->root);    // 头指针，指向第一个元素
	queue.tail = NULL;                        // 尾指针，指向最后一个元素
	LinkNode *cur = NULL;
	while(queue.header)
	{
		cur = queue.header->bstnode;
		printf("%d  ", cur->value);
		popQnode(&queue);                    // 从队头出队(函数在bstqueue.c)
		if(cur->left)
		{
			addQnode(&queue, cur->left);    // 从队尾入队(函数在bstqueue.c)
		}
		if(cur->right)
		{
			addQnode(&queue, cur->right);    // 从队尾入队(函数在bstqueue.c)
		}
	}
	printf("\n");
}

查找元素：

从根节点开始，比对数值。若比它小，往左子树查找；若比它大，往右子树查找；直到找到该元素，则返回1（true），若没有，则返回0（false）。

int find(LinkNode *node, int data)	// if find data,return 1(true),or return 0(false)
{
	LinkNode *cur = node;
	while(cur)
	{
		if(data == cur->value) return 1;
		if(data < cur->value) cur = cur->left;
		else if(data > cur->value) cur = cur->right;
	}
	return 0;
}

完整代码：（bstree.c，bstqueue.c（链表实现的队列，用于广度遍历））

// bstree.c
#include <stdio.h>
#include <stdlib.h>
#include "bstqueue.c"    // 引入链表实现的队列，用于广度遍历

/* structure */
typedef struct Node		// node of the binary search tree(bst)
{
	int value;		    // data type is integer
	struct Node *left;	// left child node
	struct Node *right;	// right child node
} LinkNode;

typedef struct Link		//bst(Linkedlist)
{
	LinkNode *root;		// root node
	int length;		    // the number of the tree
} LinkBST;

/* function prototype */
void add(LinkBST *, int);	    // add a element
void delete(LinkBST *,int);	    // delete a element
void pretraverse(LinkBST *);	// show element one by one,(root,left,right)
void midtraverse(LinkBST *);	// show element one by one,(left,root,right)
void posttraverse(LinkBST *);	// show element one by one,(left,right,root)
void breadthtraverse(LinkBST *);	// show element one by one,(levels)
int find(LinkNode *, int);	    // if find data,return 1(true),or return 0(false)

/* main function */
int main(void)
{
	// create binary search tree and initialization
	LinkBST bst;
	bst.root = NULL;
	bst.length = 0;
	printf("isempty(1:true, 0:false): %d, length is %d\n", bst.root==NULL, bst.length);

	add(&bst, 15);
	add(&bst, 8);
	add(&bst, 23);
	add(&bst, 19);
	add(&bst, 10);
	add(&bst, 6);
	add(&bst, 9);
	add(&bst, 12);
	
	printf("isempty(1:true, 0:false): %d, length is %d\n", bst.root==NULL, bst.length);
	pretraverse(&bst);
	midtraverse(&bst);
	posttraverse(&bst);
	breadthtraverse(&bst);

	printf("find 10(1:true, 0:false): %d\n", find(bst.root, 10));
	printf("find 11(1:true, 0:false): %d\n", find(bst.root, 11));

	delete(&bst, 23);
	delete(&bst, 15);
	delete(&bst, 6);
		
	printf("isempty(1:true, 0:false): %d, length is %d\n", bst.root==NULL, bst.length);
	pretraverse(&bst);
	midtraverse(&bst);
	posttraverse(&bst);
	breadthtraverse(&bst);
	return 0;
}

/* subfunction */
LinkNode *createNode(int data)		// create a node of the binary search tree
{
	LinkNode *node = (LinkNode *)malloc(sizeof(LinkNode));
	if(node == NULL)
	{
		perror("Memory allocation failed");
		exit(-1);
	}
	node->value = data;
	node->left = NULL;
	node->right = NULL;
	return node;
}

void add(LinkBST *bst, int data)	// add a element to the tree
{
	LinkNode *newNode = createNode(data);
	// if empty, root is newNode
	if(bst->root == NULL)
	{
		bst->root = newNode;
		bst->length++;
		return ;
	}
	// if not empty, smaller,to left, biger,to right
	LinkNode *cur = bst->root;
	while(1)
	{
		if(data == cur->value) return ;
		if(data < cur->value)
		{
			if(cur->left == NULL)
			{
				cur->left = newNode;
				bst->length++;
				return ;
			}
			cur = cur->left;
		}
		else if(data > cur->value)
		{
			if(cur->right == NULL)
			{
				cur->right = newNode;
				bst->length++;
				return ;
			}
			cur = cur->right;
		}
	}
}

void delete(LinkBST *bst,int data)	// delete a element from the tree
{
	// subfunction: delete the node
	LinkNode *del(LinkNode *node)
	{
		// if only right child, return right child node
		if(node->left == NULL)
		{
			bst->length--;
			return node->right;
		}
		// if only left child, return left child node
		if(node->right == NULL)
		{
			bst->length--;
			return node->left;
		}
		// both left and right, the max on the left replace the delete node and delete it
		if(node->left && node->right)
		{
			LinkNode *tmp = node, *cur = node->left;
			while(cur->right)
			{
				tmp = cur;
				cur = cur->right;
			}
			node->value = cur->value;
			bst->length--;
			if(tmp != node) tmp->right = cur->left;
			else tmp->left = cur->left;
			return node;
		}
	}
	
	// subfunction: find the delete node
	void delNode(int data)
	{
		LinkNode *parent, *cur = bst->root;
		while(1)
		{
			if(cur == NULL) return ;
			if(data == cur->value)
			{
				// delete node is root,root receive the node after delete
				if(cur == bst->root) bst->root = del(cur);
				// delete node is left,left child of parent receive the node after delete
				else if(data < parent->value) parent->left = del(cur);
				//delete node is right,right child of parent receive the node after delete
				else if(data > parent->value) parent->right = del(cur);
				return ;
			}
			if(data < cur->value)
			{
				parent = cur;
				cur = cur->left;
			}
			else if(data > cur->value)
			{
				parent = cur;
				cur = cur->right;
			}
		}
	}

	if(bst->root == NULL) return ;
	delNode(data);
}

void pretraverse(LinkBST *bst)	// show element one by one,(root,left,right)
{
	LinkNode *cur = NULL;
	// pointer array(stack:LIFO): array, each element is a pointer(point to node)
	LinkNode *arr[bst->length];
	int n = 1;
	arr[n-1] = bst->root;
	printf("pretravel: ");
	while(n != 0)
	{
		cur = arr[n-1];
		printf("%d  ", cur->value);
		n--;
		if(cur->right)
		{
			arr[n] = cur->right;
			n++;
		}
		if(cur->left)
		{
			arr[n] = cur->left;
			n++;
		}
	}
	printf("\n");
}

void midtraverse(LinkBST *bst)	// show element one by one,(left,root,right)
{
	printf("midtravel: ");
	LinkNode *cur = bst->root;
	// pointer array(stack:LIFO): array, each element is a pointer(point to node)
	LinkNode *arr[bst->length];
	int n = 0;
	while(cur || n != 0)
	{
		if(cur)
		{
			arr[n] = cur;
			n++;
			cur = cur->left;
		}
		else
		{
			cur = arr[n-1];
			printf("%d  ", cur->value);
			n--;
			cur = cur->right;
		}
	}
	printf("\n");
}

void posttraverse(LinkBST *bst)	// show element one by one,(left,right,root)
{
	LinkNode *cur = NULL;
	// pointer array(stack:LIFO): array, each element is a pointer(point to node)
	LinkNode *arr[bst->length];
	LinkNode *brr[bst->length];
	int n = 1, m = 0;
	arr[n-1] = bst->root;
	while(n != 0)
	{	
		cur = brr[m] = arr[n-1];
		n--;
		m++;
		if(cur->left)
		{
			arr[n] = cur->left;
			n++;
		}
		if(cur->right)
		{
			arr[n] = cur->right;
			n++;
		}
	}
	printf("posttravel: ");
	for(int i = m - 1; i >= 0; i--)
	{
		printf("%d  ", brr[i]->value);
	}
	printf("\n");
}

void breadthtraverse(LinkBST *bst)	// show element one by one,(levels)
{
	printf("threadtravel: ");
	// queue(FIFO): use Linkedlist implement
	Queue queue;
	queue.header = createQnode(bst->root);
	queue.tail = NULL;
	LinkNode *cur = NULL;
	while(queue.header)
	{
		cur = queue.header->bstnode;
		printf("%d  ", cur->value);
		popQnode(&queue);
		if(cur->left)
		{
			addQnode(&queue, cur->left);
		}
		if(cur->right)
		{
			addQnode(&queue, cur->right);
		}
	}
	printf("\n");
}

int find(LinkNode *node, int data)	// if find data,return 1(true),or return 0(false)
{
	LinkNode *cur = node;
	while(cur)
	{
		if(data == cur->value) return 1;
		if(data < cur->value) cur = cur->left;
		else if(data > cur->value) cur = cur->right;
	}
	return 0;
}
// bstqueue.c
#include <stdlib.h>

/* structure */
typedef struct queueNode	// node of the queue
{
	void *bstnode;			// data type is bst node
	struct queueNode *next;	// point to next node
} Qnode;

typedef struct queue		// queue(Linkedlist)
{
	Qnode *header;		    // point to the top node
	Qnode *tail;		    // point to the last node
} Queue;

/* subfunction */
Qnode *createQnode(void *bstnode)	// create a node of the queue
{
	Qnode *node = (Qnode *)malloc(sizeof(Qnode));
	if(node == NULL)
	{
		perror("Memory allocation failed");
		exit(-1);
	}
	node->bstnode = bstnode;
	node->next = NULL;
	return node;
}

void addQnode(Queue *queue, void *node)	// add a element to the end of the queue
{
	Qnode *qnode = createQnode(node);
	if(queue->tail == NULL) queue->tail = queue->header = qnode;
	else
	{
		queue->tail->next = qnode;
		queue->tail = qnode;
	}
}

void popQnode(Queue *queue)		// delete a element from the top of the queue
{
	queue->header = queue->header->next;
	if(queue->header == NULL) queue->tail = NULL;
}

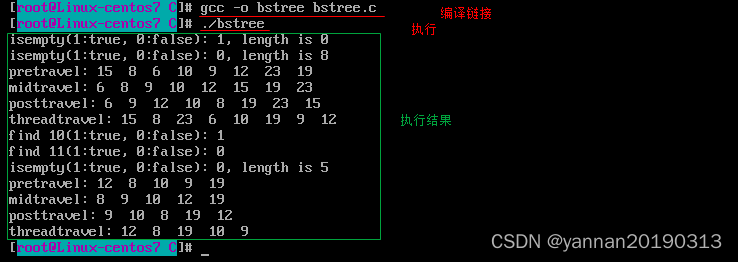
编译链接： gcc -o bstree bstree.c

执行可执行文件： ./bstree

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1906390.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

控件-ProgressBar

控件-ProgressBar

常用属性 1.android:max:进度条的最大值 2. android: progress:进度条已完成进度值 3. android: indeterminate:如果设置成true,则进度条不精确显示进度 4.style"?android:attr/progressBarStyleHorizontal"水平进度条 案例 进度条加载
阅读更多...
基于Java+SpringMvc+Vue技术的就医管理系统设计与实现系统(源码+LW+部署讲解)

基于Java+SpringMvc+Vue技术的就医管理系统设计与实现系统(源码+LW+部署讲解)

目录 界面展示 第六章 部分代码实现 6.1 Spring boot 配置代码 6.2 用户管理及登录登出代码 6.3 Md5 加密算法代码 6.4 部分数据库代码 六、论文参考&#xff1a; 七、其他案例&#xff1a; 系统介绍&#xff1a; 就医管理系统&#xff0c;也称为医院管理系统&#…
阅读更多...
STM32自己从零开始实操08:STM32主控原理图

STM32自己从零开始实操08:STM32主控原理图

由于老师使用的各引脚分门别类的单片机原理图我没有找到&#xff0c;我使用是引脚按顺序摆放的&#xff0c;不方便一个模块一个模块截图展示&#xff0c;所以这部分使用老师的原理图。 一、电源 1.1电源的介绍 1.1.1数字电源和地&#xff08;VDD和VSS&#xff09; 数字电源…
阅读更多...
AIGC时代程序员的跃迁——编程高手的密码武器

AIGC时代程序员的跃迁——编程高手的密码武器

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
RocketMQ之消费者带你了解概念和消费流程

RocketMQ之消费者带你了解概念和消费流程

1. 背景 RocketMQ 的消费可以算是 RocketMQ 的业务逻辑中最复杂的一块。这里面涉及到许多消费模式和特性。本想一篇文章写完&#xff0c;写到后面发现消费涉及到的内容太多&#xff0c;于是决定分多篇来写。本文作为消费系列的第一篇&#xff0c;主要讲述 RocketMQ 消费涉及到…
阅读更多...
网络规划与设计————期末复习

网络规划与设计————期末复习

一、选择题&#xff08;每题1分&#xff09; 1、光纤线组建的标准以太网是______。 A.10BASE-5 B.10BASE-2 C.10BASE-T D.10BASE-F 其实也很好记&#xff0c;光纤的英文是 "Fiber Optic"&#xff0c;双绞线的英文是 "Twisted Pair"。 5呢…
阅读更多...
Redis核心问题总结(一)

Redis核心问题总结(一)

1、为什么要使用Redis做缓存 缓存的好处 使用缓存的目的就是提升读写性能。而实际业务场景下&#xff0c;更多的是为了提升读性能&#xff0c;带来更好的性 能&#xff0c;带来更高的并发量。Redis 的读写性能比 Mysql 好的多&#xff0c;我们就可以把 Mysql 中的热点数据缓 …
阅读更多...
Python28-8 GBM梯度提升算法

Python28-8 GBM梯度提升算法

梯度提升算法&#xff08;Gradient Boosting Machine&#xff0c;GBM&#xff09;是一种集成学习方法&#xff0c;通过逐步构建一系列简单模型&#xff08;通常是决策树&#xff09;&#xff0c;并结合这些模型来提高整体预测性能。GBM广泛用于回归和分类任务&#xff0c;因为它…
阅读更多...
端到端自动驾驶新突破：Nvidia提出全并行PARA-Drive，斩获CVPR挑战赛冠军

端到端自动驾驶新突破：Nvidia提出全并行PARA-Drive，斩获CVPR挑战赛冠军

论文标题&#xff1a; PARA-Drive: Parallelized Architecture for Real-time Autonomous Driving 论文作者&#xff1a; Xinshuo Weng, Boris Ivanovic, Yan Wang, Yue Wang, Marco Pavone 导读&#xff1a; 本文系统分析了自动驾驶高级架构的设计空间&#xff0c;提出了关…
阅读更多...
单片机软件架构连载(3)-typedef

单片机软件架构连载(3)-typedef

今天给大家讲typedef&#xff0c;这个关键字在实际产品开发中&#xff0c;也是海量应用。 技术涉及知识点比较多&#xff0c;有些并不常用&#xff0c;我们以贴近实际为原则&#xff0c;让大家把学习时间都花在重点上。 1.typedef的概念 typedef 是 C 语言中的一个关键字&…
阅读更多...
artts升级版本后常见的编译错误（定期更新......）

artts升级版本后常见的编译错误（定期更新......）

1、设置泛型将参数配置为 null 时抛出了如下异常: Type null is not assignable to type T. T could be instantiated with an arbitrary type which could be unrelated to null. <ArkTSCheck> 解决办法 在 null 后面添加 ! 即可,以表示该值不会为 null data: T null!…
阅读更多...
【可能是全网最丝滑的LangChain教程】十七、LangChain进阶之Retrievers

【可能是全网最丝滑的LangChain教程】十七、LangChain进阶之Retrievers

人生不能像做菜&#xff0c;把所有的料都准备好了才下锅。 01 Retrievers介绍 检索器&#xff08;Retrievers&#xff09; 是一种接口&#xff0c;用于根据非结构化查询返回文档&#xff0c;它比向量存储更为通用&#xff0c;既可以使用向量存储作为底层&#xff0c;也可以是其…
阅读更多...
C++11右值引用及移动构造

C++11右值引用及移动构造

区分左值和右值 在学习c11的右值引用前&#xff0c;大家肯定会有点陌生什么是右值&#xff1f;什么是左值&#xff1f;现在我先来带大家熟悉一下概念。 左值 可以被取地址&#xff0c;也可被修改&#xff08;const修饰的除外&#xff09; 可以出现在等号左边&#xff0c;也可…
阅读更多...
华为HCIP Datacom H12-821 卷29

华为HCIP Datacom H12-821 卷29

1.多选题 下面关于LSA age字段&#xff0c;描述正确的是∶ A、LSA age的单位为秒&#xff0c;在LSDB中的LSA的LS age随时间增长而增长 B、LSA age的单位为秒&#xff0c;在LSDB中的LSA的LS age随时间增长而减少 C、如果一条LSA的LS age达到了LS RefreshTime&#xff08…
阅读更多...
【C++】AVL树（旋转、平衡因子）

【C++】AVL树（旋转、平衡因子）

&#x1f308;个人主页&#xff1a;秦jh_-CSDN博客&#x1f525; 系列专栏&#xff1a;https://blog.csdn.net/qinjh_/category_12575764.html?spm1001.2014.3001.5482 ​ 目录 前言 AVL树的概念 节点 插入 AVL树的旋转 新节点插入较高左子树的左侧---左左&#xff1a;…
阅读更多...
Spring的AOP基础以及AOP的核心概念

Spring的AOP基础以及AOP的核心概念

2. AOP基础 学习完spring的事务管理之后&#xff0c;接下来我们进入到AOP的学习。 AOP也是spring框架的第二大核心&#xff0c;我们先来学习AOP的基础。 在AOP基础这个阶段&#xff0c;我们首先介绍一下什么是AOP&#xff0c;再通过一个快速入门程序&#xff0c;让大家快速体…
阅读更多...
高级RAG检索中的五种查询重写策略_用于检索增强的大型语言模型的查询重写

高级RAG检索中的五种查询重写策略_用于检索增强的大型语言模型的查询重写

一、前言 检索增强生成 (RAG) 作为人工智能 (AI) 领域的一项重要技术&#xff0c;近年来得到了飞速发展。它将基于检索模型和基于生成的模型相结合&#xff0c;利用海量外部数据&#xff0c;生成更具信息量、更准确、更具语境相关性的回复。检索策略是 RAG 系统的关键组成部分…
阅读更多...
2024年最适合高级网工的11款Linux

2024年最适合高级网工的11款Linux

号主&#xff1a;老杨丨11年资深网络工程师&#xff0c;更多网工提升干货&#xff0c;请关注公众号&#xff1a;网络工程师俱乐部 你们好&#xff0c;我的网工朋友。 Linux作为一个免费且开源的操作系统&#xff0c;随着时间的推移催生了多个发行版&#xff0c;并且得到了庞大…
阅读更多...
golang验证Etherscan上的智能合约

golang验证Etherscan上的智能合约

文章目录 golang验证Etherscan上的智能合约为什么要验证智能合约如何使用golang去验证合约获取EtherscanAPI密钥Verify Source Code接口Check Source Code Verification Status接口演示示例及注意事项网络问题无法调用Etherscan接口&#xff08;最重要的步骤&#xff09; golan…
阅读更多...
应用层协议原理——因特网提供的运输服务

应用层协议原理——因特网提供的运输服务

我们已经考虑了计算机网络能够一般性地提供的运输服务。现在我们要更为具体地考察由因特网提供的运输服务类型。因特网(更一般的是TCP/IP网络)为应用程序提供两个运输层协议&#xff0c;即UDP和TCP。当软件开发者为因特网创建一个新的应用时&#xff0c;首先要做出的决定是&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023