梯度提升算法(Gradient Boosting Machine,GBM)是一种集成学习方法,通过逐步构建一系列简单模型(通常是决策树),并结合这些模型来提高整体预测性能。GBM广泛用于回归和分类任务,因为它具有较高的准确性和灵活性。
GBM的基本原理
GBM的思想源于提升方法(Boosting)。提升方法是一种将多个弱学习器(性能稍好于随机猜测的模型)组合成一个强学习器的技术。GBM通过以下步骤实现这一过程:
-
初始化模型:选择一个初始模型 ,通常是目标值的均值:
其中,是损失函数,是真实值。
-
迭代更新模型:对于每一轮 ,执行以下步骤:
-
计算残差:计算当前模型的预测误差(残差),即:
这里,残差表示真实值和当前模型预测值之间的差异。
-
拟合弱学习器:训练一个新的弱学习器 来拟合这些残差:
-
更新模型:更新模型的预测值,将新弱学习器加入现有模型中,并乘以一个学习率 来控制每个弱学习器的贡献:
其中,是学习率,通常介于 0 到 1 之间。
-
-
重复迭代:继续迭代步骤2,直到达到预定的迭代次数 或其他停止条件。
损失函数和梯度
GBM的核心在于利用损失函数的梯度来引导模型更新。不同的损失函数适用于不同的任务:
-
对于回归问题,常用的损失函数是均方误差(MSE):
-
对于分类问题,常用的损失函数是对数损失(Log Loss):
在每次迭代中,计算损失函数的负梯度作为残差,用于拟合新的弱学习器。
Python实例
以下是一个更详细的Python实例,展示如何使用GBM进行回归任务,并包含更多的解释和参数设置:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error
# 生成示例数据
np.random.seed(42) # 设置随机种子以保证结果可重复
X = np.random.rand(1000, 10) # 生成1000个样本,每个样本有10个特征的随机数据
y = X @ np.random.rand(10) + np.random.rand(1000) * 0.1 # 生成目标值y,是特征的线性组合加上噪声
# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 80%数据用于训练,20%数据用于测试
# 创建梯度提升回归器
gbm = GradientBoostingRegressor(n_estimators=200, learning_rate=0.1, max_depth=3, random_state=42) # 创建GBM回归器,设置树的数量、学习率和最大深度
# 训练模型
gbm.fit(X_train, y_train) # 在训练集上训练GBM模型
# 初始化列表存储训练误差和测试误差
train_errors = []
test_errors = []
# 使用staged_predict获取每个阶段的预测误差
for y_train_pred in gbm.staged_predict(X_train):
train_errors.append(mean_squared_error(y_train, y_train_pred)) # 记录训练误差
for y_test_pred in gbm.staged_predict(X_test):
test_errors.append(mean_squared_error(y_test, y_test_pred)) # 记录测试误差
# 绘制训练过程中树的数量与均方误差的关系
plt.figure(figsize=(12, 6)) # 设置图形大小
plt.plot(range(1, gbm.n_estimators + 1), train_errors, label='Train') # 绘制训练误差曲线
plt.plot(range(1, gbm.n_estimators + 1), test_errors, label='Test') # 绘制测试误差曲线
plt.xlabel('Number of Trees') # 设置x轴标签
plt.ylabel('Mean Squared Error') # 设置y轴标签
plt.title('Number of Trees vs. Mean Squared Error') # 设置图形标题
plt.legend() # 显示图例
plt.show() # 显示图形
# 显示特征重要性
feature_importance = pd.Series(gbm.feature_importances_, index=[f'Feature {i}' for i in range(X.shape[1])]) # 获取特征重要性
feature_importance.sort_values(ascending=False).plot(kind='bar', title='Feature Importance') # 绘制特征重要性条形图
plt.xlabel('Features') # 设置x轴标签
plt.ylabel('Importance') # 设置y轴标签
plt.show() # 显示图形
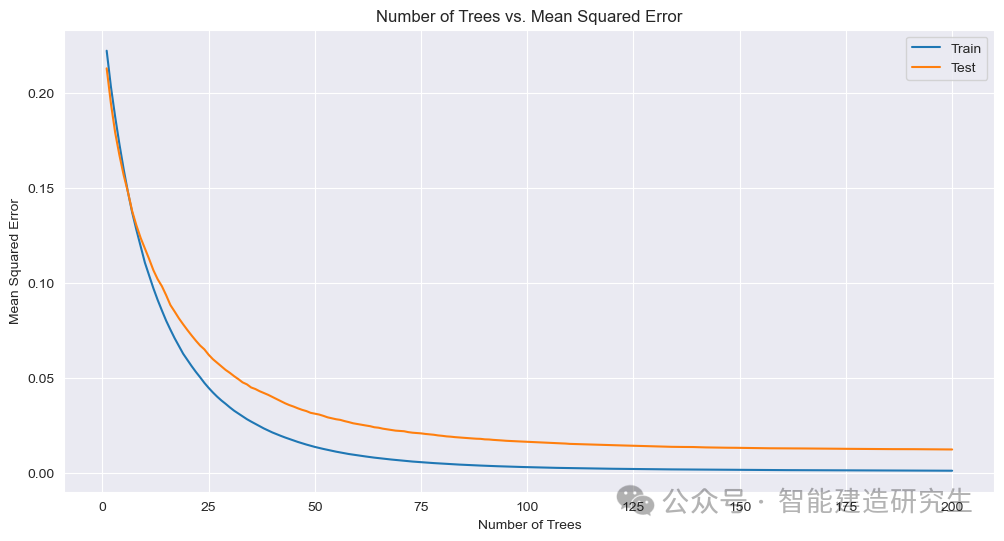
上图展示了模型在训练和测试集上的均方误差(MSE)随决策树数量增加的变化情况。可以看出随着决策树数量的增加,模型在训练集和测试集上的均方误差逐渐降低,逐渐趋近于0,表示模型的性能越来越好。
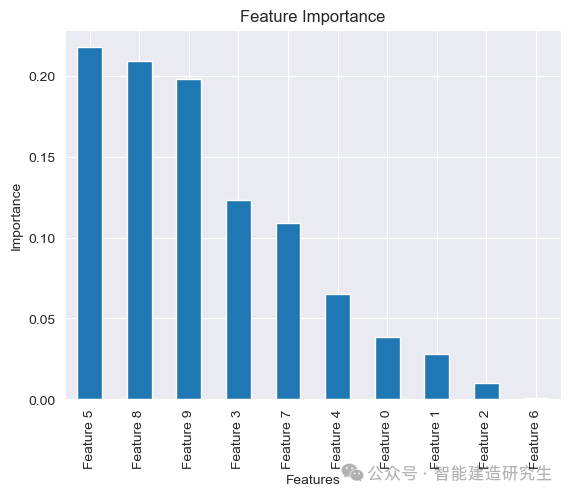
这张图展示了每个特征对模型的重要性排序,我们可以直观地看出特征5、8、9是重要性较高的前几个特征。
关键参数解释
-
n_estimators: 弱学习器的个数(即迭代次数)。更多的树可能会提升模型的准确性,但也会增加训练时间和可能的过拟合。 -
learning_rate: 学习率,用于缩小每个弱学习器的贡献。较小的学习率通常需要更多的树来达到同样的训练效果。 -
max_depth: 决策树的最大深度,控制每个弱学习器的复杂度。较浅的树可以防止过拟合。
优缺点
优点:
-
能够处理各种类型的数据,包括连续和离散数据。
-
具有较高的预测准确性,尤其在处理复杂数据集时表现优异。
-
具有特征选择的功能,可以输出特征的重要性。
缺点:
-
训练时间较长,尤其在数据集较大或参数设置较高时。
-
对于超参数(如树的数量、深度、学习率等)的选择较为敏感,需要进行调参以获得最佳性能。
梯度提升算法通过逐步构建和组合多个弱学习器,逐渐提升模型性能,是一种强大的机器学习方法。其灵活性和高准确性使其在许多实际应用中得到广泛使用。
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!