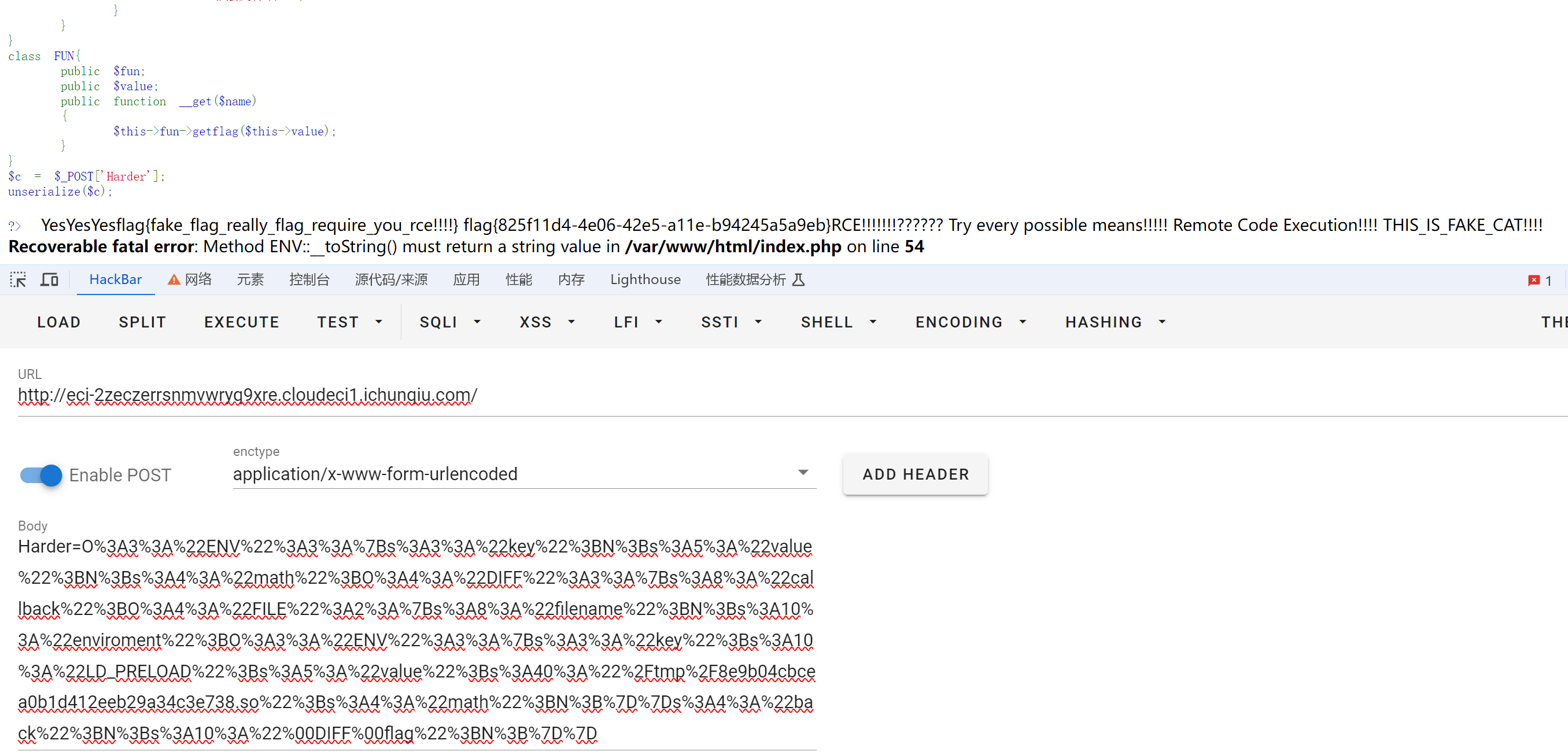
浮点数组成

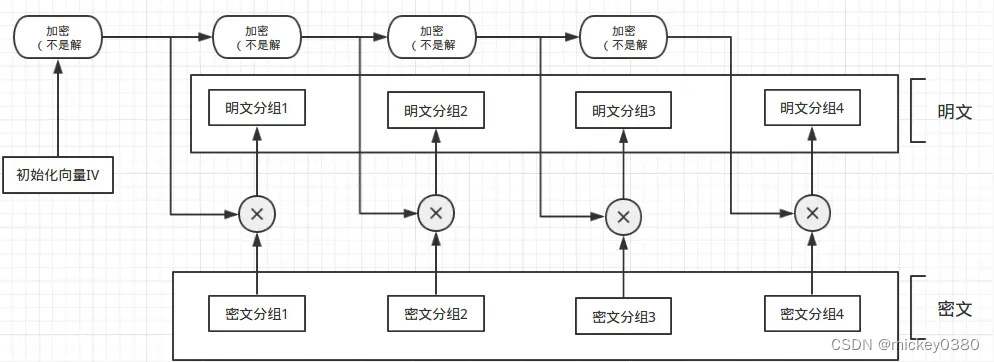
在计算机中浮点数通常由三部分组成：符号位、指数位、尾数位。IEEE-754中32位浮点数如下：

上图32bit浮点数包含1bit的符号位，8比特的指数位和23bit的尾数位。对于一个常规浮点数，我们来看看它是如何存储和计算的。这里以浮点数25.125为例。这个浮点数分为整数（25(d)）和小数部分（0.125(d)），（下面25(d)中d表示十进制，后续b表示二进制）
于是：
$$\begin{array}{rl}25(d)& =11001(b)\\ 0.125(d)& =0.001(b)\\ 25.125(d)& =11001.001(b)=1.1001001E^4(b)\end{array}$$
明显这个数是一个正数，所以我们可以得知符号位S=0。指数位的计算和我们想象的稍微有点区别，这里我们的2禁止指数位是4。在十几种考虑的指数位可能是负数，为了避免负数情况，我们可以将指数表达范围移动一个偏置到正数区域。因为我们的指数位位8bit，有符号整数最高能表示$2^7-1=127$，所以对指数位偏移一个127即可得到正数。所以我们的指数位部分为：$4(d)+127(d)=131(d)=10000011(b)$。接下来是尾数，因为$25.125(d)=11001.001(b)可以为1.1001001E^4(b)也可以为.11001001E^5(b)$这样我们就得到了不同的表示方法。为了确保总是用相同的方法表示浮点数，IEEE-754中要求了表示尾数的部分总是为1.xxx。正因如此，我们这里的指数部分才是4而不是5。也正是因为如此，所以我们只需要保存.xxx即可，因为小数点前一定是1，这样能节省一个bit。尾数部分为1001001，这样我们的浮点数在内存中表示为：01000001110010010000000000000000。这个值如果是32有符号的定点数int32他应该表示的为：1103691776。
0 10000011 10010010000000000000000

代码验证

#include <cstdint>
#include <iomanip>
#include <iostream>
#include <limits>

using namespace std;
// 定义一个联合体用于访问浮点数的内存表示
union FloatBits {
    float f;
    uint32_t bits;
};

// 打印浮点数的二进制表示
void printFloatBits(float value) {
    FloatBits fb;
    fb.f = value;

    std::cout << "Float value: " << std::fixed << std::setprecision(6) << value
              << std::endl;
    std::cout << "Binary representation: ";

    // 从最高位开始逐位打印
    for (int i = 31; i >= 0; --i) {
        // 通过位掩码检查每一位的值
        uint32_t mask = 1 << i;
        std::cout << ((fb.bits & mask) ? '1' : '0');

        // 在输出中添加空格分组
        if (i % 8 == 0)
            std::cout << ' ';
    }

    std::cout << std::endl;
}

int main() {
    float number = 25.125f;
    int a = 1103691776;
    float *b = reinterpret_cast<float *>(&a);
    int zp = 0;            // 00000000000000000000000000000000
    int zn = -2147483648;  // 10000000000000000000000000000000
    int infn = -8388608;   // 11111111100000000000000000000000
    int infp = 2139095040; // 01111111100000000000000000000000
    int nan = 2139095041;  // 01111111100000000000000000000001
    float inf_float = -std::numeric_limits<float>::infinity();
    std::cout << "-inf float for int  " << *reinterpret_cast<int *>(&inf_float)
              << " -inf float = " << inf_float << "\n";
    float *zero_pos = reinterpret_cast<float *>(&zp);
    float *zero_neg = reinterpret_cast<float *>(&zn);

    float *infn_f = reinterpret_cast<float *>(&infn);
    float *infp_f = reinterpret_cast<float *>(&infp);
    float *nan_f = reinterpret_cast<float *>(&nan);

    printFloatBits(number);
    std::cout << "a = " << a << " *b = " << *b << " number = " << number
              << " +0 => " << *zero_pos << " -0 =>" << *zero_neg << " +inf => "
              << *infp_f << " -inf => " << *infn_f << " nan => " << *nan_f
              << "\n";

    return 0;
}

使用GDB验证存储变量：

x/4tb:

• 4 :表示4个后面的元素
• t:表示打印为二进制
• b:打印单位为byte（8bit）。

你可能会感到疑惑为什么这个值看起来和我们的结果不太一样，这是因为我们的机器使用小端存储法。show endian可以打印当前运行机器上是大端存储还是小端存储法。实际的二进制按照高位字节存储在低位的方式存储。所以这个值作为二进制，我们应该反向理解为：0100000 111001001 00000000 00000000。同理你可以试一试打印变量a，你就会发现两着结果完全相同。尽管二进制上完全相同，但是因为用了不同的类型符修饰运算的时候依然能知道这个数是表示浮点数的25.125还是无符号整数的1103691776。

浮点数的特殊值

1. E不全为0或不全为1。这时，浮点数就采用偏置表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。
2. E全为0。这时，浮点数的指数E等于1-127（或者1-1023（64bit）），有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
3. E全为1。这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）（111111111000000000000000000000000(b)）

如何计算负数的二进制

1. 找到对应的正数（8388608），计算二进制（00000000100000000000000000000000）。
2. 反转所有位，得到二进制的反码(11111111011111111111111111111111)。
3. 反码+1得到二进制的补码(111111111000000000000000000000000)。