何为双指针
双指针指向同一数组,然后配合着进行搜索等活动。
滑动窗口的时候很好使用。
167.两数之和Ⅱ-输入有序数组
167. 两数之和 II - 输入有序数组
题目
给你一个下标从 1 开始的整数数组
numbers,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数target的两个数。如果设这两个数分别是numbers[index1]和numbers[index2],则1 <= index1 < index2 <= numbers.length。以长度为 2 的整数数组
[index1, index2]的形式返回这两个整数的下标index1和index2。你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。示例 2:
输入:numbers = [2,3,4], target = 6 输出:[1,3] 解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。示例 3:
输入:numbers = [-1,0], target = -1 输出:[1,2] 解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。提示:
2 <= numbers.length <= 3 *-1000 <= numbers[i] <= 1000numbers按 非递减顺序 排列-1000 <= target <= 1000- 仅存在一个有效答案
题解
判断两数之和是否等于target值。可以使用遍历。一般做法是通过确定第一个数,然后进行后续的遍历。但是这里有一个前提调节,numbers是有序数组。因此这里可以考虑使用双指针来解决问题。
让一个指针指向开头,一个指向结尾。如果相加比target小,那么指向开头的指针往后移,如果比target大,那就指向结尾的指针往前移。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int n=numbers.size();
int start=0,end=n-1;
int i;
while(numbers[start]+numbers[end]!=target){
if(numbers[start]+numbers[end]>target)
end--;
else
start++;
}
return vector<int>{start+1,end+1};
}
};88.合并两个有序数组
88. 合并两个有序数组
题目
给你两个按 非递减顺序 排列的整数数组
nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中,使合并后的数组同样按 非递减顺序 排列。注意:最终,合并后数组不应由函数返回,而是存储在数组
nums1中。为了应对这种情况,nums1的初始长度为m + n,其中前m个元素表示应合并的元素,后n个元素为0,应忽略。nums2的长度为n。示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200<= nums1[i], nums2[j] <=
题解
合并两个有序数组,且合并的时候不新建一个新的数组,直接修改nums1数组。因为nums1数组本身空间就是m+n,这个时候后面的n为0.
因此我们可以从nums1和nums2中非零的位置开始,置为指针。
比较越大的放在越后面,所以这里还需要一个pos指向nums1的最后。
这样子就可以实现数组的合并。
在这里需要注意一个点,当m或者n已经为0时,就不需要比较了。因为nums1本来就在nums1上,因此不需要继续赋值。如果n>0,那么就把nums2中的数复制过去。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int pos=m+n-1;
m=m-1;
n=n-1;
while(m>=0&&n>=0){
if(nums1[m]>nums2[n])
nums1[pos--]=nums1[m--];
else
nums1[pos--]=nums2[n--];
}
while(n>=0&&pos>=0){
nums1[pos--]=nums2[n--];
}
}
};142.环形链表Ⅱ
142. 环形链表 II
题目
给定一个链表的头节点
head,返回链表开始入环的第一个节点。 如果链表无环,则返回null。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。如果pos是-1,则在该链表中没有环。注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。不允许修改 链表。
示例 1:
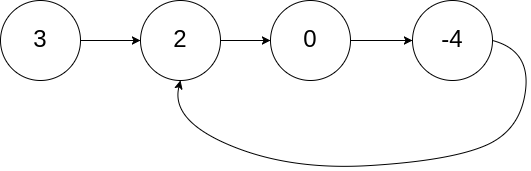
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
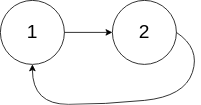
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。提示:
- 链表中节点的数目范围在范围
[0, 104]内<= Node.val <=
pos的值为-1或者链表中的一个有效索引
题解
补充一个知识
快慢指针(Floyd 判圈法)
对于链表找环路的问题,有一个通用的解法——快慢指(Floyd 判圈法)。给定两个指针,分别命名为slow 和fast,起始位置在链表的开头。每次fast 前进两步,slow 前进一步。如果fast可以走到尽头,那么说明没有环路;如果fast 可以无限走下去,那么说明一定有环路,且一定存在一个时刻slow 和fast 相遇。
当slow 和fast 第一次相遇时,我们将fast 重新移动到链表开头,并让slow 和fast 每次都前进一步。当slow 和fast 第二次相遇时,相遇的节点即为环路的开始点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast=head,*slow=head;
do{
if(fast==NULL||fast->next==NULL)
return NULL;
fast=fast->next->next;
slow=slow->next;
}while(fast!=slow);
fast=head;
while(fast!=slow){
fast=fast->next;
slow=slow->next;
}
return fast;
}
};76.最小覆盖子串
76. 最小覆盖子串
题目
给你一个字符串
s、一个字符串t。返回s中涵盖t所有字符的最小子串。如果s中不存在涵盖t所有字符的子串,则返回空字符串""。注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。- 如果
s中存在这样的子串,我们保证它是唯一的答案。示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。示例 2:
输入:s = "a", t = "a" 输出:"a" 解释:整个字符串 s 是最小覆盖子串。示例 3:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。提示:
m == s.lengthn == t.length1 <= m, n <=s和t由英文字母组成
题解
求S的最小子串,该子串只需要含有T中的字母就可以,不需要按顺序。
在这里我们首先可以申请两个标记数组,用来获取字符串t的字符和个数。
vector<int> words(128,0); vector<bool> flag(128,false); int i=0; for(i=0;i<t.size();i++){ words[t[i]]++; flag[t[i]]=true; }接着定义几个变量,一个是左右指针,还有一个是最小的长度以及最小字符串开始的位置。
首先是左指针不动,指向第一个位置。接着,右指针遍历,并且判断该字符是否是t中有的,如果有,个数减一,count++。直到count跟t一样长。这个时候我们就找到了一个字符串,包含t。但是不一定是最短的。这个时候我们就开始移动左指针。在移动的时候要判断,如果第一个位置是t中的,那么也要同步发生变化。
class Solution { public: string minWindow(string s, string t) { vector<int> words(128,0); vector<bool> flag(128,false); int i=0; for(i=0;i<t.size();i++){ words[t[i]]++; flag[t[i]]=true; } int l=0,r=0; int min_size=s.size()+1; int min_l=0,count=0; for(r=0;r<s.size();r++){ if(flag[s[r]]==true){ if(--words[s[r]]>=0){ count++; } while(count==t.size()){ if(r-l+1<min_size){ min_l=l; min_size=r-l+1; } if(flag[s[l]]==true&&++words[s[l]]>0){ count--; } l++; } } } return min_size>s.size()?"":s.substr(min_l,min_size); } };