【python中级】图像从从笛卡尔坐标系转换为极坐标系
- 1.背景
- 2.生成二维图
- 3.极坐标转换
1.背景
笛卡尔坐标系就是我们常说的直角坐标系。
笛卡尔坐标系,也称为直角坐标系,是由法国数学家和哲学家勒内·笛卡尔(René Descartes)发明的一种二维或三维坐标系统。它使用两个或三个相互垂直的轴来定义平面或空间中的点的位置。
二维笛卡尔坐标系 使用 x 轴和y 轴。这两个轴相互垂直,交于原点 (0,0)。
三维笛卡尔坐标系 使用x 轴、y 轴和 z 轴。这三个轴相互垂直,交于原点 (0,0,0)。
从笛卡尔坐标系转换为极坐标系的方法有线性和对数极坐标变换。
它们之间的主要区别在于径向距离 r 的计算方式。
1.1 线性极坐标变换 (Linear Polar Transformation)
在线性极坐标变换中,径向距离 r 直接与笛卡尔坐标系中的距离成正比:
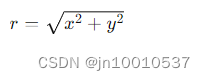
这种变换保持了距离的线性关系,也就是说,离原点越远的点在极坐标系中的径向距离越大。
线性极坐标变换适用于需要保持图像原始比例的情况。
1.2 对数极坐标变换 (Logarithmic Polar Transformation)
在对数极坐标变换中,径向距离 r 是对笛卡尔坐标系中的距离取对数的结果:(这里log即 lg:10为底的对数,叫作常用对数。)
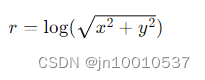 <
<