目录
顺序表的顺序存储结构
1.数组
2.顺序表
顺序表的声明，存储操作以及效率分析
1.泛型类
2.顺序表的插入操作
3. 顺序表的删除操作
4.顺序表查询操作
5.顺序表的应用
线性表的链式存储结构
单链表的基本操作
顺序表的顺序存储结构
数组是实现顺序存储结构的基础
1.数组
程序设计语言中，数组（Array）具有相同数据类型，是一个构造数据类型。
一维数组占用一块内存空间，每个存储单元的地址是连续的，数据的存储单位个数称为数组容量。设数组变量为a，第i个元素（存储单元）为a[i],其中序号i称为下标，一维数组使用一个下标唯一确定一个元素。
如果数据存储结构存取任何一个元素的时间复杂度是O(1)，则称其为随机存储结构。因此，数组是随机存储结构。
数组一旦占用一片存储空间，其地址和容量就是确定的，不能更改。因此，数组只能进行赋值，取值两种操作，不能进行插入和删除操作。当数组容量不够时，不能就地扩容。
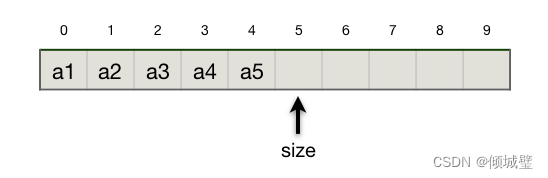
2.顺序表
线性表的顺序存储结构称为顺序表，它使用一维数组一次存放线性表的数据，且顺序表的性质和数组是一样的，因为顺序表的底层就是用数组来实现的。
顺序表的表现特点：
- 随机访问，可以在O(1)时间内找到第i个元素
- 存储密度高，每个节点只存储数据元素
- 扩展容量不方便（即便采用动态分配的方式实现，扩展长度的时间复杂度也比较高）
- 插入和删除操作不方便，需要移动大量元素
顺序表的声明，存储操作以及效率分析
1.泛型类
声明SeqList<T>为泛型类，类型形式参数称为泛型，T表示顺序表数据元素的数据类型。
JAVA语言约定。泛型<T>的实际参数必须是类，不能是int，char等基本数据类型。如果需要表示基本数据类型，也必须采用基本数据类型的包装类，如Integer，Character等等。
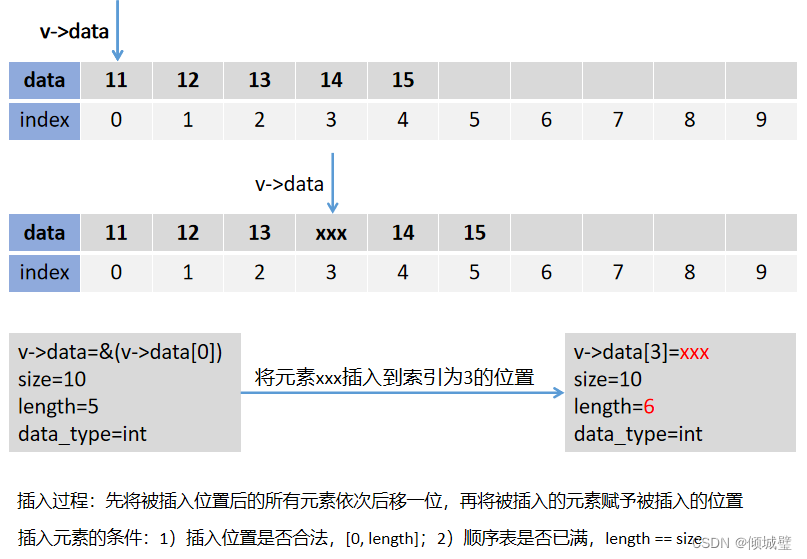
2.顺序表的插入操作
public class SequentialList{
private int[] array;//用于顺序表的数组
private int size;//顺序表的实际长度
public SequentialList(int capacity){
array =new int[capacity];
size=0;
}
//插入操作
public boolean insert(int index,int element){
//检查索引是否合法
if (index<0||index>size){
System.out.println("插入的位置不合法");
return false;
}
//如果数组已满，则无法插入
if (size==array.length){
System.out.println("顺序表已满，无法插入");
return false;
}
//从插入位置开始，所有的元素向后移动一位
for (int i =size;i>index;i--){
array[i]=array[i-1];
}
//插入元素
array[index]=element;
//更新顺序表的长度
size++;
return true;
}
public void printList(){
for (int i = 0; i < size; i++) {
System.out.println(array[i]+" ");
}
System.out.println();
}
public static void main(String[] args) {
SequentialList list =new SequentialList(10);
list.insert(0, 3); // 在索引0处插入元素3
list.insert(1, 7); // 在索引1处插入元素7
list.insert(2, 1); // 在索引2处插入元素1
list.insert(3, 4); // 在索引3处插入元素4
list.printList(); // 打印顺序表
}
}3. 顺序表的删除操作
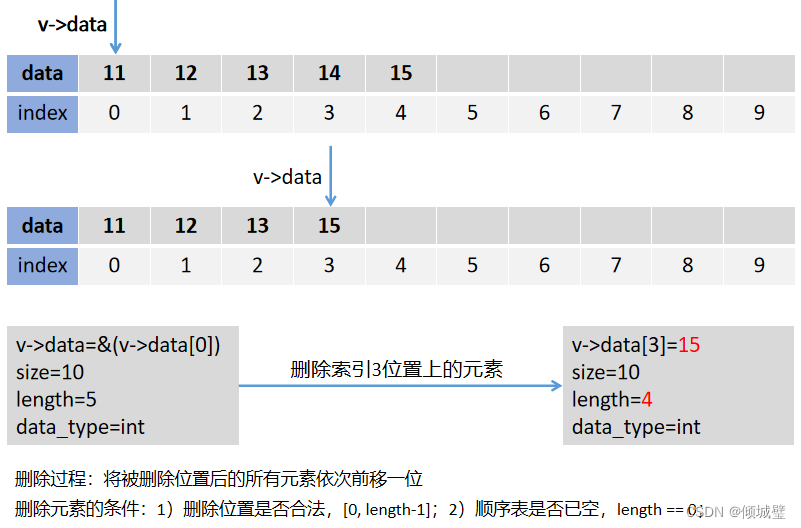对顺序表进行插入和删除操作时，算法所花费的时间主要用于移动元素。若插入或删除在最前面，则需要移动n个元素；若插入或删除元素在最后，则移动元素为0。设插入x作为第i个元素的概率为p，插入一个元素的平均移动到次数为O（n）。
4.顺序表查询操作
根据查找条件，对顺序表进行查找操作，采用顺序查找算法，在查找过程中，需要将key与顺序表顺序表元素逐个比较是否相等。而比较对象对象相等规则有原数所属的T类的equals（Object）方法实现。
public int search(T key){
for(int i =0;i<this.n;i++){
if (key.equals(this.element[i])){
return i;
}
}
return -1;
}顺序查找的比较次数取决于元素位置。时间复杂度也为O（n）。
静态顺序表的特性：
1. 固定大小：静态顺序表在创建时分配固定数量的内存空间，这个大小在定义后不能改变。
2. 内存分配：内存在编译时分配，因此内存使用是静态的，不会随程序运行而改变。
3. 空间浪费：如果实际存储的元素少于分配的空间，会造成内存浪费。
4. 无需移动元素：插入和删除操作不需要移动大量元素，因为有足够的空间来容纳新元素或释放空间。
5. 简单实现：由于内存空间固定，实现起来相对简单。
顺序表利用元素的物理存储次序反映线性表元素的逻辑次序，不需要额外空间来表达元素之间的关系。
插入和删除操作效率都很低。每插入或删除一个元素，元素移动量大，平均移动顺序表一半的元素。
顺序表（也称为数组）支持通过索引直接访问元素，这种情况下查找的时间复杂度是 O(1)。这意味着无论数组有多大，访问任何元素的时间都是恒定的，因为数组元素在内存中是连续存储的，可以通过简单的地址计算直接定位到元素。
如果你不知道元素的索引，而需要通过元素的值来查找它的位置，那么通常需要进行线性查找，这两种情况的时间复杂度为 O(n) 。
5.顺序表的应用
求解Josephus环的问题。
Josephus问题是一个著名的数学问题，以公元1世纪的犹太历史学家约瑟夫斯（Flavius Josephus）的名字命名。据说，在罗马占领期间，约瑟夫斯和他的39个同胞犹太士兵被罗马军队包围在一座山洞中，他们决定宁死不屈，并通过抽签决定自杀的顺序，每杀一个人，就按事先规定的顺序数到下一人，直到所有人都死去。约瑟夫斯和另外一个人是最后两个幸存者，他们决定不自杀，而是向罗马军队投降。
这个问题可以形式化为：n个人围成一圈，从第一个人开始，每数到第m个人，就将其处决，然后从下一个人重新开始数。这个过程一直进行，直到所有人都被处决。问题是，给定n和m，如何找到最后被处决的人的初始位置？
import java.util.ArrayList;
public class Josephus {
//n个人，n>0;从start开始技术，0<=start<n,每次数到distance的人出环，0<distance<n
public Josephus(int n ,int start,int distance){
if (n<=0||start<0||start>=n||distance<=0||distance>=n)
throw new IllegalArgumentException("n="+n+",start="+start+",distance="+distance+"");
//创建顺序表实例，元素类型是字符串，构造方法参数指定顺序表容量，省略时取默认值
ArrayList<String> list =new ArrayList<>();
for (int i =0;i<n;i++){
list.add((char)('A'+i)+"");
}
System.out.println(list.toString());
while(n>1){//循环，每次计算删除一个元素
start =(start+distance-1)%n;
//输出删除的start位置对象和顺序表中的剩余元素，两者均为Ｏ（ｎ）
System.out.println("删除"+list.remove(start).toString()+","+list.toString());
n--;
}
System.out.println("被赦免的人是"+list.get(0));
}
public static void main(String[] args) {
new Josephus(5,1,3);
}
}
运行结果：
[A, B, C, D, E]
删除D,[A, B, C, E]
删除B,[A, C, E]
删除A,[C, E]
删除C,[E]
E线性表的链式存储结构
线性表采用的是链式存储结构，别名单链表，用于储存逻辑关系为“一对一”的数据。与顺序表不同，链表不限制数据的物理存储状态，换句话说，使用链表存储的数据结构，其物理存储位置是随机的，因此必须采用指针变量记载前驱或后续元素的存储地址，存储数据元素之间的线性关系。
物理存储结构：在物理层面上，单链表的节点不需要在内存中连续存储。每个节点可以独立地存储在内存的任何位置，通过指针指向下一个节点，从而在逻辑上形成一个线性序列。这意味着，尽管节点在内存中是分散的，但它们通过指针连接起来，形成了一个完整的链表。
例如：
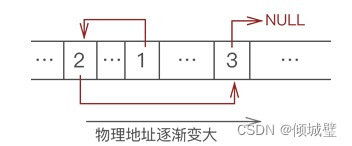
存储一个数据元素的存储单元称为节点（node）。结点结构如下，至少包含两个部分。
结点（数据域，地址域） //数据域存储数据元素，地址域（也称为链）存储前驱或后续元素地址每个结点只有一个地址域的线性链表称为单链表，空链表的头指针head为null；一个单链表最后一个节点的地址域为null
一个完整的链表需要由以下几个部分组成：
1.头指针：一个普通的指针，它的特点是永远指向链表第一个结点的位置。很明显，头指针用于指明链表的位置，便于后期找到链表并使用表中的数据。
2.节点：链表中的节点细分为头节点，首元节和其他节点
A.头节点：其实就是一个不存任何数据的空节点，通常作为链表的第一个节点，对于链表来说，头节点不是必须的，它的作用只是方便解决某些实际问题
B.首元节点：只是堆链表的第一个存有数据节点的一个称谓，没有实际含义。
C.其他节点：链表中其他的节点
单链表的基本操作
1.单链表的插入操作
在单链表中插入一个节点，根据不同的插入位置，分一下几种情况
- 在头节点前插入
- 在尾部插入
- 在某个特定的位置插入
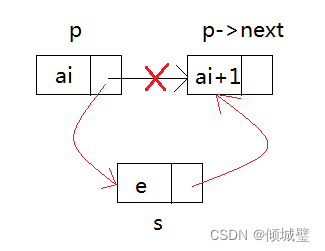
过程分析：
单链表第 i 个数据插入结点的算法思路：
1）声明一指针 p 指向链表头结点，初始化 j 从1开始
2）当 j<i 时，就遍历链表，让 p 的指针向后移动，不断指向下一结点，j 累加 1
3）若到链表末尾为空，则说明第 i 个结点不存在
4）否则查找成功，在系统中生成一个空节点s
5）将数据元素 e 赋值给 s->data
6）单链表的插入标准语句 s->next=p->next; p->next=s;
7）返回成功
public class test3 {
private Node head;//头节点
//节点内部类
private class Node{
int data;
Node next;
Node(int data){
this.data =data;
this.next=null;
}
}
//在链表的头部插入新的节点
public void insertAtHead(int data){
Node newNode =new Node(data);//创建一个新的节点newNode
newNode.next=head;//建立的新的节点Node指向head节点的链，即插入newNode节点在head节点的前
head=newNode;//使head指向newNode节点，则p节点成为第0个节点
}
//到链表的尾部插入新的节点
public void insertAtTail(int data){
Node newNode=new Node(data);//创建一个新的节点
if(head==null){//检查头节点是否为空
head=newNode;//如果链表为空，这行代码讲新节点赋值给头节点head
}else{
Node current =head;//这个用来辅助遍历链表
while(current.next!=null){//直到current指向链表的最后一个节点
current=current.next;//不断指向链表中下一个节点
}
current.next=newNode;//当循环结束时，newNode连接到链表的结尾
}
}
//在指定的位置插入新的节点
public void insertAtPosition(int position,int data){
if (position==0){
insertAtHead(data);
return;
}
Node newNode =new Node(data);
Node current=head;
for (int i =0;i<position-1&¤t!=null;i++){
current=current.next;
}
if (current==null){//如果current为null，说明指定的插入位置超出了链表当前长度
System.out.println("position"+position+"is out of bounds");
return;
}
newNode.next =current.next;
current.next=newNode;
}
}
疑问：为什么在单链表数据读取的时候，声明的指针p指向链表的第一个节点，而在单链表插入的时候，声明的指针p指向链表第一个节点，而在单链表插入时候，声明的指针p指向链表的头节点。
分析：
- 单链表读取的时候，是从头开始查找的，如果找到直接读取数据返回，显然这个跟头节点没什么关系，直接从第一个节点开始即可。
- 单链表插入的时候，查找到节点的情况下，是需要将p的后续节点改成s的后续节点，再将节点s变成p的后续节点。声明p指针指向链表头节点，p的后续节点就是第一节点，p的后续节点就是第一节点，就相当于从第一节点前插入，这显然符合要求。
- 如果声明的指针p指向第一个节点，那通过这个插入语句后，就相当于插入了第二个节点前，显然不符合要求。
2.删除单链表
删除单链表中的指定节点，通过改变节点的next域，就可以改变节点之间的连接关系，不需要移动元素。
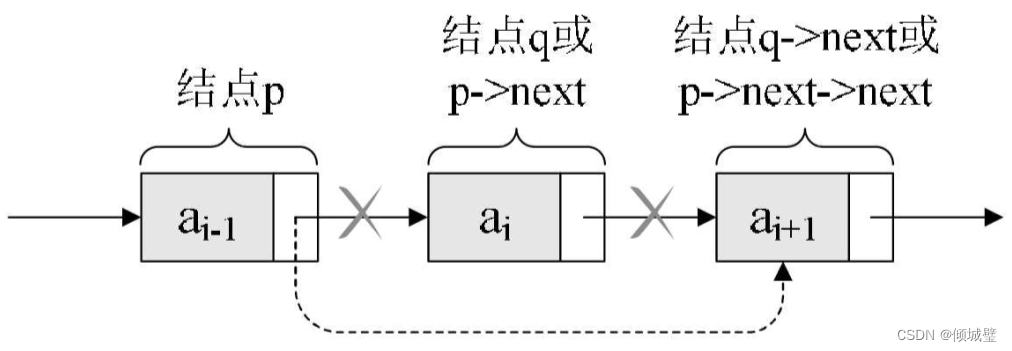
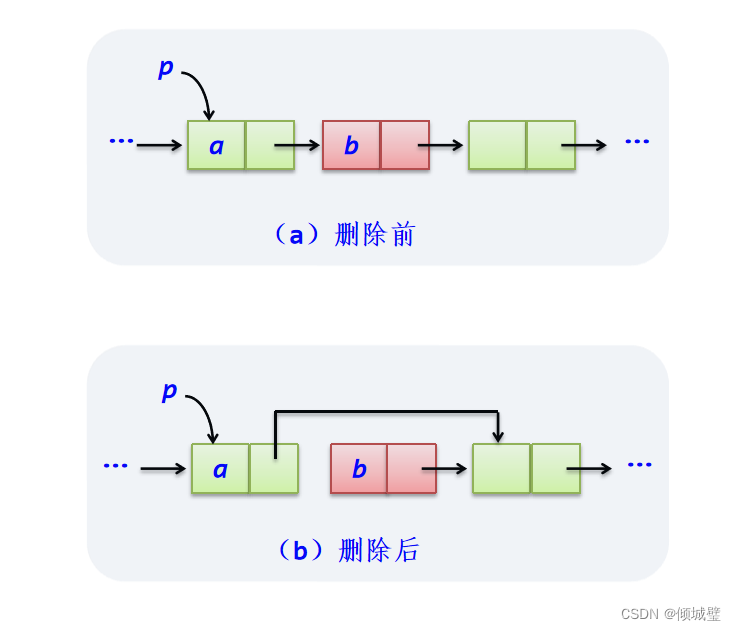
删除节点的算法思路：
1）声明一指针 p 指向链表头结点，初始化 j 从1开始
2）当 j < i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j 累加1
3）若到链表末尾 p 为空，则说明第 i 个结点不存在
4）否则查找成功，将欲删除的结点 p->next 赋值给 q
5） 单链表的删除标准语句 p->next = q->next
6） 将 q 结点中的数据赋值给 e, 作为返回
7） 释放 q 结点
8） 返回成功
// 删除特定值的节点
public void delete(int val) {
if (head == null) {
return;
}
if (head.val == val) {
head = head.next;
} else {
ListNode curr = head;
while (curr.next != null && curr.next.val != val) {
curr = curr.next;
}
if (curr.next != null) {
如果循环结束后，curr.next 不为 null，
说明找到了一个值等于 val 的节点。
这时，将 curr.next 更新为 curr.next.next
这样就将值等于 val 的节点从链表中删除了。
curr.next = curr.next.next;
}
}
}
3.查找倒数第k个元素
class LinkedList{
ListNode head;//链表的头节点
//查找倒数第k个元素
public ListNode findKthFromEndUsingTwoPasses(ListNode head,int k ){
//第一次遍历，计算链表的长度
int length =0;
ListNode current =head;
while(current!=null){
length++;
current=current.next;
}
//如果k大于链表长度，则不存在倒数第k个元素
if (k>length){
throw new IllegalArgumentException("k的值大于链表长度");
}
//第二次遍历，找到第length-k个节点
int index =0;
current =head;
while(current!=null&&index<length-k){
current=current.next;
index++;
}
return current;//返回倒数第j个节点
}
//打印链表节点的值
public void printList(ListNode head){
ListNode current =head;
while(current!=null){
System.out.print(current.val+"->");
current=current.next;
}
System.out.println("null");
}
public static void main(String[] args) {
LinkedList linkedList = new LinkedList();
linkedList.head = new ListNode(1);
linkedList.head.next = new ListNode(2);
linkedList.head.next.next = new ListNode(3);
linkedList.head.next.next.next = new ListNode(4);
linkedList.head.next.next.next.next = new ListNode(5);
System.out.println("Original List:");
linkedList.printList(linkedList.head);
int k = 2; // 假设我们要找倒数第2个元素
ListNode kthNode = linkedList.findKthFromEndUsingTwoPasses(linkedList.head, k);
if (kthNode != null) {
System.out.println("The " + k + "th node from the end has value: " + kthNode.val);
} else {
System.out.println("The " + k + "th node from the end does not exist.");
}
}
}
4.单链表反转
思路分析：
对于这个问题，我们选择迭代的方法，因为他不需要额外的存储空间，并且时间复杂度为O（n）,其中n是链表的长度。
我们使用三个指针，prev初始化为null，以为你它将指向新链表的最后一个节点。即原链表的第一个节点，用于遍历链表，next用于临时存储current的下一个节点。
- 首先我们将current.next保存到next，因为下一步我们需要移动current
- 然后，将current.next指向prev,这是反转链表的关键，它改变了节点的指向，使其指向前一个节点而不是后一个节点。
- 接着，将prev和current向前移动一位，prev变为当前的current，current变为next。
class LinkedList{
ListNode head;//链表的头节点
//反转单链表
public void reverse(){
ListNode prev =null;//初始化prev为null,它将指向反转后的前一个节点
ListNode current= head;//用于遍历当前节点
ListNode next =null;//用于存储下一个节点
while (current!=null){
next=current.next;//在改变current的next之前，先保存下一个节点
current.next=prev;//反转current节点的next指向prev，这是反转的关键步骤
prev=current; //将prev前移一位，现在prev指向current
current=next;//将current前移一位，现在都current指向next
}
head=prev;//完成反转后，prev指向原链表的最后一个节点，即新链表的头节点
}
//打印链表
public void printList(){
ListNode current =head;//头节点开始遍历
while(current!=null){
System.out.println(current.val+"->");
current=current.next;
}
System.out.println("null");
}
}总结：
1.单链表不是随机存储结构
虽然访问单链表第0个节点的时间是O（1）;但是要访问第i个节点，必须从head开始沿着链的方向查找，遍历部分单链表，进行i次都p=p.next操作，时间复杂度为O（n），所以单链表不是随机存储，
从整个算法来说，我们很容易推导出：它们的时间复杂度都是O（n）。如果在我们不知道第i个节点的指针位置 ，单链表数据结构在插入和删除操作上，与线性表的存储结构是没有太大优势的。但如果，我们希望从i个位置，插入10个节点，对于存储结构，意味着，每一次插入都需要移动n-i个节点。每次都是O（n），而单链表，我们只需要在第一次时，找到第i个位置的指针，此时为O（n），接下来只是简单得通过赋值移动指针，时间复杂度都是O（1）。对于插入和删除数据越频繁的操作，单链表的优势越明显。
插入或者删除后驱节点的时间是O(1)，但是前驱节点或者删除自己的时间是O（n）
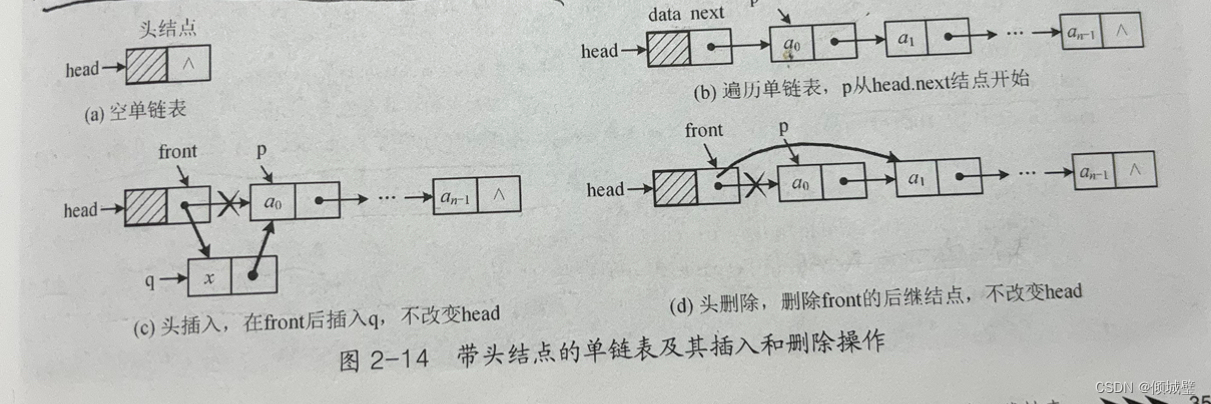
如果front指向单链表中的一个节点，那么插入或者删除后续节点的时间为O（1）。
如果p指向单链表的一个节点，要在p节点前插入一个节点或者删除p节点自己，必须修改p的前驱节点的next域。因此需要再次遍历单链表，找到p前驱节点front，转换为插入或者删除front的后续节点。
下面来做一道题来锻炼一下吧：
题目是使用单链表实现素数线性表
public class PrimeLinkedList {
ListNode head;
public boolean isPrime(int num){
if (num<1){
return false;
}
for (int i =2;i*i<=num;i++){
if (num%i==0){
return false;
}
}
return true;
}
public void insertPrime(int num){
if (!isPrime(num)){
System.out.println(num+"不是素数");
return;
}
ListNode newNode =new ListNode(num);
if (head==null){
head=newNode;
}else{
ListNode current=head;
current =head;
while(current.next!=null){
current=current.next;
}
//这段代码遍历链表到最后一个节点，然后将新的节点连接到链表的末尾
current.next=newNode;
}
}
public void printList() {
ListNode current = head;
while (current != null) {
System.out.print(current.val + " ");
current = current.next;
}
System.out.println();
}
}
class Main {
public static void main(String[] args) {
PrimeLinkedList primeList = new PrimeLinkedList();
// 假设我们想插入以下数字
int[] numbers = {2, 3, 4, 5, 6, 7, 11, 13, 17, 19, 23};
for (int number : numbers) {
primeList.insertPrime(number);
}
primeList.printList();
}
}
