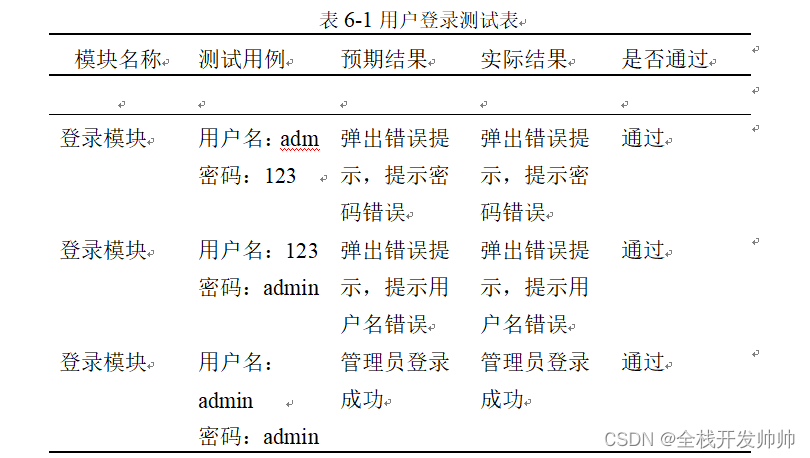
图像卷积
卷积(convolution)是通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与g经过翻转和平移的重叠部分的面积。
卷积概念是两个变量在某范围内相乘后求和的结果。图像处理中的卷积概念:数字图像是一个二维的离散信号,对数字图像做卷积操作其实就是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像的过程。
卷积核的选择规则:1)卷积核大小一般是奇数,这样的话它是按照中间像素点中心对称的,所以卷积核一般都是33,55或者77.有中心了,也有了半径的称呼,例如55大小的核半径就是2。2)卷积核所有元素之和一般要等于1,这是为了原始图像的能量(亮度)守恒。其实也有卷积核元素相加不为1的情况,下面会说到。3)如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但会非常暗。4)对于滤波后的结果,可能会出现负数或者大于255的数值,对于这种情况,我们会将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
不同卷积核下卷积意义:我们经常能看到的平滑、模糊、去噪、锐化、边缘提取等等工作,其实都可以通过卷积操作来完成,举例如下:
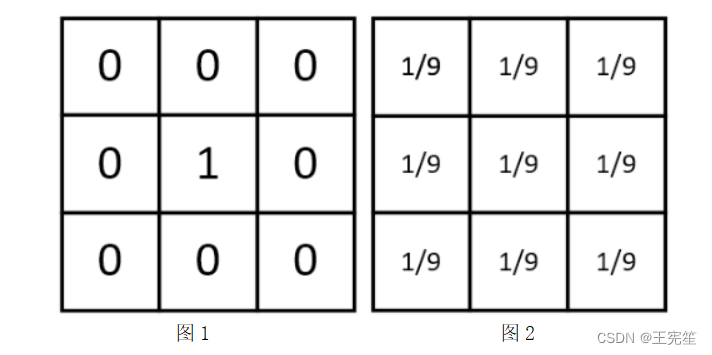
如图1,就是一个没有任何作用的卷积核:将原像素中间像素值乘1,其余全部乘0,显然像素值不会发生任何变化。
如图2,就是平滑均值滤波后选择的卷积核:该卷积核的作用是取卷积核内对应像素点的图像灰度值的平均值代替中间像素的灰度值。
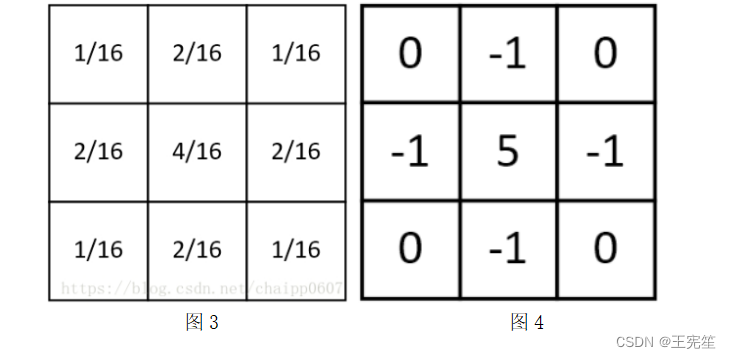
如图3,就是高斯平滑值滤波选择的卷积核:高斯平滑水平和垂直方向呈高斯分布,更突出了中心点在像素平滑后的权重,相比于均值滤波而言,有着更好的平滑效果。
如图4,就是图像锐化选择的卷积核:该卷积核利用的其实是图像中的边缘信息有着比周围像素更高的对比度,而经过卷积后进一步增强了这种对比度,从而使图像显得棱角分明、画面清晰,起到锐化图像的效果。
如图5和6,分别是梯度Prewitt的水平梯度卷积核和垂直梯度卷积核。梯度Prewitt卷积核与