一、滑动窗口概述
滑动窗口(Sliding Window)是一种用于解决数组(或字符串)中子数组(或子串)问题的有效算法。

Sliding Window核心思想:
滑动窗口技术的基本思想是维护一个窗口(一般是一个子数组或子串),该窗口在数组上滑动,并在滑动过程中更新窗口的内容。
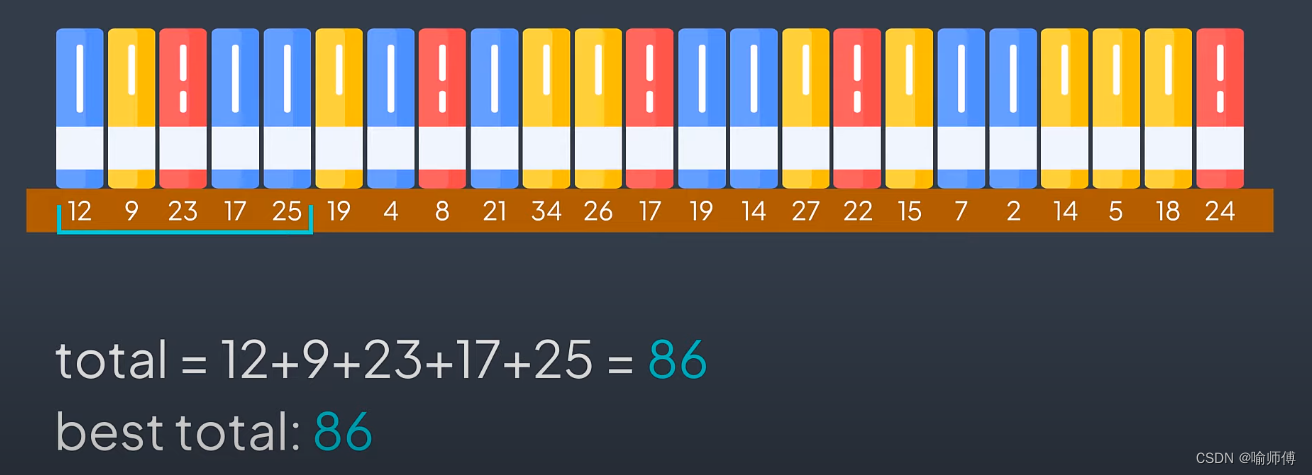

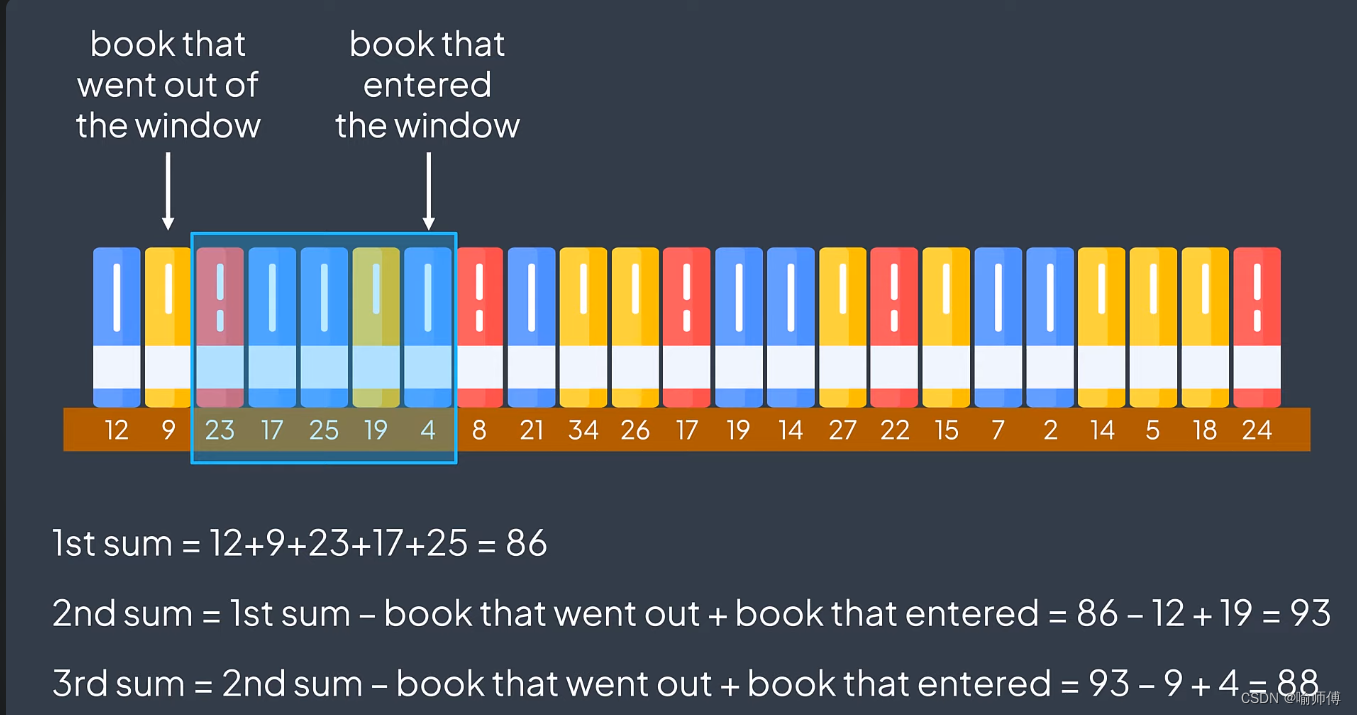
通过滑动窗口,可以在 ( O(n) ) 的时间复杂度内解决很多子数组(子串)问题,其中 ( n ) 是数组(字符串)的长度。
基本步骤:
- 初始化窗口: 定义一个窗口的起始位置和结束位置,通常是两个指针
left和right。 - 滑动窗口: 不断地增加
right指针来扩大窗口,直到窗口满足某个条件为止。

- 更新窗口: 一旦满足条件,尝试缩小窗口大小,即增加
left指针,直到条件不满足为止。 - 记录结果: 在滑动窗口的过程中,根据题目要求来记录最终的结果。
二、习题合集
1.LeetCode 209 长度最小的子数组
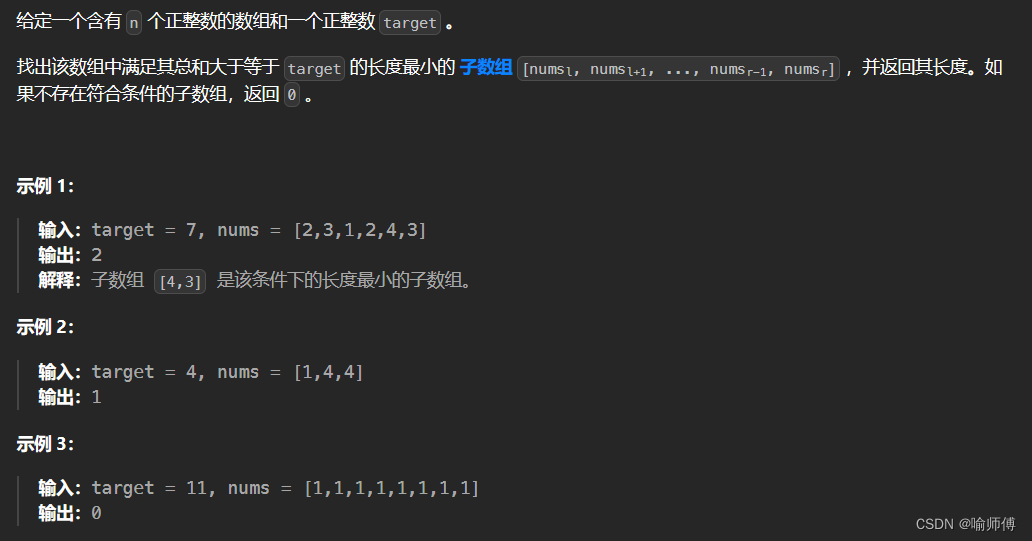
- 滑动窗口O(N)解法:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length; // 数组的长度
int ans = Integer.MAX_VALUE; // 初始化结果为最大值,用于存储最短子数组的长度
int l = 0; // 左指针,指向滑动窗口的起始位置
int sum = 0; // 记录滑动窗口内元素的和
for (int r = 0; r < n; r++) { // 右指针,扩展滑动窗口
sum += nums[r]; // 将右指针指向的元素加入窗口
while (sum >= target) { // 当窗口内元素和大于等于目标值时,尝试缩小窗口
ans = Math.min(ans, r - l + 1); // 更新最短子数组的长度
sum -= nums[l]; // 缩小窗口,左指针向右移动,减少窗口内的元素和
l++; // 左指针右移
}
}
return ans == Integer.MAX_VALUE ? 0 : ans; // 如果找不到满足条件的子数组,返回0;否则返回最短子数组的长度
}
}
2.LeetCode 3 无重复字符的最长子串
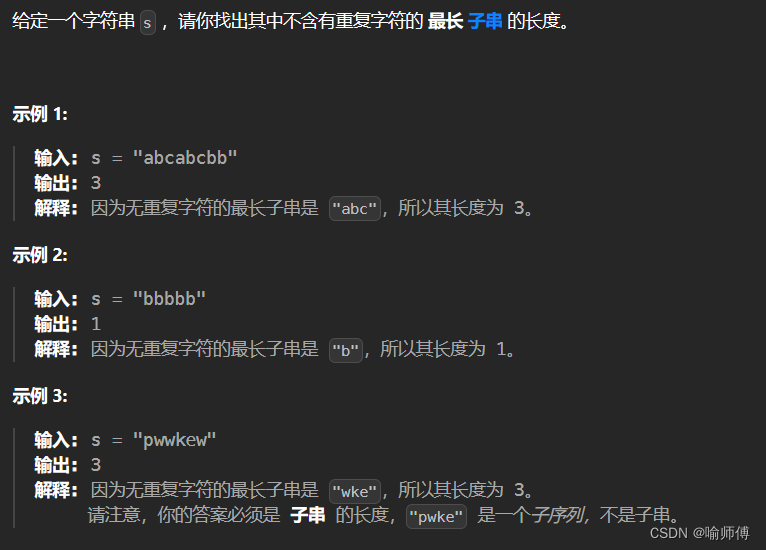
- 第一版滑动窗口
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map = new HashMap<>(); // 创建一个哈希表,用来记录字符及其出现的最后位置
int n = s.length(); // 字符串的长度
int l = 0, ans = 0; // l表示当前不重复子串的起始位置,ans用来记录最长不重复子串的长度
for (int r = 0; r < n; r++) {
char c = s.charAt(r); // 获取当前字符
if (map.containsKey(c)) {
//如果曾经出现的 字母 还在窗口内 —— l更新到 该位置+1
//如果曾经出现的 字母 已不在当前窗口内了—— 则不需要更新
l = Math.max(l,map.get(c)+1);
}
map.put(c, r); // 更新当前字符的最后出现位置为当前索引r
ans = Math.max(ans, r - l + 1); // 更新最长不重复子串的长度
}
return ans; // 返回最长不重复子串的长度
}
}
要理解 left = Math.max(left,map.get(s.charAt(i)) + 1);需要回归到滑动窗口的原理上。
窗口中始终是无重复字母的字符串。 我们通过窗口的左界和右界控制窗口。
右界不用特意操作,因为它是+1,+1地涨上去,记得在循环里+1就好。
左界:每当有一个字符曾经出现过,就需要判断左界。
重点来了:
若,被判断的字符上一次出现的位置就在滑动窗口内,即 [ i,j ] 内, 则需要left改变位置,改变为该字符上次出现位置+1。也就是left = map.get(s.charAt(i)) + 1的情况。
例如:
abcdb中,窗口正常运行到abcd时,下一个字符为b,b上一次出现在实在窗口里,所以需要把left设置为上一次出现的位置+1的位置,得到新的窗口为cdb,不然你不这样设置,窗口里有重复的字符(bcdb),不符合窗口的定义。
若,不在滑动窗口内,则不用管。 不用管是因为:窗口中字符串没有重复字符。窗口符合定义。所以left = left。 left = left就表示这个窗口暂时不变。
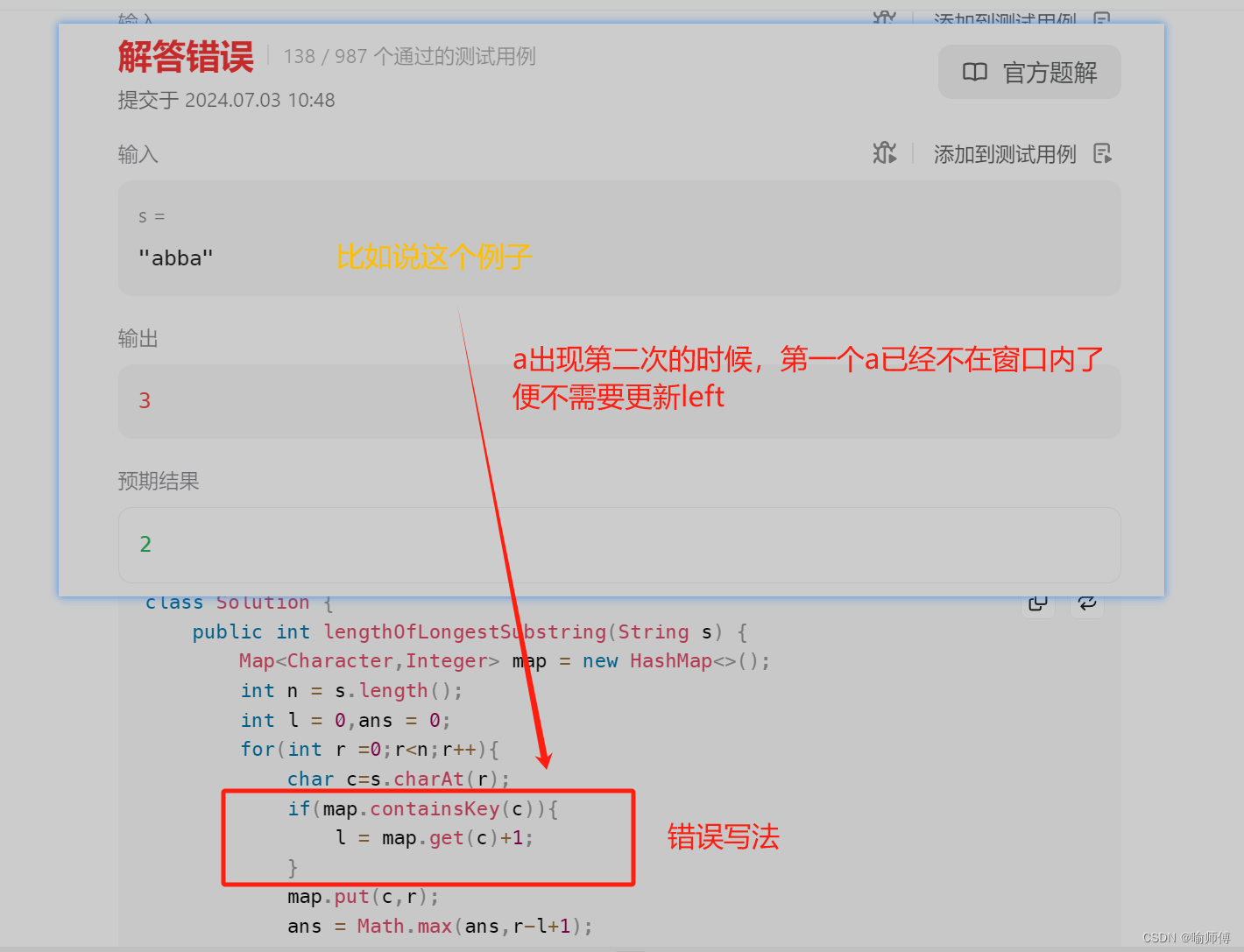
- 第二版优化的滑动窗口:
class Solution {
public int lengthOfLongestSubstring(String s) {
// 记录字符上一次出现的位置
int[] last = new int[128]; // 创建一个长度为128的整型数组,用来记录ASCII码表中每个字符上一次出现的位置
for(int i = 0; i < 128; i++) {
last[i] = -1; // 初始化数组,所有字符的上一次出现位置都设为-1,表示尚未出现过
}
int n = s.length(); // 字符串s的长度
int res = 0; // 用于记录最长的不重复子串的长度
int start = 0; // 窗口开始位置,用来维护当前不重复子串的起始位置
for(int i = 0; i < n; i++) {
int index = s.charAt(i); // 获取当前字符的ASCII码作为索引
start = Math.max(start, last[index] + 1); // 更新窗口的起始位置,确保不重复的起点
res = Math.max(res, i - start + 1); // 更新最大的不重复子串长度
last[index] = i; // 更新当前字符的最后出现位置为当前索引i
}
return res; // 返回最长的不重复子串的长度
}
}
3.LeetCode 187 重复的DNA序列
- 哈希表法~
class Solution {
public List<String> findRepeatedDnaSequences(String s) {
List<String> ans = new ArrayList<>(); // 用于存放重复的DNA序列
int n = s.length();
if (n < 10) return ans; // 如果字符串长度小于10,直接返回空列表,因为无法形成长度为10的序列
Map<String, Integer> map = new HashMap<>(); // 创建一个哈希表,用来记录每个长度为10的子序列及其出现的次数
map.put(s.substring(0, 10), 1); // 初始化,将第一个长度为10的子序列放入哈希表中
for (int i = 1; i + 10 <= n; i++) { // 从第二个子序列开始遍历到倒数第十个子序列
String ss = s.substring(i, i + 10); // 获取当前长度为10的子序列
if (map.getOrDefault(ss, 0) == 1) { // 如果该子序列已经在哈希表中出现过一次
ans.add(ss); // 将该子序列加入结果列表
}
map.put(ss, map.getOrDefault(ss, 0) + 1); // 更新哈希表中该子序列的出现次数
}
return ans; // 返回重复的DNA序列列表
}
}
- 滑动窗口法~
class Solution {
// 滑动窗口法查找重复的长度为10的DNA序列
public List<String> findRepeatedDnaSequences(String s) {
List<String> ans = new ArrayList<>(); // 用于存放重复的DNA序列
int n = s.length(); // 字符串的长度
if (n < 10) return ans; // 如果字符串长度小于10,直接返回空列表,因为无法形成长度为10的序列
StringBuilder sb = new StringBuilder(s.substring(0, 10)); // 初始化第一个长度为10的子串
Set<String> set = new HashSet<>(); // 使用集合来记录出现过的子串
set.add(sb.toString()); // 将第一个子串添加到集合中
for (int i = 1; i + 10 <= n; i++) {
String str = s.substring(i, i + 10); // 获取当前长度为10的子串
if (set.contains(str)) { // 如果集合中已经包含当前子串
if (!ans.contains(str)) // 且列表中还未包含该子串
ans.add(str); // 将该子串添加到列表中
} else { // 如果集合中不包含当前子串
set.add(str); // 将当前子串添加到集合中
}
}
return ans; // 返回存放了重复DNA序列的列表
}
}
4.LeetCode 424 替换后的最长重复字符

- 核心思想:
相同的最长子字符串(窗口) = 窗口内最大字符个数 + 反转次数
一旦 窗口长度 - 窗口内最大字符个数 > 反转次数 窗口开始移动
public int characterReplacement(String s, int k) {
int n = s.length();
if(n<2) return n;
int ans = 0; // 用于存储最长连续相同字符的子串的长度
int maxFreq = 0; // 用于存储当前窗口内出现次数最多的字符的次数
char[] c = s.toCharArray();
int[] freq = new int[26]; // 记录当前窗口内每个字符出现的次数
int left = 0; // 滑动窗口的左边界
for (int right = 0; right < n; right++) {
++freq[c[right] - 'A']; // 更新右边界字符的出现次数
maxFreq = Math.max(maxFreq, freq[c[right] - 'A']); // 更新最大出现次数
// 如果当前窗口的大小减去出现次数最多的字符的次数大于k,则需要缩小窗口
// 使得窗口内可以通过替换字符使其变成连续相同字符的子串
if (right - left + 1 > maxFreq + k) {
freq[c[left] - 'A']--; // 缩小窗口时,更新左边界字符的出现次数
left++; // 缩小窗口
}
// 更新最长连续相同字符的子串的长度
ans = Math.max(ans, right - left + 1);
}
return ans;
}
5.LeetCode 438 找到字符串中所有字母异位词
- 详细的思路都在注释里面了哈~
public List<Integer> findAnagrams(String s, String p) {
//在长度为26的int数组target中存储字符串p中对应字符(a~z)出现的次数
//如p="abc",则target为[1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
//如p="bbdfeee",则target为[0,2,0,1,3,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
int[] target = new int[26];
for (int i = 0; i < p.length(); i++) {
target[p.charAt(i) - 'a']++;
}
//双指针构建滑动窗口原理:
//1.右指针right先向右滑动并在window中存储对应字符出现次数
//2.当左右指针间的字符数量(包括左右指针位置的字符)与p长度相同时开始比较
//3.比较完成后,左右指针均向右滑动一位,再次比较
//4.以后一直重复2、3,直到end指针走到字符串s的末尾
int left = 0, right = 0;
int[] window = new int[26];//构建一个与target类似的,存储了字符串s从left位置到right位置的窗口中字符对应出现次数的数组
List<Integer> ans = new ArrayList<Integer>();
while (right < s.length()) {
window[s.charAt(right) - 'a']++;//每次右指针right滑动,字符串s的right位置的字符出现次数加1
if (right - left + 1 == p.length()) {
if (Arrays.equals(window, target)) ans.add(left);//通过Arrays.equals方法,当window数组与target数组相等即为异或词
window[s.charAt(left) - 'a']--;//比较完成后,字符串s的left位置的字符出现次数减1(减1是因为左指针下一步要向右滑动)
left++;//左指针向右滑动
}
right++;//右指针向右滑动
}
return ans;
}
6.LeetCode 567 字符串的排列
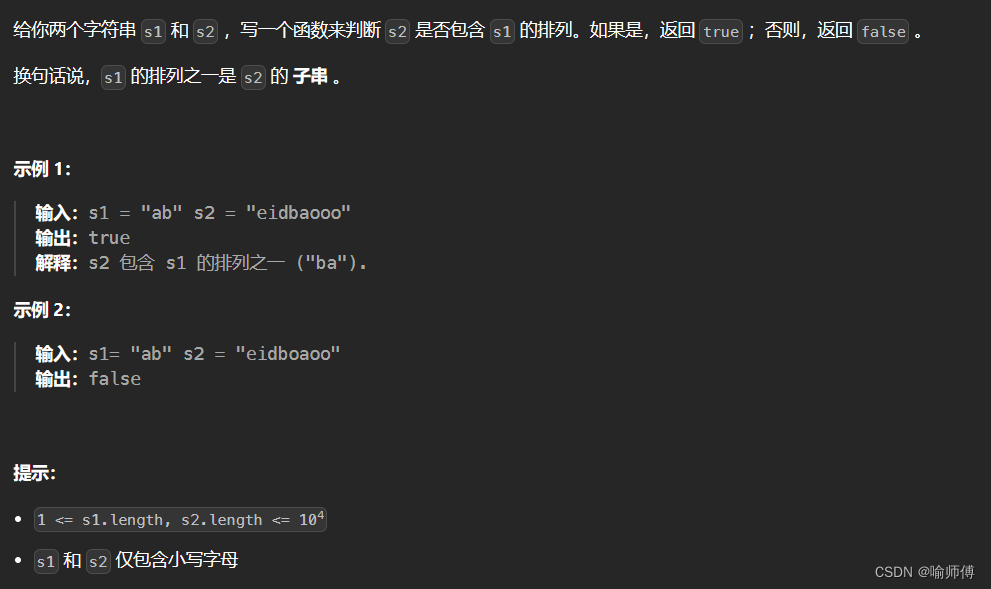
这道题其实跟上一题有异曲同工之妙~🤣
- 直接贴代码啦~ 思路在注释里~
class Solution {
public boolean checkInclusion(String s1, String s2) {
int n = s2.length();
if (n < s1.length())
return false; // 如果 s2 的长度小于 s1 的长度,直接返回 false,因为无法包含 s1 的排列
int[] target = new int[26]; // 目标字符串 s1 的字符频率统计数组
for (char c : s1.toCharArray()) {
++target[c - 'a']; // 统计 s1 中每个字符的出现次数
}
int l = 0, r = 0;
int[] window = new int[26]; // 滑动窗口中的字符频率统计数组
while (r < n) {
++window[s2.charAt(r) - 'a']; // 将 s2 中当前右边界字符加入窗口,并增加计数
if (r - l + 1 == s1.length()) { // 当窗口大小等于 s1 的长度时进行判断
if (Arrays.equals(target, window)) {
return true; // 如果窗口内的字符频率与 s1 相同,则找到了 s1 的一个排列,返回 true
} else {
--window[s2.charAt(l) - 'a']; // 否则,移动左边界,将左边界字符移出窗口,并减少计数
++l; // 左边界右移,缩小窗口
}
}
++r; // 右边界右移,扩大窗口
}
return false; // 扫描完整个字符串 s2 后没有找到 s1 的排列,返回 false
}
}
7. LeetCode 和相同的二元子数组

- 前缀和+哈希表法~

要找到全部的子数组和为goal,直觉上我们需要找到所有前缀和里的i和j
满足presum[j] - presum[i] == goal——但是这样找i和j需要遍历两次,是O(N2 )的。
故采取哈希表存储前面的所有presum[i] == presum[j] - goal的个数,答案累加即可。
因为只有0和1,所以本题前缀和其实也是统计1的个数。
public int numSubarraysWithSum(int[] nums, int goal) {
int sum = 0;
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
int ret = 0;
for (int num : nums) {
cnt.put(sum, cnt.getOrDefault(sum, 0) + 1); // 记录当前累积和 sum 的出现次数
sum += num; // 更新累积和 sum
// 统计以当前位置为结束位置,和为 sum - goal 的子数组个数
ret += cnt.getOrDefault(sum - goal, 0);
}
return ret;
}
-
sum:累积和,表示从数组开始到当前位置的所有元素之和。对于数组nums中的每个元素num,更新累积和sum。 -
cnt:HashMap,用于记录每个累积和出现的次数。 -
ret:最终的返回结果,表示和为goal的子数组的个数。 -
在更新
sum后,查看cnt中是否有sum - goal这个累积和的记录。如果有,则表示从之前某个位置到当前位置,存在一个子数组的和为goal。累加这个值到ret中。 -
sum - goal —>pre[j] - goal ,即找到了pre[i]。 pre[j] - pre[i] = goal。
Eg.
假设输入数组 nums = [1, 0, 1, 0, 1],goal = 2。
for (int num : nums) {
cnt.put(sum, cnt.getOrDefault(sum, 0) + 1); // 记录当前累积和 sum 的出现次数
sum += num; // 更新累积和 sum
// 统计以当前位置为结束位置,和为 sum - goal 的子数组个数
ret += cnt.getOrDefault(sum - goal, 0);
}
-
第一个元素
1:- 更新
sum = 1。 count更新为{0: 1, 1: 1},表示累积和为0和1各出现了1次。- 此时
sum - goal = -1,在count中没有-1的记录,所以不更新result。
- 更新
-
第二个元素
0:- 更新
sum = 1。 count更新为{0: 1, 1: 2},表示累积和为0出现了1次,累积和为1出现了2次。- 此时
sum - goal = -1,在count中没有-1的记录,所以不更新result。
- 更新
-
第三个元素
1:- 更新
sum = 2。 count更新为{0: 1, 1: 2, 2: 1},表示累积和为0出现了1次,累积和为1出现了2次,累积和为2出现了1次。- 此时
sum - goal = 0,在count中有0的记录,所以更新result += 1,此时result = 1。
- 更新
-
第四个元素
0:- 更新
sum = 2。 count更新为{0: 1, 1: 2, 2: 2},表示累积和为0出现了1次,累积和为1出现了2次,累积和为2出现了2次。- 此时
sum - goal = 0,在count中有0的记录,所以更新result += 1,此时result = 2。
- 更新
-
第五个元素
1:- 更新
sum = 3。 count更新为{0: 1, 1: 2, 2: 2, 3: 1},表示累积和为0出现了1次,累积和为1出现了2次,累积和为2出现了2次,累积和为3出现了1次。- 此时
sum - goal = 1,在count中有1的记录,所以更新result += count[sum - goal],即result += count[1] = 2,此时result = 4。
- 更新
- 结果:
- 最终返回
result = 4,表示数组nums中和为2的子数组有4个,分别是[1,0,1]、[1,0,1,0]、[0,1,0,1]、[1,0,1]。
- 最终返回
- 滑动窗口~

class Solution {
public int numSubarraysWithSum(int[] nums, int goal) {
int n = nums.length;
// left1与left2之间夹着的是很多个0
int left1 = 0, left2 = 0, right = 0;
int sum1 = 0, sum2 = 0;
int res = 0;
// 右边界
while (right < n) {
sum1 += nums[right];
// sum1 要等于 goal+1
while (left1 <= right && sum1 > goal) {
sum1 -= nums[left1];
left1++;
}
sum2 += nums[right];
// sum2 要等于 goal
while (left2 <= right && sum2 >= goal) {
sum2 -= nums[left2];
left2++;
}
// 其中的每个0都能算一种情况
res += left2 - left1;
// 右指针右移
right++;
}
return res;
}
}

更新于: