前提

• 最近闲着没事
• 就看了计算几何的一些知识

构建凸包

Incremental Construction

• 复杂度为O(n²)
• 原理就是不停蚕食下一个合适的点。判断原理是，第X个极点和前n个极点构成的多边形会有切点S，T。
  
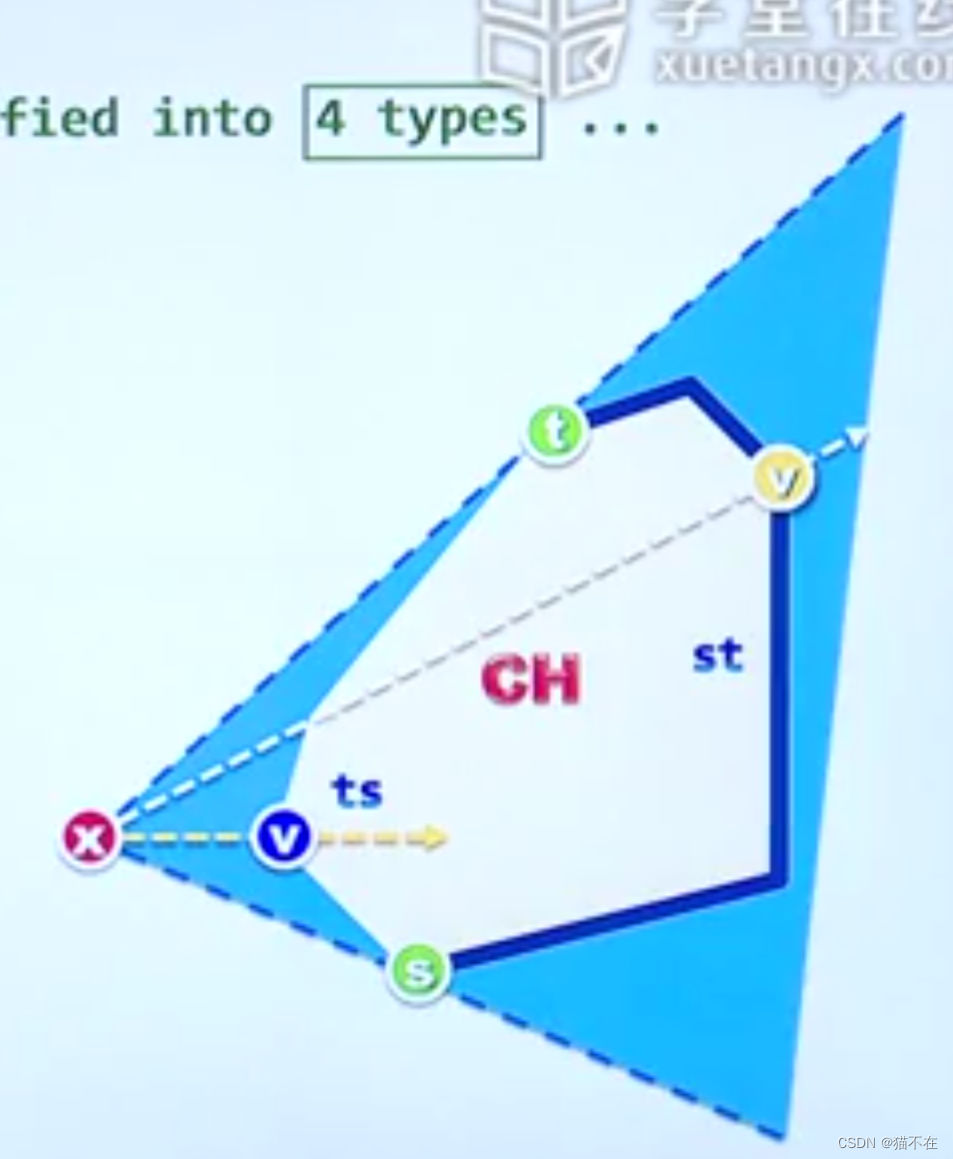
• 和这两个点的连线，把原先多边形分成两个区域
• 对于每一个点都有一个前驱和后继，
• 将每一个点和x连线，然后判断该点的前驱和后继相对该连线的左右方位。会得到如下模式
• st区域是左右
• ts区域是右左
• s点是左左
• t点是右右

Javas March方法

• 复杂度为O(n²)
• 原理就是，不停的寻找下一个合适的极点，通过逐步蚕食的策略构建凸包。
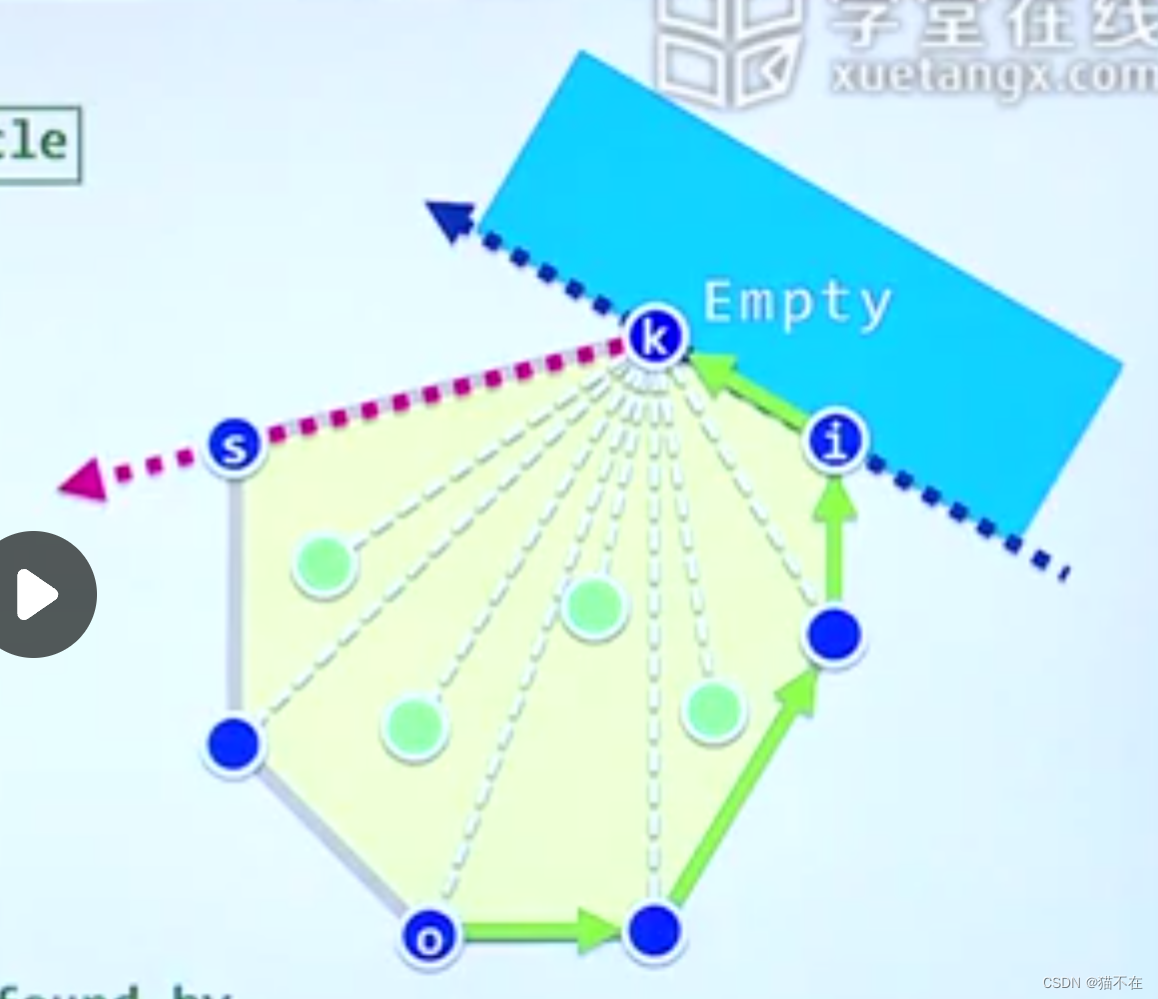
• 在寻找第s个点的时候，s和k构成极边，众所周知，剩下的点都在极边的另一边
• 所以我们遍历剩下的每一个点，假设这个点是极点s
• 如果找到相比ks更靠左的点就替换当前点作为s，继续判断。
• 一直到结束
  

Graham Scan算法

• 它的原理也很简单
• 先做预排序
• 就是找到一个极点，然后把剩下的点和他形成的极角来排序
  
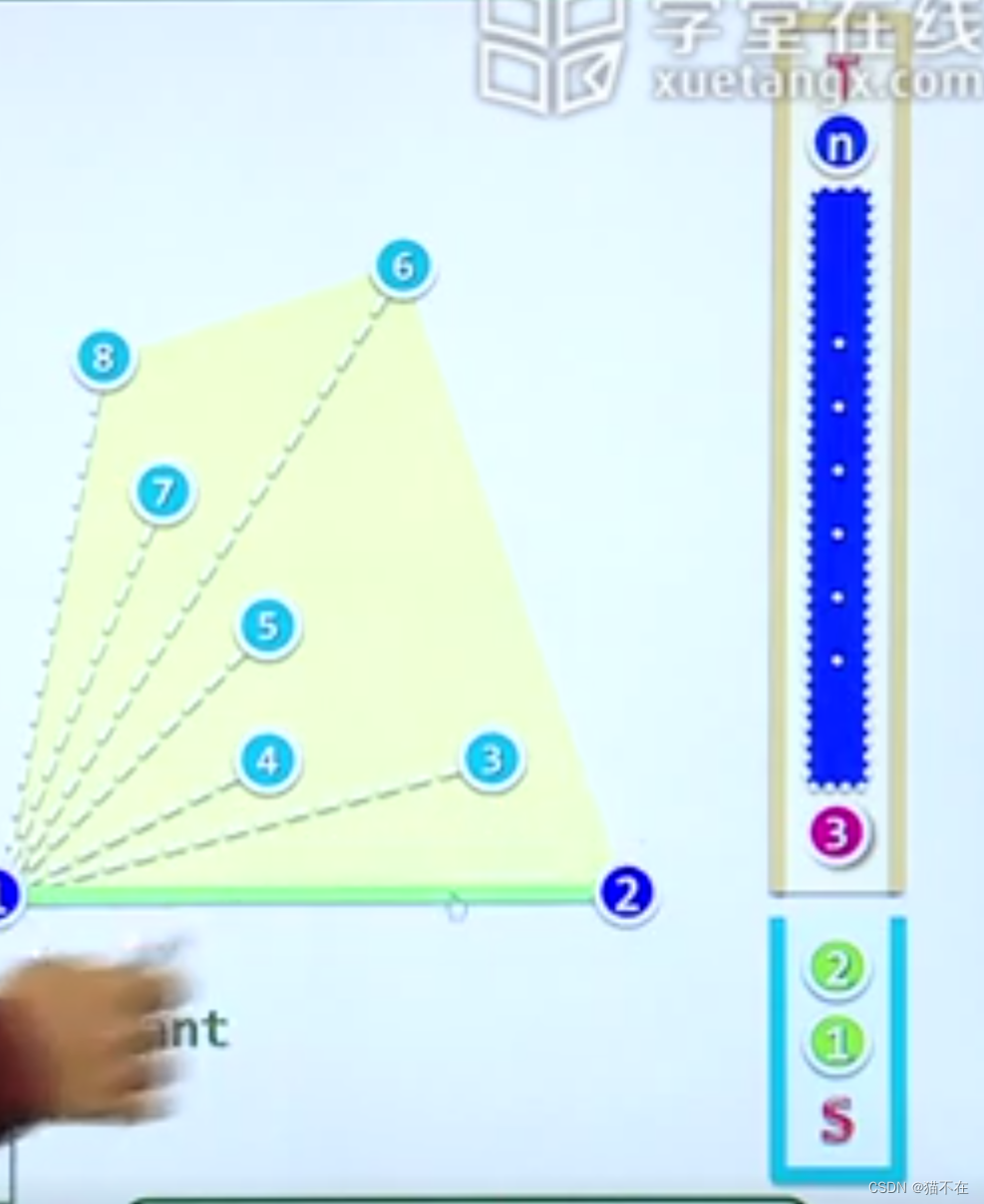
• 准备两个栈，T栈的出口对着S栈的入口
• S栈的入口先放入1和2两个点，把剩余点全部放入T栈中
• 1拿到T栈栈顶第一个元素T1
• 2判断T1是否在S1->S2连成的线的左边
• 3在，就说明当下是极点，放入S栈，继续步骤1
• 4不在，就把S栈元素S1出栈，继续步骤2
• 最终S栈的所有元素，从栈底到栈顶就是所有构成凸包的所有极点。