为了应对订单修改的场景，电商ERP系统应该如何设计相应模块？

电商ERP系统，经常遇到需要修改订单的情况，修改订单主要以下几种场景：

一、修改商品

修改商品，包括对正常商品的换货、以及对赠品的增删改。

1. 正常商品换货

在日常电商活动过程中，顾客可能由于个人情况需要换品，比如换尺码、规格、颜色等，此时ERP系统中需要支持。

但店铺是否支持商品换货，在ERP系统中要做好参数设置，以防订单管理员操作失误。

在ERP系统中，限制换货商品有时候也需要考虑换货的商品价格与当前商品的价格情况，正常换货后的商品价格要<=当前商品的价格。

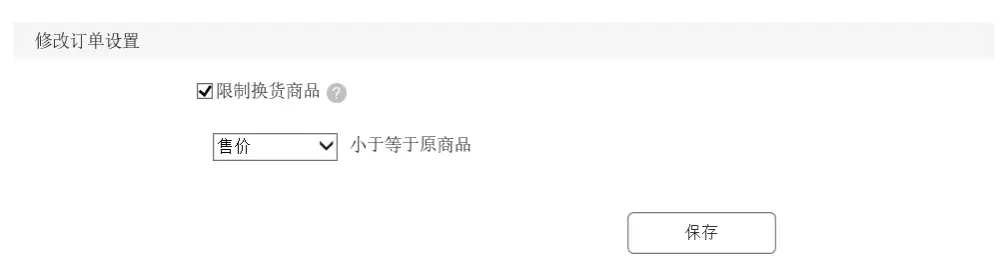
在换货场景中，ERP系统还需要考虑支持预售商品、套装商品、套装中的单品的换货。

不同的订单状态，商品换货后的库存增减也要注意。
换货后，商品在订单中的分摊金额要注意继承，订单重量要重新计算。

2. 赠品增删改

赠品增删改，是指赠品的添加、删除、修改，修改赠品即换赠品，与上述换商品逻辑基本一致。

赠品的添加/删除，可对订单进行批量添加，也可单个添加，也可添加指定数量的赠品。

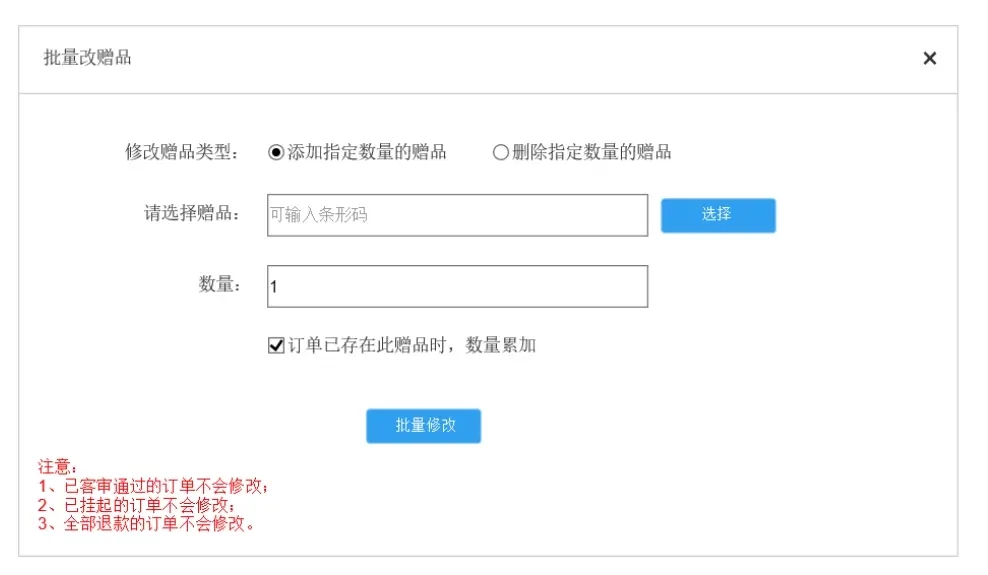
赠品的添加/删除，要注意订单状态，也要注意挂起的订单、退款的订单。

赠品的添加/删除成功后，要注意修改赠品库存，订单重量要重新计算。

二、改仓库、改快递

改仓库、改快递也是电商ERP系统中非常常见的功能，系统要支持针对订单的单个或者批量修改。

1. 改仓库

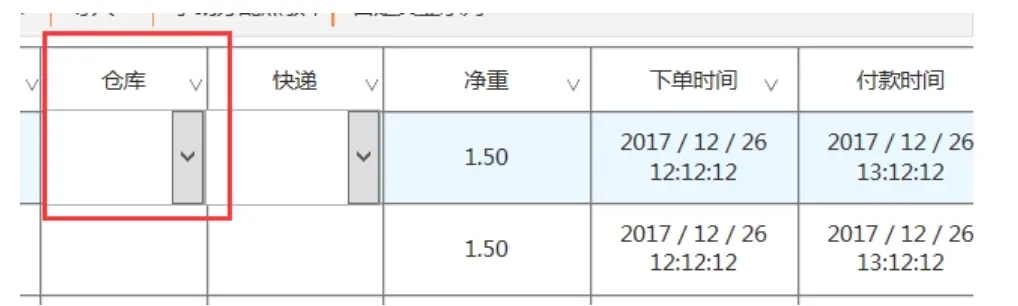
改仓库时，要注意订单状态，一般客审前，可直接修改仓库，客审后，修改仓库成功后，要注意做标记，防止被智能分仓功能刷掉。

改仓库时，要注意仓库与快递的绑定关系，若订单已经指定快递，而指定的快递未绑定此仓库，则会出现修改失败，同时要将修改失败原因的日志更新到系统中。

修改仓库成功后，要注意台账库存的修改。

2. 改快递

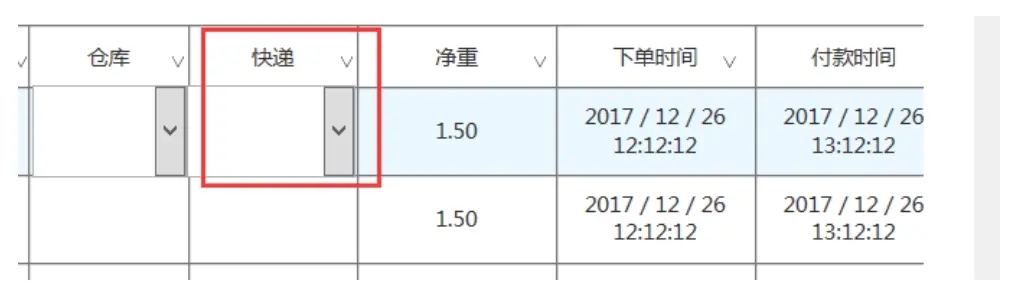
改快递时：

首先要注意，仓库是否指定，若指定，则要注意快递与仓库的绑定关系。

其次，改快递要注意调用平台的快递可达接口，判断快递是否可达。

再次，要注意清空快递单号，若为电子面单，支持的平台若存在回收电子面单号接口，则要调用回收电子面单号接口。

另外，若订单为货到付款，则修改的快递要支持货到付款。

三、修改订单信息

1. 修改订单的收货信息：在电商ERP系统设计中，订单修改还支持修改订单中的收货信息，包括收货人、地址等信息，不过因目前各大平台已经完成订单信息加密，收货信息的修改直接对接平台接口完成修改即可。

2. 修改订单的内部标签：内部标签一般是ERP系统订单管理员对订单进行的备注，故要支持修改。

3. 修改订单的仓审须知：仓审须知是指订单需要仓库人员注意的备注，要支持修改。

4. 其他，每个电商ERP系统的订单设计结构不一致 ，在设计时要注意可修改的字段即可。