线性判别分析（Linear Discriminant Analysis, LDA）是一种用于模式识别和机器学习的分类和降维技术。LDA通过找到能最大化类别间方差和最小化类别内方差的投影方向，实现样本的降维和分类。

LDA的基本思想

LDA的核心思想是通过线性变换将数据投影到一个新的空间中，使得同一类别的样本尽可能地紧凑在一起，而不同类别的样本尽可能地分开。具体来说，LDA的目标是找到一个或多个线性判别向量，使得类内散度矩阵（within-class scatter matrix）最小化，而类间散度矩阵（between-class scatter matrix）最大化。

LDA的数学公式

1. 类内散度矩阵（Within-class scatter matrix）:

其中，(S_i) 表示第 (i) 类的散度矩阵，计算方式为:

(mu_i) 是第 (i) 类的均值向量，(C_i) 是第 (i) 类的样本集合。

1. 类间散度矩阵（Between-class scatter matrix）:

   其中，(N_i) 是第 (i) 类的样本数量，(mu_i) 是第 (i) 类的均值向量，(mu) 是所有样本的全局均值向量。

2. 线性判别准则: 通过求解以下特征值问题来找到投影向量:

   其中，(w) 是判别向量，(\lambda) 是对应的特征值。最大的特征值对应的特征向量是最佳投影方向。

LDA的步骤

1. 计算每个类别的均值向量。

2. 计算类内散度矩阵和类间散度矩阵。

3. 求解特征值和特征向量，找到最佳投影方向。

4. 将数据投影到新的空间，进行分类或降维。

LDA的应用

• 分类问题：LDA可以用于二分类或多分类问题，常用于人脸识别、文本分类等领域。

• 降维问题：LDA可以用于数据降维，特别是当类别标签已知时，通过LDA可以实现有监督的降维。

LDA的优缺点

优点：

• 考虑类别信息，适合用于分类任务。

• 计算效率高，适用于高维数据。

缺点：

• 适用于线性可分的情况，对于非线性数据效果不好。

• 对数据的均值和协方差矩阵的假设较强，要求数据符合高斯分布。

基于Python的LDA可视化实例

我们使用 Wine 数据集进行 LDA 降维并进行可视化。这里是一个完整的代码示例，包括数据加载、标准化、LDA降维和降维前后的可视化。

Wine 数据集是一个经典的机器学习数据集，常用于分类和降维任务。它包含了不同化学分析数据，用于识别葡萄酒的三个不同类别。这个数据集最早由 Riccardo Leardi 和 Michelangelo Grillo 在 1991 年介绍，广泛用于机器学习和数据挖掘研究。

数据集概述

Wine 数据集中的样本是从意大利某个地区生长的葡萄酿造的葡萄酒中提取的，涉及 13 种化学成分分析。数据集包含 178 个样本，每个样本有 13 个特征。

数据集的特征

Wine 数据集的特征及其含义如下：

1. Alcohol：酒精含量

2. Malic acid：苹果酸

3. Ash：灰分

4. Alcalinity of ash：灰分的碱度

5. Magnesium：镁含量

6. Total phenols：总酚含量

7. Flavanoids：类黄酮

8. Nonflavanoid phenols：非类黄酮酚

9. Proanthocyanins：原花青素

10. Color intensity：颜色强度

11. Hue：色调

12. OD280/OD315 of diluted wines：稀释酒的OD280/OD315

13. Proline：脯氨酸

类别

数据集中的目标变量（label）有三个类别，分别代表三个不同的葡萄酒品种：

1. 类别 0：葡萄酒品种 1

2. 类别 1：葡萄酒品种 2

3. 类别 2：葡萄酒品种 3

数据集结构

数据集共有 178 个样本，具体分布如下：

• 类别 0：59 个样本

• 类别 1：71 个样本

• 类别 2：48 个样本

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.preprocessing import StandardScaler
import open3d as o3d

# 加载 Wine 数据集
wine = load_wine()
X = wine.data
y = wine.target
target_names = wine.target_names

# 数据标准化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# 使用 Open3D 进行降维前的三维可视化
def visualize_3d(X, y, target_names):
    colors = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]], dtype=float)  # red, green, blue
    point_colors = colors[y]
    
    pcd = o3d.geometry.PointCloud()
    pcd.points = o3d.utility.Vector3dVector(X[:, :3])  # 仅使用前 3 个特征进行三维可视化
    pcd.colors = o3d.utility.Vector3dVector(point_colors)
    
    vis = o3d.visualization.Visualizer()
    vis.create_window()
    vis.add_geometry(pcd)
    vis.run()
    vis.destroy_window()

# 可视化降维前的三维数据
visualize_3d(X_std, y, target_names)

# 进行 LDA 降维
lda = LDA(n_components=2)
X_lda = lda.fit_transform(X_std, y)

# 可视化降维后的数据
plt.figure(figsize=(8, 6))
colors = ['red', 'green', 'blue']
markers = ['o', 's', 'D']

for color, marker, i, target_name in zip(colors, markers, [0, 1, 2], target_names):
    plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], alpha=0.8, color=color, marker=marker, label=target_name)
    
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of Wine Dataset')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.show()

原始点云：

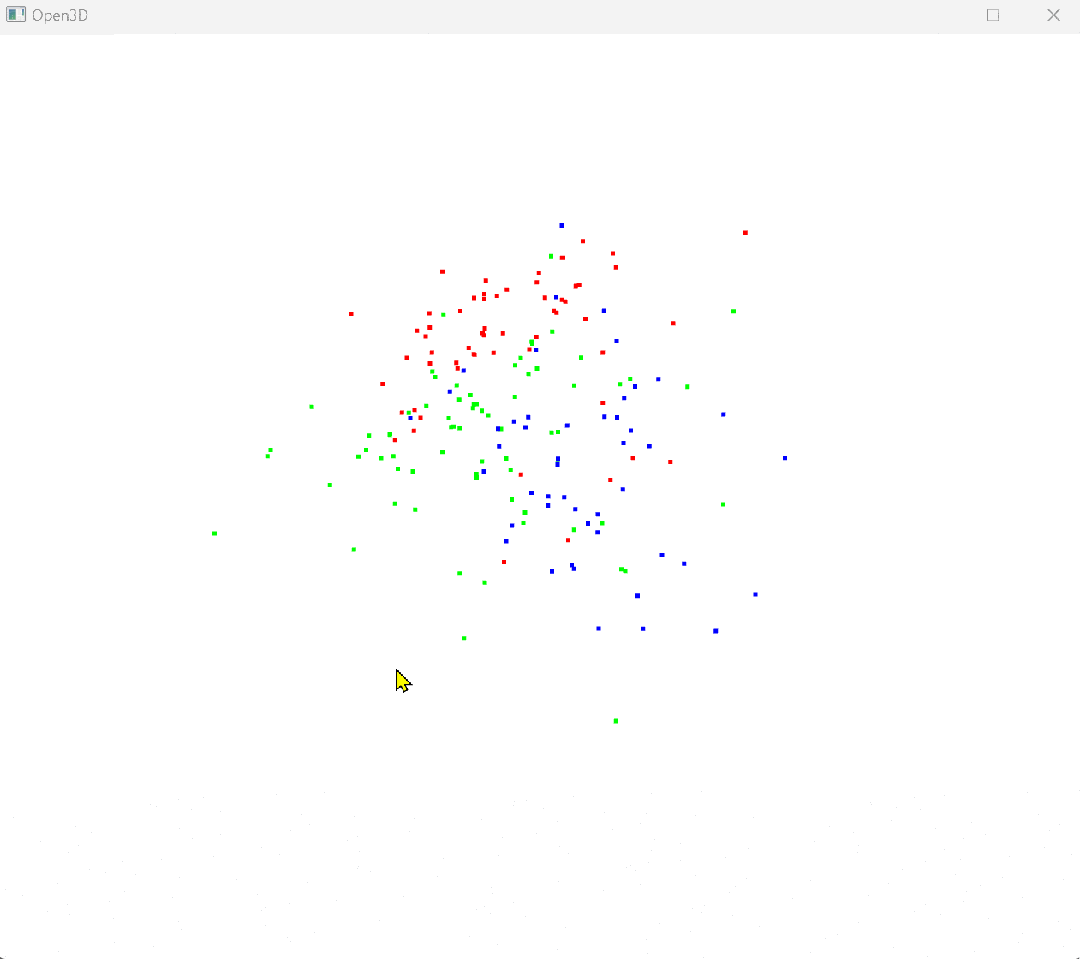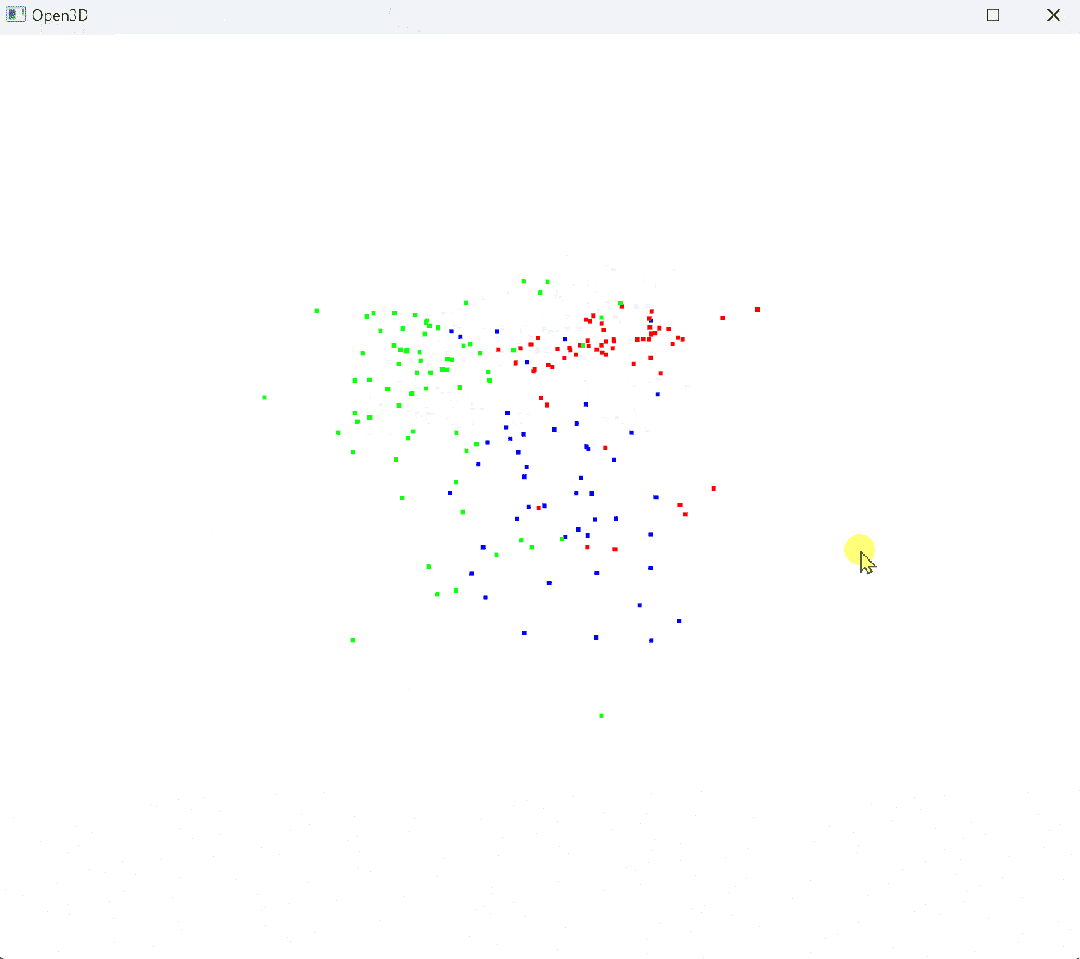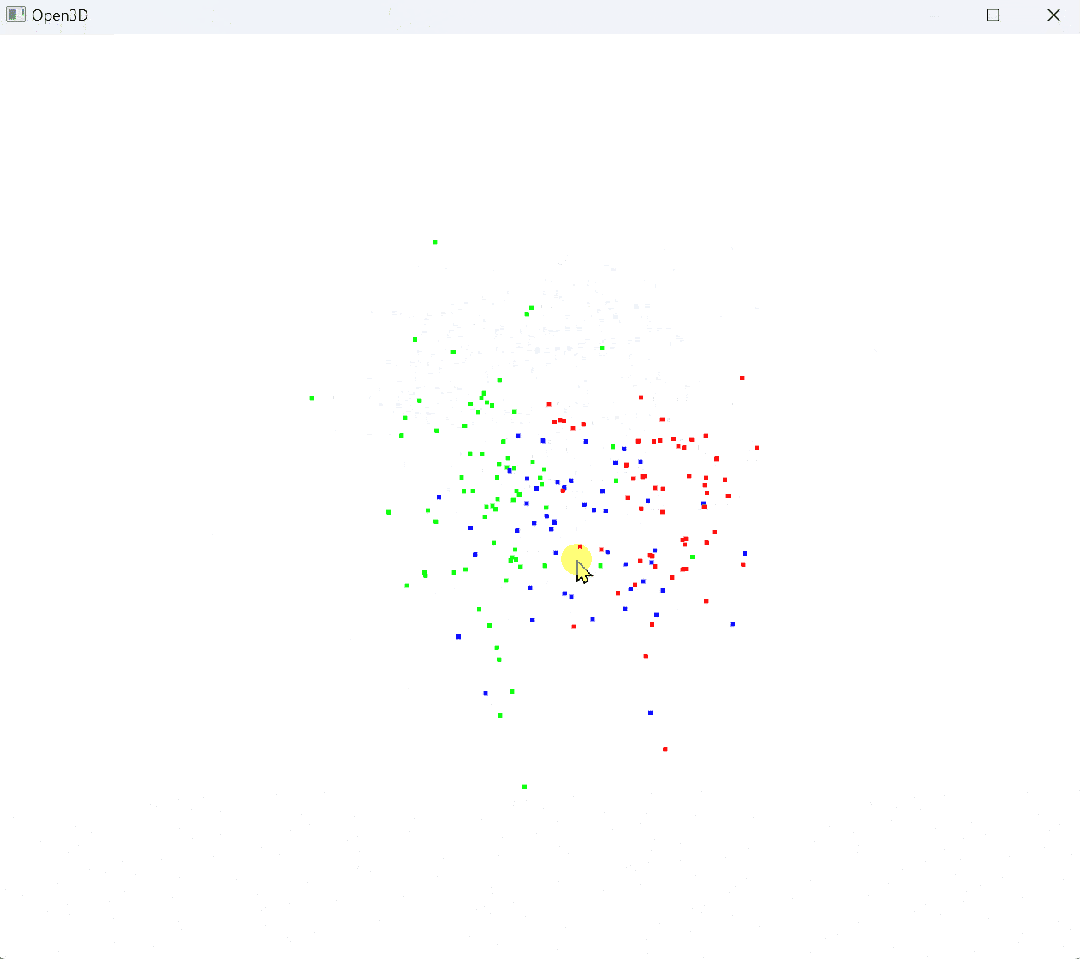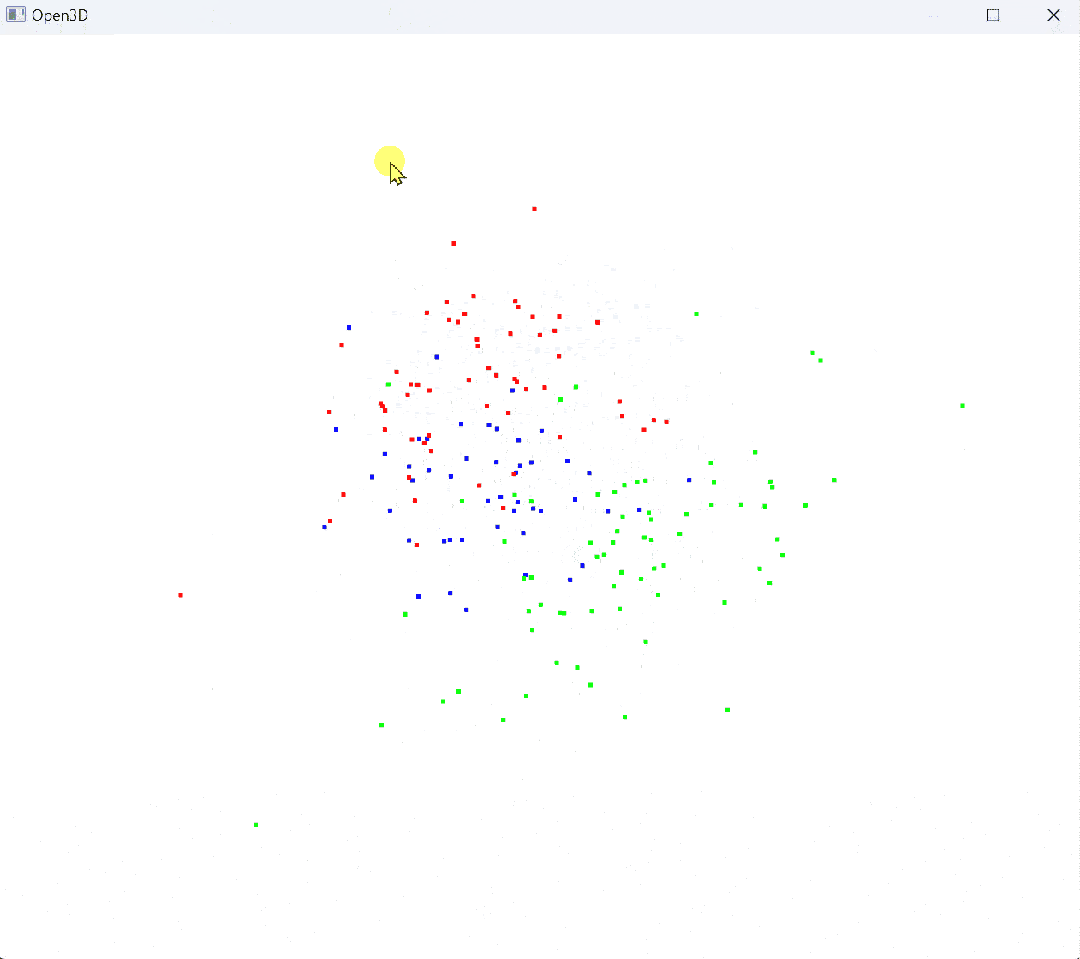
使用LDA降维到二维平面的结果：

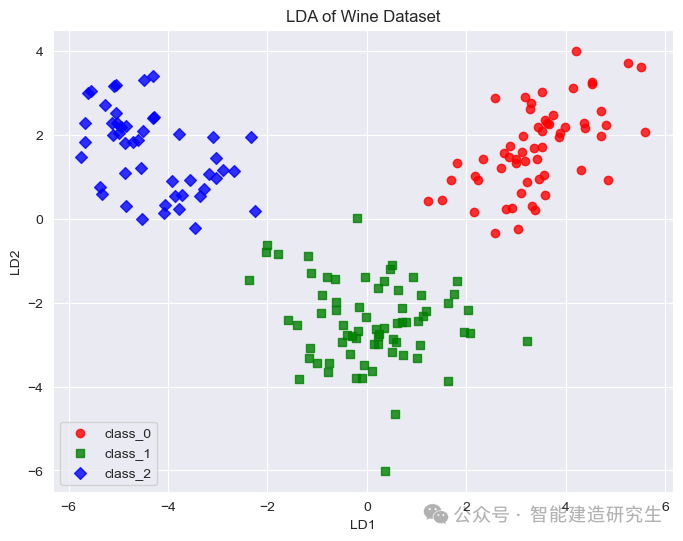
由上述结果可知，对于Wine 数据集，LDA 可以很好地区分数据，其主要原因包括：

1. 类别间的可分性：Wine 数据集的三个类别在特征空间中有明显的分布差异，LDA 可以通过投影最大化这些差异。

2. 线性判别：LDA 寻找的特征线性组合能够最大化类别间的差异，利用化学特征间的线性关系实现有效分类。

3. 数据分布：数据在特征空间中的分散和类别间的显著差异使得 LDA 能够找到最佳的投影方向。

4. 类别标签的利用：LDA 使用类别标签信息，有助于更好地了解数据的类别结构，实现有效降维和分类。

代码说明

1. 加载数据集和标准化：

   • 使用 load_wine 函数加载 Wine 数据集。

   • 使用 StandardScaler 进行数据标准化。

2. 使用 Open3D 进行降维前的三维可视化：

   • 定义一个 visualize_3d 函数，该函数接受数据和标签，并使用 Open3D 进行三维可视化。

   • 在函数中，创建一个点云对象并将前 3 个特征作为点云的三维坐标。根据标签设置不同的颜色。

   • 使用 Open3D 的可视化工具显示三维点云。

3. LDA 降维：

   • 使用 LinearDiscriminantAnalysis 进行降维，将数据降到二维。

   • 使用 Matplotlib 绘制降维后的二维散点图，不同颜色和标记代表不同的类别。

LDA 的核心是通过最大化类间散度与最小化类内散度的比值，找到最优的投影方向，从而在降维后的空间中显著分离不同类别的数据。

---

以上内容总结自网络，如有帮助欢迎转发，我们下次再见！