裴蜀定理（或贝祖定理）说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

        也就是说a和b能凑出来的最小正整数就是它们的最大公约数，它的一个重要推论是：a,b互质的充分必要条件是存在整数x,y使ax+by=1，只有a和b互质的时候才能取到等于1.

        如果从0开始每次走a步，超过b位置就模b，可能到的位置p就是ax+by=p，p是gcd（a，b）的倍数。

        ax + by = m，有解当且仅当m是d的倍数。裴蜀等式有解时必然有无穷多个整数解。

        推导：

        ax+by=gcd（a，b），在exgcd的结束条件中b等于0，此时ax+0*y=gcd（a，0）=a，所以x=1，此时的y可以取任意值，我们可以取为0.

        

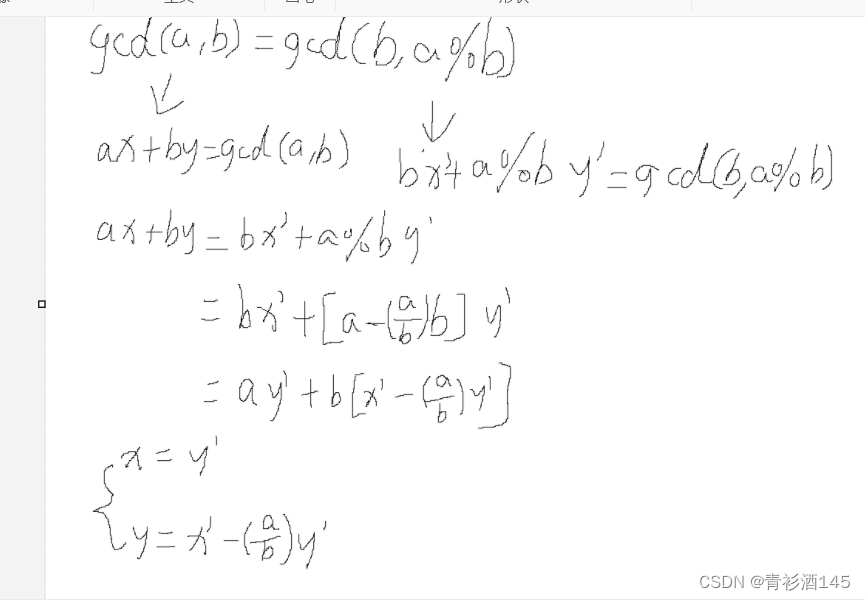
int exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1,y=0;
		return a;
	}
	int d=exgcd(b,a%b,y,x);//此时的y就是下一层的x’，x就是下一层的y’
	y-=a/b*x;//x已经是y’，y=x’（就是现在的y）-a/b*y’（就是现在的x）
	return d;
}

上面只是求了一组ax+by=gcd（a，b）的特解，怎么求其他解：

（x0，y0）是一组特解，由于gcd（a，b）相等，其他解等于这组特解

a’于b’原来有的gcd已经被除掉了，所以gcd只剩1了

结论：ax+by=d的一组特解是（x0，y0），那么通解就是（x0+kb’，y0-ka’），其中a’=a/gcd（a，b），b’=b/gcd（a，b）。

容易知道x0+kb’可以一直加减任意倍的b’，也就是说（（x0+kb’）%b’+b’）%b’就是第一次x大于等于0的时候，也就是说最小非负整数解x就是（（x0+kb’）%b’+b’）%b’

题目链接

思路：

        题目等价于求cx+py+a=b（p=2^k）的最小正整数解，即cx+py=b-a的最小正整数解

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int inf=0x3f3f3f3f;
const int N=1e5+10;
const int mod=1e9+7;
#define fi first
#define se second
#define int ll
int exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1,y=0;
		return a;
	}
	int d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}
int qpow(int a,int b){
	int res=1;
	while(b){
		if(b&1) res=res*a;
		b>>=1;
		a=a*a;
	}
	return res;
}
void solve(){
	int a,b,c,k;
	while(cin>>a>>b>>c>>k,a||b||c||k){
		int x0,y0;
		int n=qpow(2,k);
		int d=exgcd(c,n,x0,y0);
		if((b-a)%d){
			cout<<"FOREVER"<<endl;
			continue;
		}
		int t=n/d;
		int x1=x0*(b-a)/d;
		cout<<(x1%t+t)%t<<endl;
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int t=1;
	//cin>>t;
	while(t--){
		solve();
	}
	return 0;
}