目录
一、实验数学原理
二、实验算法和实验步骤
三、结果分析
1. 均方误差变化的影响
2. 迭代次数变化的影响
3. 学习效率变化的影响
四、预测
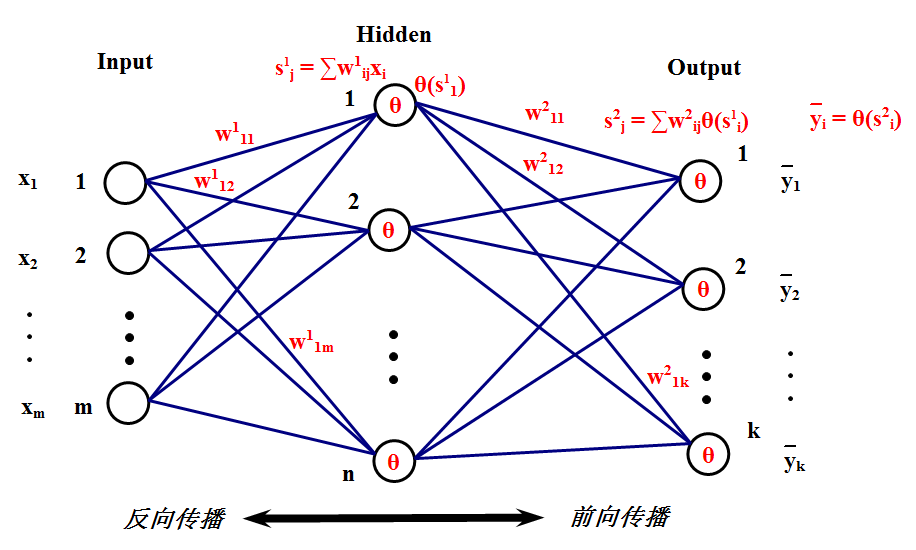
一、实验数学原理
激活函数:
一般使用S形函数(即sigmoid函数),比如可以使用log-sigmoid:
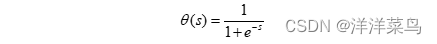
或者tan-sigmoid:

第一步,网络初始化
给各连接权值分别赋一个区间(-1,1)内的随机数,设定误差函数e,给定计算精度值和最大学习次数M。
第二步,随机选取第k个输入样本及对应期望输出:

第三步,计算隐含层各神经元的输入和输出
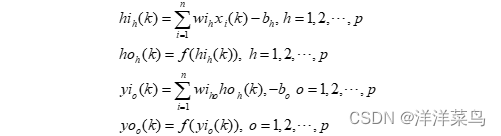
第四步,利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数

第五步,利用隐含层到输出层的连接权值、输出层的和隐含层的输出计算误差函数对隐含层各神经元的偏导数
。
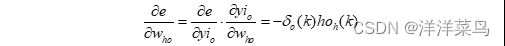
第六步,利用输出层各神经元的和隐含层各神经元的输出来修正连接权值
。
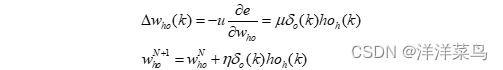
第七步,计算全局误差

第八步,判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
二、实验算法和实验步骤
1.实验算法:
输入:
过程:
输出:连接权与阈值确定的多层前馈神经网络
2.实验步骤:
1.输入数据
将训练数据输入到Matlab中,并将训练数据分为输入数据和输出数据,输入层的节点数为2,输出层的节点数为1。
2.创建网络
设定网络隐层和输出层的激活函数以及网络训练函数,隐层神经元数设为4。
3.设置训练次数和收敛误差
4.训练网络
5.进行网络预测
6.提取神经网络数学表达式
三、结果分析
1. 均方误差变化的影响

由图得当均方误差分别为1e-05, 3e-05, 5e-05, 7e-05时,模型的拟合效果无明显差距,则可忽略均方误差变化的影响。
其图中表达式依次为:

2. 迭代次数变化的影响
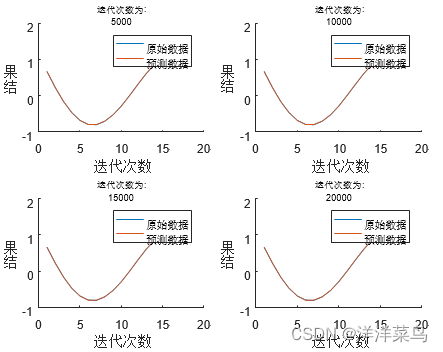
由图得当迭代次数分别为5000,10000,15000,20000时,模型的拟合效果无明显差距,则可忽略迭代次数变化的影响。
其图中表达式依次为:

3. 学习效率变化的影响

由图得当学习效率分别为0.05,0.1,0.15,0.2时,模型的拟合效果无明显差距,则可忽略学习效率变化的影响。
其图中表达式依次为:

四、预测
由三可知,可选择均方误差为0.00001,迭代次数为15000,学习效率为0.1,此时模型拟合效果较好,由此可对预测集数据进行预测,如当时,结果是多少?
不同隐层神经元个数下的模型拟合结果:

由图可知,当隐藏神经元个数不同时,拟合程度无明显差异,说明隐层神经元个数的变化对拟合效果无明显影响。
此时表达式依次为:

不同隐层神经元个数下的预测结果如表1:
表1 不同隐层神经元个数下的预测结果
| 隐层神经元个数 | 预测结果 |
| 3 | 1.255628e+00 |
| 4 | 1.059957e-05 |
| 5 | -8.677562e-01 |
| 6 | 4.536676e-01 |