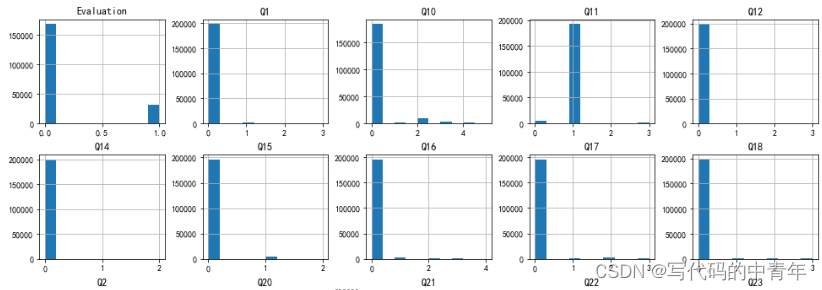
2.3 连续型随机变量

（一）定义

连续型随机变量即在一定区间内变量取值有无限个，或数值无法一一列举出来，例如某个地区男性健康成人的身高值、体重值。
如果对于随机变量X的分布函数F(X)，存在非负可积函数f(x)，使对于任意实数有：
F(X)=∫负无穷到xf(t)dt
则称X为连续型随机变量，f(X)称为x的概率密度函数，简称概率密度。

1. 非负性：概率密度函数的取值必须是非负的，即 f(x) ≥ 0。
2. 归一性：概率密度函数在整个定义域上的积分等于1，即 ∫f(x)dx = 1。
3. 区间概率：概率密度函数在某个区间上的积分表示该区间内随机变量取值的概率，即 P(a ≤ X ≤ b) = ∫[a,b]f(x)dx。

（二）常见的连续型随机变量的分布

常见的连续型随机变量分布包括均匀分布、指数分布和正态分布等。以下是这些分布的介绍和公式：

1. 均匀分布
介绍：

均匀分布是指在一个固定区间内，随机变量落在任何一点的概率都相等。这种分布常用于描述那些没有明确偏好或趋势的随机现象。
公式：

若随机变量X在区间(a,b)上服从均匀分布，则记为X~U(a,b)。
概率密度函数为：f(x) = 1/(b-a)，当a≤x≤b；f(x) = 0，当x<a或x>b。
数学期望E(X)为(a+b)/2。
方差D(X)为(b-a)^2/12。
2. 指数分布
介绍：

指数分布通常用于描述等待时间、生存时间等随机变量，这些变量的特点是“无记忆性”，即无论已经等待了多久，未来等待的时间分布都与最初相同。
公式：

若随机变量X的概率密度函数为f(x) = λe^(-λx)，x≥0；f(x) = 0，x<0，则称X服从参数为λ的指数分布，记为X~e(λ)。
数学期望E(X)为1/λ。
方差D(X)为1/λ^2。
3. 正态分布
介绍：

正态分布（也称为高斯分布）是统计学中最重要、最常用的一种连续型随机变量分布。它描述了自然界和社会中许多随机现象的分布规律，如人的身高、体重、考试成绩等。
公式：

若随机变量X的概率密度函数为f(x) = (1/√(2πσ2))e(-(x-μ)2/(2σ2))，则称X服从参数为μ和σ2的正态分布，记为X~N(μ,σ2)。
其中，μ是均值，决定了分布的中心位置；σ^2是方差，决定了分布的离散程度。
当μ=0，σ=1时，称为标准正态分布。
数学期望E(X)为μ。
方差D(X)为σ^2。

2.4 随机变量的数字特征

随机变量的数字特征是指能够刻画随机变量某些方面的性质特征的量，这些数字特征对于理解和分析随机变量的行为至关重要。以下是对随机变量数字特征的详细介绍，包括定义、公式和性质。

定义
随机变量的数字特征是指联系于它的分布函数的某些数，如平均值（数学期望）、方差、协方差、相关系数等，它们反映了随机变量在某些方面的特征。这些特征量有助于我们更深入地理解随机变量的分布规律、取值趋势以及不同随机变量之间的关系。

常见数字特征及其公式
数学期望（均值）
定义：数学期望是随机变量所有可能取值的加权平均数，反映了随机变量的平均水平。
公式：
对于离散型随机变量X，若其分布律为P{X=xk}=pk,k=1,2,…，则数学期望E(X)=∑k=1∞xkpk（要求级数绝对收敛）。
对于连续型随机变量X，若其概率密度为f(x)，则数学期望E(X)=∫−∞+∞xf(x)dx（要求积分绝对收敛）。
性质：数学期望具有线性性质，即E(aX+b)=aE(X)+b，其中a和b为常数。
方差
定义：方差是随机变量与其数学期望之差的平方的平均数，反映了随机变量的波动大小。
公式：D(X)=E[(X-E(X))^{2]。对于离散型随机变量，D(X)=∑k=1∞[xk-E(X)]}2pk；对于连续型随机变量，D(X)=∫−∞+∞[x-E(X)]^2f(x)dx。
性质：方差具有非负性，即D(X)≥0；方差还具有平方可加性，即D(aX+b)=a^2D(X)，其中a为常数，b为任意实数。
协方差
定义：协方差用于衡量两个随机变量之间的线性相关程度。
公式：Cov(X,Y)=E[(X-E(X))(Y-E(Y))]。
性质：协方差具有对称性，即Cov(X,Y)=Cov(Y,X)；协方差还满足线性性质，即Cov(aX+bY,Z)=aCov(X,Z)+bCov(Y,Z)，其中a和b为常数。
相关系数
定义：相关系数是协方差与两个随机变量标准差乘积的比值，用于描述两个随机变量之间的线性相关强度和方向。
公式：ρXY=Cov(X,Y)/(√D(X)√D(Y))。
性质：相关系数的取值范围在-1到1之间；当ρXY=1时，表示X和Y完全正相关；当ρXY=-1时，表示X和Y完全负相关；当ρXY=0时，表示X和Y不线性相关（但可能存在其他类型的相关性）。
性质
随机变量的数字特征具有多种性质，这些性质在统计分析、概率论和实际应用中发挥着重要作用。例如：

• 线性性质：数学期望和方差都具有线性性质，这有助于我们简化复杂随机变量的计算。

• 非负性：方差总是非负的，这反映了随机变量波动的固有特性。

• 对称性：协方差具有对称性，这有助于我们理解两个随机变量之间的相互作用。

• 相关性：相关系数描述了随机变量之间的线性相关强度和方向，是统计分析中常用的一个重要指标。