梯度下降法的理解

梯度下降法不是一个机器学习算法，既不是在做监督学习，也不是在做非监督学习，是一种基于搜索的最优化方法。

作用：最小化一个损失函数
梯度上升法：最大化一个损失函数

图解

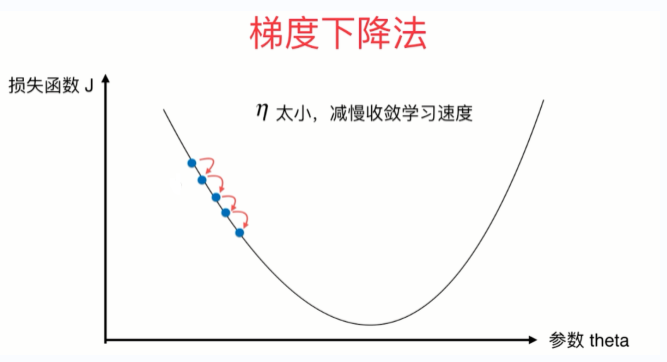
先给出一个损失函数J，在二维平面中画出的曲线如下图所示。蓝点处画的一条直线是在这一点上的导数，为负值，当theta增大，导数增大，在最低处导数为0，即为极值点，为极小值。
由上图可看出，曲线向下凹陷，可将曲线比作一个山谷，蓝点为一个球，球滚落的速度为eta（学习率），在蓝点处，theta变化相同的值时，步长会逐渐变小，因为eta逐渐变小。
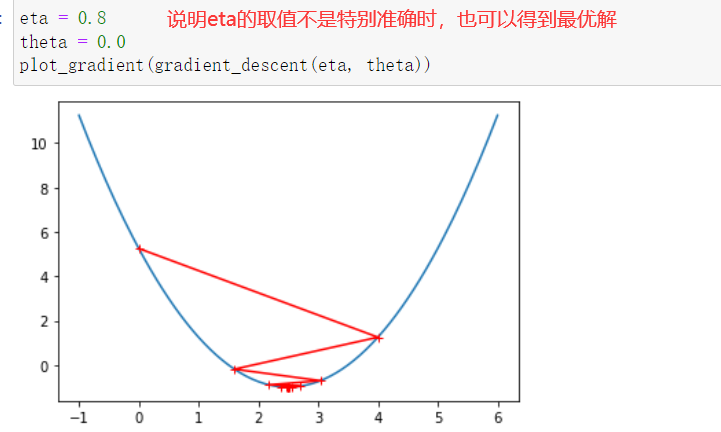
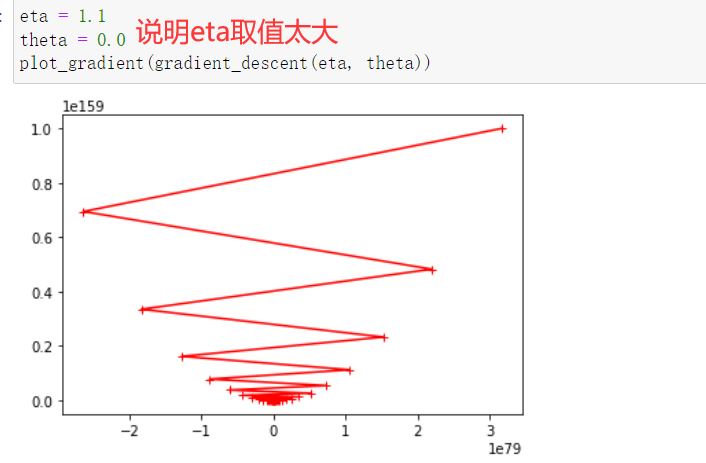
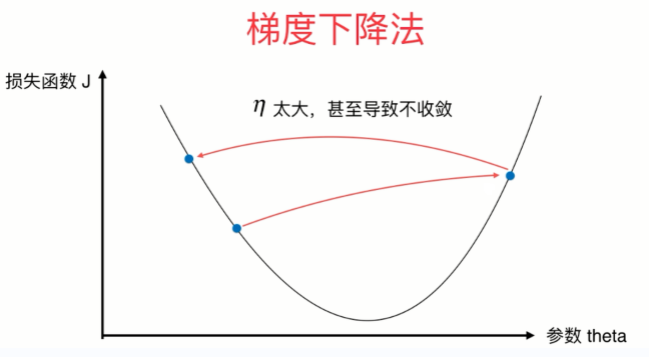
eta叫做学习率（learning rate），是梯度下降法的一个超参数。eta的取值影响我们求得最优解的速度，eta的取值过小，收留太慢，eta取值过大，可能甚至得不到最优解。

极值点和最值点

并不是所有的函数都有唯一的极值点，线性回归的损失函数具有唯一的最优解。
在这里插入图片描述

梯度下降法的求导运算

以上主要是以一个维度进行讲解，当在多维时求损失函数，其求法如下。在这里插入图片描述

公式推导

我们的主要目标是使损失函数达到最小，于是我们可以通过公式的推导，得出最终的公式。
对损失函数进行求导，并列为矩阵形式。
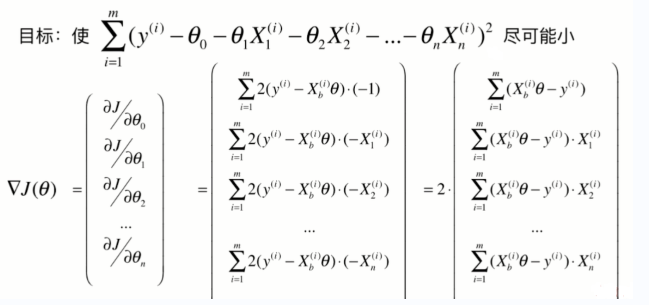
为什么要除以m？因为求和运算后本身会对数据做一个扩大的处理，有可能在我们特征数量增大的时候，求得的导数结果变得比较厉害，而求导后我们希望得到的数据跟原来的数据有很大的关系，所以要除以m。

梯度下降法的实现

先创建一个损失函数

import numpy as np
import matplotlib.pyplot as plt

plt_x = np.linspace(-1,6,141)
plt_y = (plt_x-2.5)**2-1
plt.plot(plt_x, plt_y)
plt.show()

在这里插入图片描述

写出求导函数和求值函数

def dj(theta):
    return 2*(theta-2.5) # 传入theta，求theta点对应的导数

def j(theta):
    return (theta-2.5)**2-1 # 传入theta，求theta点对应的值

找到极值点，获得对应的theta值

eta = 0.1 # 设置学习率
theta = 0.0
epsilon = 1e-8
theta_history = [theta] # 存储移动步数
while True:
    gradient = dj(theta) # 求导数
    last_theta = theta
    theta = theta - gradient*eta # theta减去步长
    theta_history.append(theta)
    if np.abs(j(theta) - j(last_theta)) < epsilon: # 小于epsilon认为到达极值点
        break
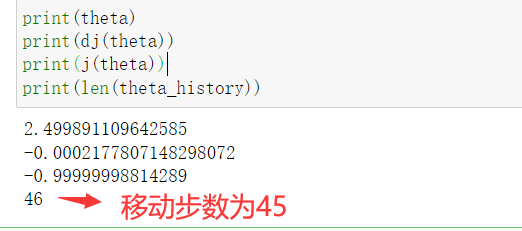
print(theta)
print(dj(theta))
print(j(theta))
print(len(theta_history))

在这里插入图片描述

在损失函数的曲线上画出移动的轨迹

plt.plot(plt_x, plt_y)
plt.plot(theta_history, [(i-2.5)**2-1 for i in theta_history], color='r', marker='+')
plt.show()

在这里插入图片描述

对以上程序进行函数封装

def gradient_descent(eta, initial_theta, n_iters=1e3, epsilon=1e-8): # n_iters为最大迭代次数
    theta = initial_theta
    theta_history = [initial_theta]
    i_iter = 1
    def dj(theta):
        try:
            return 2*(theta-2.5) # 传入theta，求theta点对应的导数
        except:
            return float('inf') # 返回一个无穷大的值
    def j(theta):
        return (theta-2.5)**2-1 # 传入theta，求theta点对应的值
    
    while i_iter<n_iters:
        gradient = dj(theta)
        last_theta = theta
        theta = theta - gradient*eta
        theta_history.append(theta)
        if np.abs(j(theta) - j(last_theta)) < epsilon:
            break
        i_iter += 1
    return theta_history

def plot_gradient(theta_history):
    plt.plot(plt_x, plt_y)
    plt.plot(theta_history, [(i-2.5)**2-1 for i in theta_history], color='r', marker='+')
    plt.show()