数据结构 -AVL树

news2024/10/7 7:24:50

文章目录

AVL树
- - 左旋和右旋
  - 插入的四种情况
  - - （一）新数字插到了左子树，导致左子树比右子树高2；左孩子的左子树比其右子树高1
    - （二）新数字插到了左子树，导致左子树比右子树高2；左孩子的右子树比其左子树高1
    - （三）新数字插到了右子树，导致右子树比左子树高2；右孩子的右子树比其左子树高1
    - （四）新数字插到了右子树，导致右子树比左子树高2；右孩子的左子树比其右子树高1
  - 插入的代码
  - 例题

AVL树

AVL 树的意义：是二分查找树 BST 。二分查找树查找某个值时，时间复杂度是 O(h) ，因此，我们让树的尽可能平衡，即最大高度尽可能的小。因此有了 AVL 。

百度百科：在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

BST 本质上是维护一个有序序列，AVL 树中的左旋右旋操作，并不会改变树的中序遍历结果。

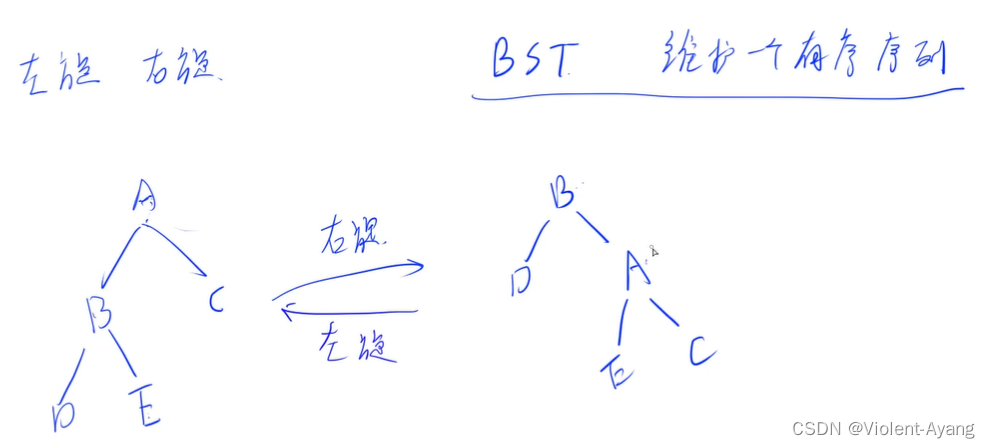
在这里插入图片描述

上图中把 A 右旋是怎么做的呢？把 B 旋转到根节点，然后把 A 变成 B 的右孩子，把 E 补偿给 A 作为 A 的左孩子。

左旋和右旋

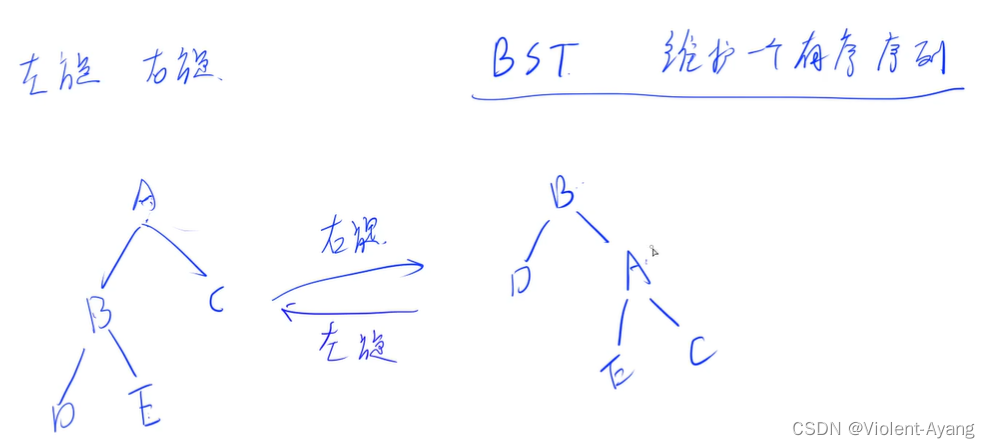
在这里插入图片描述

对节点 u 右旋：

根 u 的左儿子变成新的根 p
根的左儿子变成新的根 p 原本的右儿子
新的根 p 的右儿子变成了原本的根 u
u 和 p 的高度都需要更新

void R(int& u)
{
    int p = l[u];
    l[u] = r[p], r[p] = u;
    update(u), update(p);
    u = p;
}

对节点 u 左旋：

根 u 的右儿子变成新的根 p
根的右儿子变成新的根 p 原本的左儿子
新的根 p 的左儿子变成了原本的根 u
u 和 p 的高度都需要更新

void L(int& u)
{
    int p = r[u];
    r[u] = l[p], l[p] = u;
    update(u), update(p);
    u = p;
}

高度更新由左右儿子决定，因为求高度时，默认其两个儿子已经更新完高度了：

void update(int u)
{
    h[u] = max(h[l[u]], h[r[u]]) + 1;
}

插入的四种情况

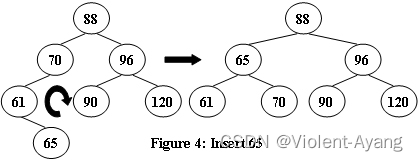
在这里插入图片描述

（一）新数字插到了左子树，导致左子树比右子树高2；左孩子的左子树比其右子树高1

对于四种情况中的①。应该右旋 A 。

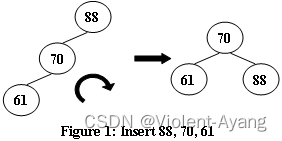
在这里插入图片描述

实例如上图，右旋 88 即可。

（二）新数字插到了左子树，导致左子树比右子树高2；左孩子的右子树比其左子树高1

对于四种情况中的③。应该左旋 B 再右旋 A 。

在这里插入图片描述

对应的情况如如下：

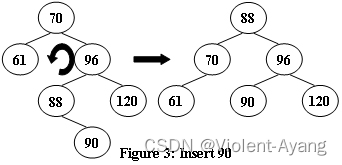
（三）新数字插到了右子树，导致右子树比左子树高2；右孩子的右子树比其左子树高1

对于四种情况中的②。应该左旋 A 。
在这里插入图片描述

对应的情况如 88 96 120 ，左旋 88 即可。

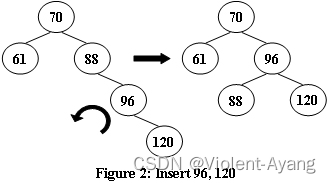
（四）新数字插到了右子树，导致右子树比左子树高2；右孩子的左子树比其右子树高1

对于四种情况中的④。应该右旋 B 再左旋 A 。

在这里插入图片描述

对应的情况如如下：

插入的代码

void insert(int& u, int w)
{
    if (!u) u = ++ idx, v[u] = w;
    else if (w < v[u])
    {
        insert(l[u], w);
        if (get_balance(u) == 2)
        {
            if (get_balance(l[u]) == 1) R(u);
            else L(l[u]), R(u);
        }
    }
    else
    {
        insert(r[u], w);
        if (get_balance(u) == -2)
        {
            if (get_balance(r[u]) == -1) L(u);
            else R(r[u]), L(u);
        }
    }

    update(u);
}