前言
基于MATLAB设计并实现了一个OFDM调制的图形用户界面(GUI)系统。该系统旨在简化OFDM调制过程的仿真,提供友好的用户交互界面。设计目标是通过GUI实现参数化的OFDM仿真,包括子载波数、符号数、IFFT长度、循环前缀长度、循环后缀长度和信噪比等参数的动态调节。系统支持多种调制方式(如QPSK、16QAM、64QAM、256QAM)和单径、多径信道模型,并实时显示OFDM信号的时域图和星座图。用户可通过GUI调整各项参数,启动或暂停仿真,观察误码率的变化。
多载波调制思想
在信道不理想的条件下,若采用单一正弦波作为载波实现调制,已调信号频带上很难保持理想传输特性,容易造成信号的严重失真和码间串扰。
多载波调制就是把数据流分解为若干个载波,因此,在多载波调制信道中,数据传输速率相对较低,码元周期较长,克服了单载波调制方式码元持续时间Ts短,占用带宽B大,信号特性不理想,易产生码间串扰等缺点。只要时延扩展与码元周期相比小于一定的值,就不会产生码间串扰,因而多载波调制对于信道的时间弥散性不敏感,具有较强的抗多径传播和抗频率选择性衰落的能力以及较高的频谱利用率。
OFDM可以抵抗多径干扰,是当前研究的一个热点。在4G移动通信等高速无线通信系统中得到了广泛的应用。
OFDM原理
OFDM时域图绘制
一个OFDM系统中有N个子信道,每个子信道采用的子载波为
其中是第k路子载波的振幅,它受基带码元的调制,
为第k路子载波的频率,
为第k路子载波的初始相位,则在此系统中的N路自信号之和可以表示为
复数形式为
代码在下面频域部分一起给出。
这一步没什么难的,就是根据公式实现。
OFDM频域图绘制
在我查过资料之后,大家基本上都是直接使用sinc绘制的。比如这下面的是来源于知乎的一篇代码生成的。
NoOfCarriers = 11; % 设定载波的数量(需要保证是奇数)
iMin = -(NoOfCarriers-1)/2; % 最小的子载波的索引
iMax = (NoOfCarriers-1)/2; % 最大的子载波的索引
f = -10:0.01:10; % 设定频率是从-10MHz到10MHz
fList = zeros(1,NoOfCarriers); % 频率列表,用来存储各sinc函数的中心频率
cList = zeros(1,NoOfCarriers); % 幅值列表,用来存储各sinc函数的幅值
%************************** 画出各OFDM子载波的频域图 **************************%
for i=iMin:1:iMax
% 计算出每一个OFDM子载波的sinc函数
fshift = i ;
c = sinc(f - fshift);
fList(i+NoOfCarriers) = fshift;
cList(i+NoOfCarriers) = max(c);
plot(f,c,'linewidth',1.5);
hold on;
stem(i ,1,'r-','linewidth',1.5);
end
xlabel("频率 MHz");
grid();
hold off;
那么为什么是sinc呢?实际上OFDM信号不可能是无限长的,而有限长的OFDM信号实际可以看做与矩形窗函数的乘积,矩形窗函数可以定义如下:
对其进行傅里叶变换:
由于时域相乘等效于频域卷积,因此OFDM信号反映到频谱,就成为各个不同位置的冲击响应与sinc函数的卷积。
这里我们来看看怎么对时域波形做fft变换。
% ======================== 绘制时域波形图 =======================
Fs = 1000; % 总的采样率
N = 1024; % 总的子载波数
T = N / Fs; % 信号绘制为一个周期的长度
x = 0 : 1/Fs : T-1/Fs; % 生成时间向量,用于绘制波形
Numscr = 4; % 绘制的子载波数量
s_data = 1; % 初始相位
y = zeros(Numscr, numel(x)); % 初始化存储每个子载波的复数值的矩阵
ini_phase = ones(1, numel(x)); % 生成与时间长度相匹配的初始相位向量
% 生成所有子载波的时域波形
for k = 0 : Numscr-1 % 循环遍历要绘制的子载波数量
y(k+1, :) = ini_phase .* exp(1i * 2 * pi * k * (0:numel(x)-1) / N); % 计算每个时间点上每个子载波的复数值
end
% 绘制时域波形
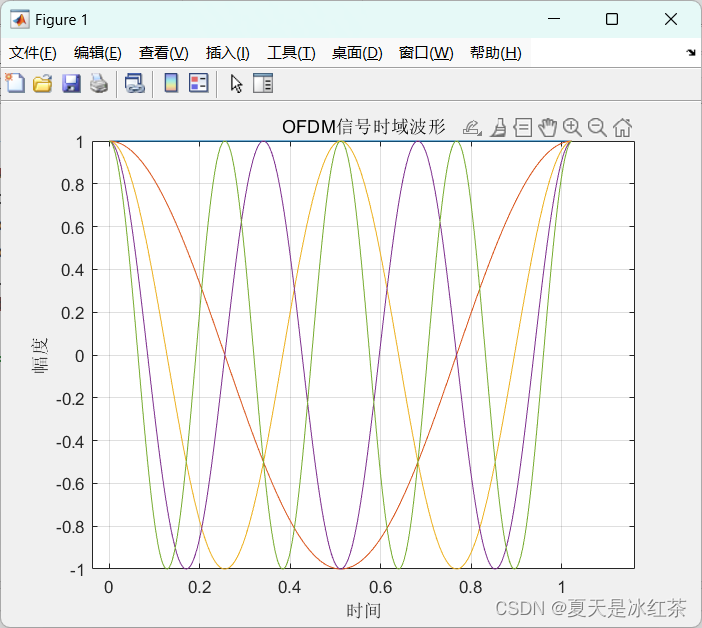
figure(1);
plot(x, real(y));
xlabel('时间/s');
ylabel('幅度/V');
title('多路子载波的时域波形');
grid on;
% ======================== 绘制频域波形图 =======================
a = 20; % 扩展系数
total_length = (a + 1) * N;
delta_f = Fs / total_length;
f = (-Fs / 2) : delta_f : (Fs / 2 - delta_f);
y1 = zeros(Numscr, a * N);
y_combined = horzcat(y, y1);
y_fft = zeros(Numscr, (a+1)*N);
for k = 1 : Numscr
y_fft(k, :) = real(fftshift(fft(y_combined(k,:)))) / N; % 计算每个子载波的频谱
end
figure(2);
plot(f, y_fft(1,:), f, y_fft(2,:), f, y_fft(3,:), f, y_fft(4,:));
grid on;
xlim([-10, 10]);
xlabel('频率/Hz');
ylabel('幅度/V');
title('多路子载波的频域波形'); a为扩展系数,设置为20,用于增加频谱的分辨率。扩展后的信号长度为 (a + 1) 倍的 N,这样就能扩展频谱分辨率,扩展后的频谱分辨率显著提高,频率间隔变得更小,频谱图更加细腻和平滑。

验证IDFT实现OFDM和模拟调制实现是否完全等效
假设OFDM系统包含了8个子载波,载波频率为1kHz,子载波频率间隔为1kHz,每个子载波采用4QAM调制,符号周期为1ms,试比较OFDM的模拟调制实现与IDFT/DFT实现。
% 参数设置
N = 8; % 子载波数
x = randi([0, 3], 1, N); % 随机生成子载波上的数据
x1 = qammod(x, 4); % 采用4-QAM调制
f = 1:N; % 子载波频率
t = 0:0.001:1-0.001; % 符号持续时间
% 模拟调制实现
w = 2*pi*f.'*t; % 子载波频率矩阵
y1 = x1 * exp(1i * w); % 模拟调制实现
% IDFT实现
x2 = ifft(x1, N); % 计算逆离散傅里叶变换
x2_time = (0:N-1)/N; % IDFT时间轴
% 绘制波形比较
figure;
plot(t, abs(y1)); % 绘制模拟调制实现的时域波形
hold on;
stem(x2_time, abs(x2) * N, '-r'); % 绘制IDFT实现的时域波形
legend('模拟调制实现','IDFT实现');
title('模拟调制实现与IDFT比较');
xlabel('时间 (s)');
ylabel('幅度');
% 验证IDFT和FFT的关系
x3 = fft(x2, N); % 计算快速傅里叶变换
disp(x1);
disp(x3);

升余弦窗处理
为了减少旁瓣干扰,提高系统的抗干扰性能,对添加了循环前缀和循环后缀的信号进行升余弦窗处理。升余弦窗处理通过调整信号的幅度,减少频域中的旁瓣,从而降低干扰。升余弦窗的系数计算使用了sin函数,目的是在窗函数的边界部分创建一个平滑的过渡。
窗口长度T由窗口的总长度bitLength和滚降系数决定:
然后,计算窗口系数window(t)其中 t 是从 1 到 的向量:
这个公式通过sin函数在窗口的边界部分创建一个平滑的过渡,以减少频谱中的旁瓣干扰。注意这里的计算方式与标准升余弦窗的公式不同,更类似于汉宁窗(Hann window)的计算方式。对于范围内的T窗口系数设置为1,表示在窗口的平坦部分,信号保持不变:
最后,将窗口反转并拼接,生成完整的升余弦窗。通过升余弦窗处理,可以有效地减少频谱中的旁瓣干扰,从而提高信号的传输质量。使用sin函数是为了在窗口的边界部分创建一个平滑的过渡,以减少干扰。尽管这里与标准升余弦窗有所不同,但其基本思想是相同的,即通过平滑过渡减少频谱旁瓣干扰。
function window = rcoswindow(alpha, bit_length)
warning off;
window = zeros(1, bit_length / 2);
t = 1:bit_length / 2;
T = bit_length / (2 * (1 + alpha));
window(t) = 0.5 * (1 - sin(pi / (2 * alpha * T) * (t - T)));
window(1:(1 - alpha) * T) = 1;
window = [fliplr(window) window]';
endOFDM实现
clear all;
close all;
% OFDM仿真参数
carrier_count = 200; % 子载波数
symbol_count = 100; % 总符号数
ifft_length = 512; % IFFT长度
CP_length = 128; % 循环前缀长度
CS_length = 20; % 循环后缀长度
alpha = 7/32; % 升余弦窗系数
SNR = 20; % 信噪比
rate = [];
% 选择调制方式:'QPSK'、'16QAM'、'64QAM'、'256QAM'
modulation_type = 'QPSK'; % 可以修改为 'QPSK', '64QAM', '256QAM'
switch modulation_type
case 'QPSK'
M = 4;
case '16QAM'
M = 16;
case '64QAM'
M = 64;
case '256QAM'
M = 256;
otherwise
error('Unsupported modulation type');
end
bit_per_symbol = log2(M);
bit_length = carrier_count * symbol_count * bit_per_symbol;
bit_sequence = randi([0, 1], bit_length, 1);
% 绘制生成随机二进制序列
figure(1);
bar(bit_sequence(1:50), 'b');
xlabel('Bit Index');
ylabel('Bit Value');
title('Binary Source Code Distribution');
grid on;
% ================子载波调制方式========================
bit_moded = qammod(bit_sequence, M, 'InputType', 'bit', 'UnitAveragePower', true);
figure('position', [0 0 400 400]);
scatter(real(bit_moded), imag(bit_moded));
title(['调制后的散点图 - ', modulation_type]);
grid on;
% ===================IFFT===========================
% =================串并转换==========================
ifft_position = zeros(ifft_length, symbol_count);
bit_moded = reshape(bit_moded, carrier_count, []);
figure('position', [400 0 400 400]);
stem(abs(bit_moded(:, 1)));
grid on;
% 1-28置零 29-228有效 229-285置零 286-485共轭 486-512置零
carrier_position = 29:228;
conj_position = 485:-1:286;
ifft_position(carrier_position, :) = bit_moded;
ifft_position(conj_position, :) = conj(bit_moded);
signal_time = ifft(ifft_position, ifft_length); % 512 100
figure('position', [0 400 400 400]);
subplot(3,1,1);
plot(signal_time(:, 1), 'b');
title('原始单个OFDM符号');
xlabel('Time');
ylabel('Amplitude');
% ==================加循环前缀和后缀==================
signal_time_C = [signal_time(end-CP_length+1:end, :); signal_time];
signal_time_C = [signal_time_C; signal_time_C(1:CS_length, :)];
subplot(3,1,2); % 单个完整符号为512+128+20=660
plot(signal_time_C(:, 1));
xlabel('Time');
ylabel('Amplitude');
title('加CP和CS的单个OFDM符号');
% =======================加窗========================
signal_window = signal_time_C .* repmat(rcoswindow(alpha, size(signal_time_C, 1)), 1, symbol_count);
subplot(3,1,3);
plot(signal_window(:, 1));
title('加窗后的单个OFDM符号');
xlabel('Time');
ylabel('Amplitude');
% ===================发送信号,多径信道====================
signal_Tx = reshape(signal_window, 1, []); % 时域完整信号
signal_origin = reshape(signal_time_C, 1, []); % 未加窗完整信号
mult_path_am = [1 0.2 0.1]; % 多径幅度
mutt_path_time = [0 20 50]; % 多径时延
path2 = 0.2 * [zeros(1, 20) signal_Tx(1:end-20)];
path3 = 0.1 * [zeros(1, 50) signal_Tx(1:end-50)];
signal_Tx_mult = signal_Tx + path2 + path3; % 多径信号
figure(5);
subplot(2,1,1);
plot(signal_Tx_mult);
title('多径下OFDM信号');
xlabel('Time/samples');
ylabel('Amplitude');
subplot(2,1,2);
plot(signal_Tx);
title('单径下OFDM信号');
xlabel('Time/samples');
ylabel('Amplitude');
% =====================发送信号频谱========================
% ====================未加窗信号频谱=======================
% 每个符号求频谱再平均,功率取对数
figure(6);
orgin_aver_power = 20 * log10(mean(abs(fft(signal_time_C'))));
subplot(2,1,1);
plot((1:length(orgin_aver_power)) / length(orgin_aver_power), orgin_aver_power);
hold on;
plot(0:1/length(orgin_aver_power):1, -35, 'rd');
hold off;
axis([0 1 -40 max(orgin_aver_power)]);
grid on;
title('未加窗信号频谱');
% ====================加窗信号频谱=========================
orgin_aver_power = 20 * log10(mean(abs(fft(signal_window'))));
subplot(2,1,2);
plot((1:length(orgin_aver_power)) / length(orgin_aver_power), orgin_aver_power);
hold on;
plot(0:1/length(orgin_aver_power):1, -35, 'rd');
hold off;
axis([0 1 -40 max(orgin_aver_power)]);
grid on;
title('加窗信号频谱');
% ========================加AWGN==========================
Rx_data_sig = awgn(signal_Tx, SNR, 'measured'); % 向单径信号添加噪声
Rx_data_mut = awgn(signal_Tx_mult, SNR, 'measured'); % 向多径信号添加噪声
% =======================串并转换==========================
Rx_data_mut = reshape(Rx_data_mut, ifft_length + CS_length + CP_length, []);
Rx_data_sig = reshape(Rx_data_sig, ifft_length + CS_length + CP_length, []);
% ====================去循环前缀和后缀======================
Rx_data_sig(1:CP_length, :) = [];
Rx_data_sig(end-CS_length+1:end, :) = [];
Rx_data_mut(1:CP_length, :) = [];
Rx_data_mut(end-CS_length+1:end, :) = [];
% FFT
fft_sig = fft(Rx_data_sig);
fft_mut = fft(Rx_data_mut);
% 降采样
data_sig = fft_sig(carrier_position, :);
data_mut = fft_mut(carrier_position, :);
figure;
scatter(real(reshape(data_sig, 1, [])), imag(reshape(data_sig, 1, [])), '.');
grid on;
title('单径下接收信号星座图');
figure;
scatter(real(reshape(data_mut, 1, [])), imag(reshape(data_mut, 1, [])), '.');
grid on;
title('多径下接收信号星座图');
% =========================逆映射===========================
bit_demod_sig = reshape(qamdemod(data_sig, M, 'OutputType', 'bit'), [], 1);
bit_demod_mut = reshape(qamdemod(data_mut, M, 'OutputType', 'bit'), [], 1);
% =========================误码率===========================
error_bit_sig = sum(bit_demod_sig ~= bit_sequence);
error_bit_mut = sum(bit_demod_mut ~= bit_sequence);
error_rate_sig = error_bit_sig / bit_length;
error_rate_mut = error_bit_mut / bit_length;
rate = [rate; error_rate_sig error_rate_mut];
% 打印误码率
fprintf('单径误码率: %f\n', error_rate_sig);
fprintf('多径误码率: %f\n', error_rate_mut);生成的波形如下所示:
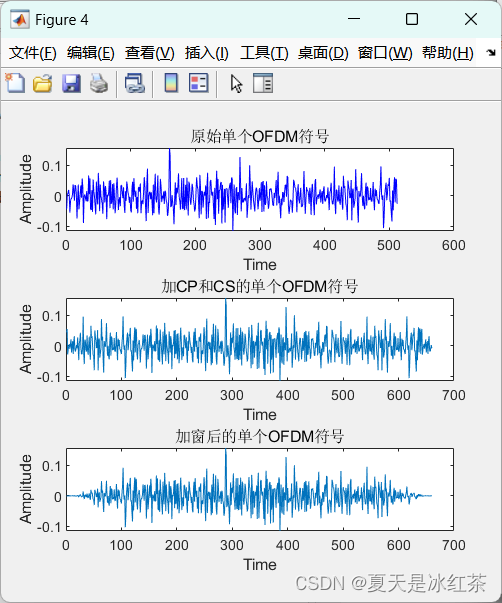
图1
图1上展示了一个原始单个OFDM符号的时域波形。该图像显示了OFDM符号在时域上的分布情况,未添加任何前缀或后缀。图1中展示了添加循环前缀(CP)和循环后缀(CS)后的单个OFDM符号。循环前缀和后缀有助于克服信道中的多径效应,并改善信号的接收性能。图1下展示了加窗后的单个OFDM符号。升余弦窗的应用使信号在边缘处更加平滑,从而减少频谱泄漏和旁瓣干扰。

图2 单径与多径下OFDM信号
图2展示了单径和多径情况下的OFDM信号。多径效应引入了信号的时延和幅度变化,导致信号波形在多径情况下更加复杂。这部分仿真展示了信号在不同传输环境下的变化。

图3 加窗子与未加窗信号频谱图对比
图3展示了加窗和未加窗信号的频谱对比。通过比较可以看到,加窗后的信号频谱在边缘部分有显著的改善,表明升余弦窗在减少频谱泄漏方面的有效性。

图4 单径与多径下接受信号星座图
图4展示了单径和多径情况下的接收信号星座图。在单径情况下,接收的星座点较为集中,表示信号失真较小;而在多径情况下,由于多径效应的影响,星座点出现了明显的散布,显示出信号在复杂信道环境下的失真程度。
用户界面设计
界面整体设计采用两栏式设计,左侧为参数设置模块,右侧为结果显示模块。
左侧的参数设置模块提供了多个输入控件,用户可以在这里设置信噪比(SNR)、子载波数、符号数、IFFT长度、循环前缀长度、循环后缀长度以及调制方式等参数。这些控件包括文本框、下拉菜单和旋钮,用户可以通过这些控件输入或选择相应的数值和选项,以便精确地控制OFDM系统的仿真环境。在参数设置模块,还设计了开始仿真、暂停(恢复)仿真和结束仿真的按钮。用户点击“开始仿真”按钮后,系统会根据设置的参数启动仿真过程。在仿真进行中,用户可以通过“暂停”按钮暂时中止仿真,通过“恢复”按钮继续仿真,而点击“结束仿真”按钮则可以完全停止当前的仿真过程。
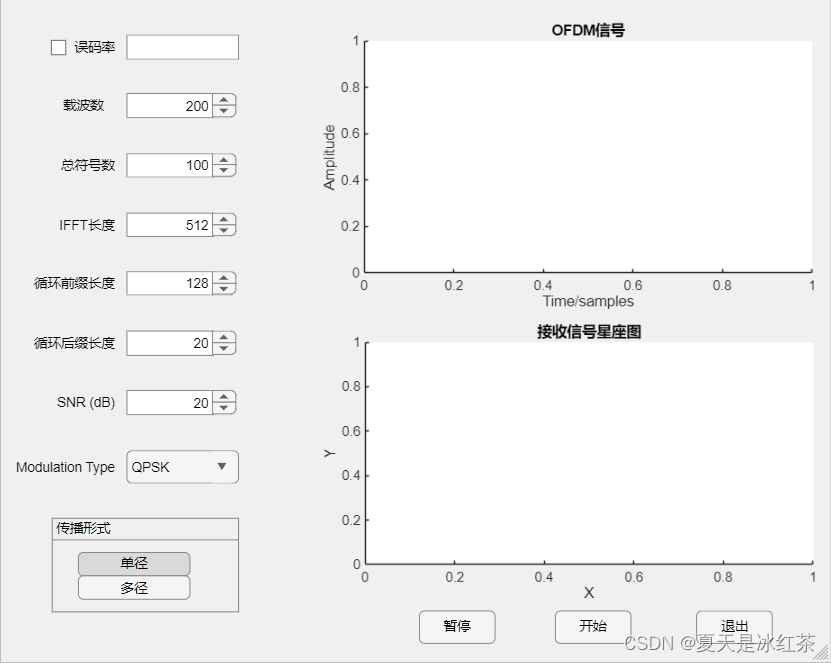
右侧的结果显示模块主要用于展示OFDM信号的时域波形和接收信号的星座图。在仿真过程中,系统会实时更新结果显示模块的内容,以便用户可以直观地观察OFDM信号的变化和传输效果。通过时域波形图,用户可以看到经过IFFT变换后的信号时域表现;通过星座图,用户可以分析接收信号的解调效果和误码情况。此外,结果显示模块还会实时显示系统的误码率,帮助用户评估不同参数设置下系统的性能。
动态演示
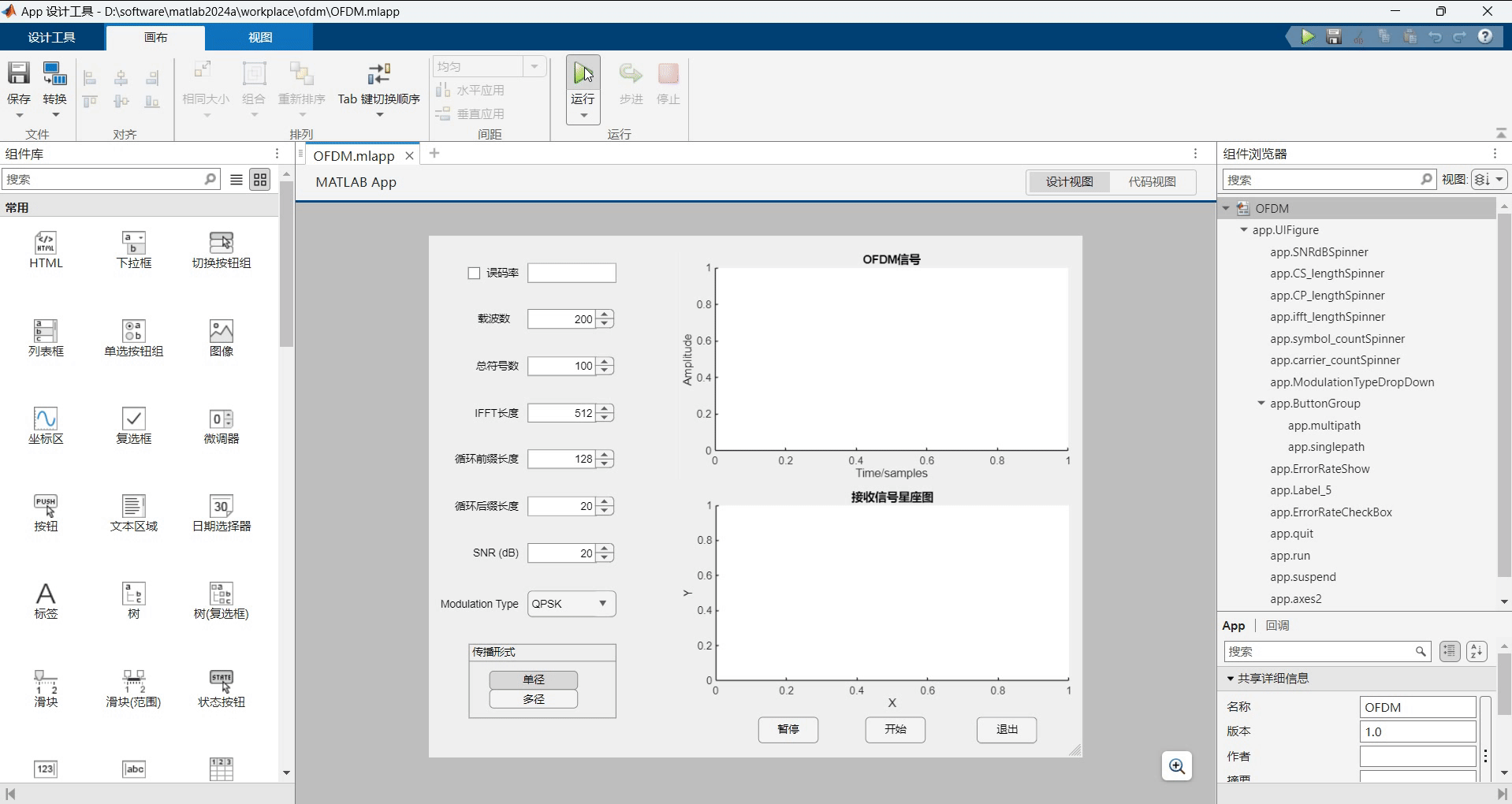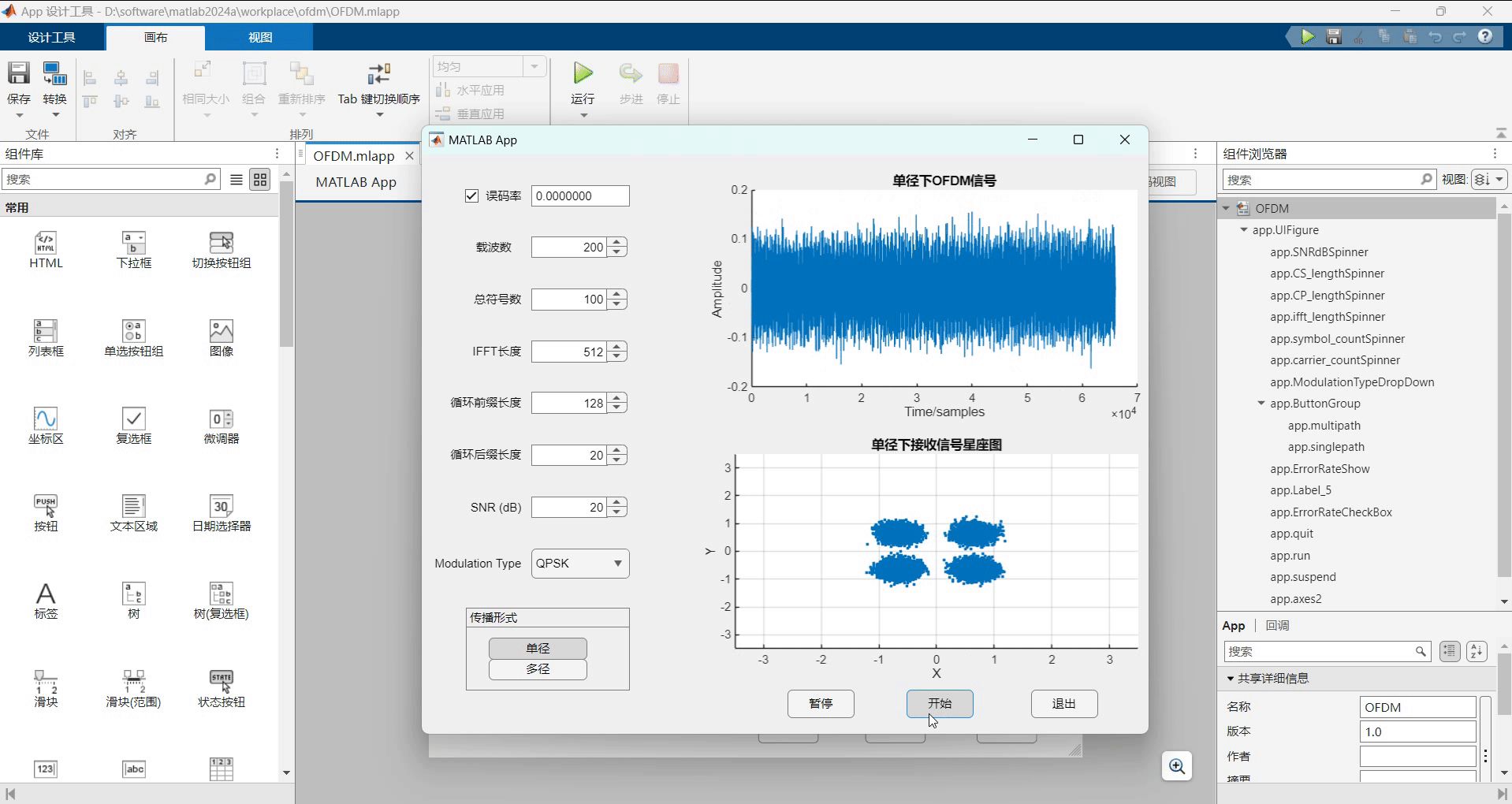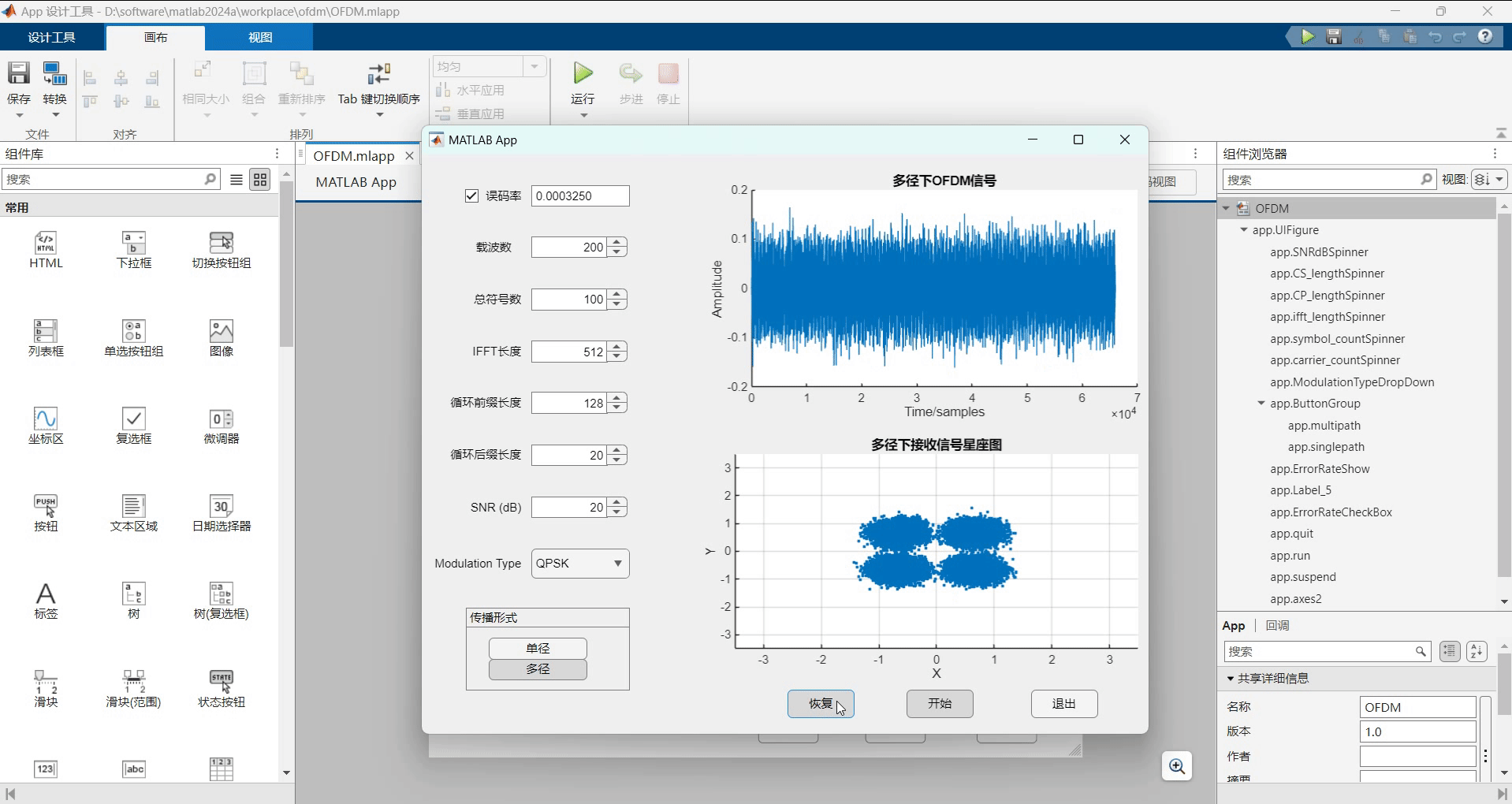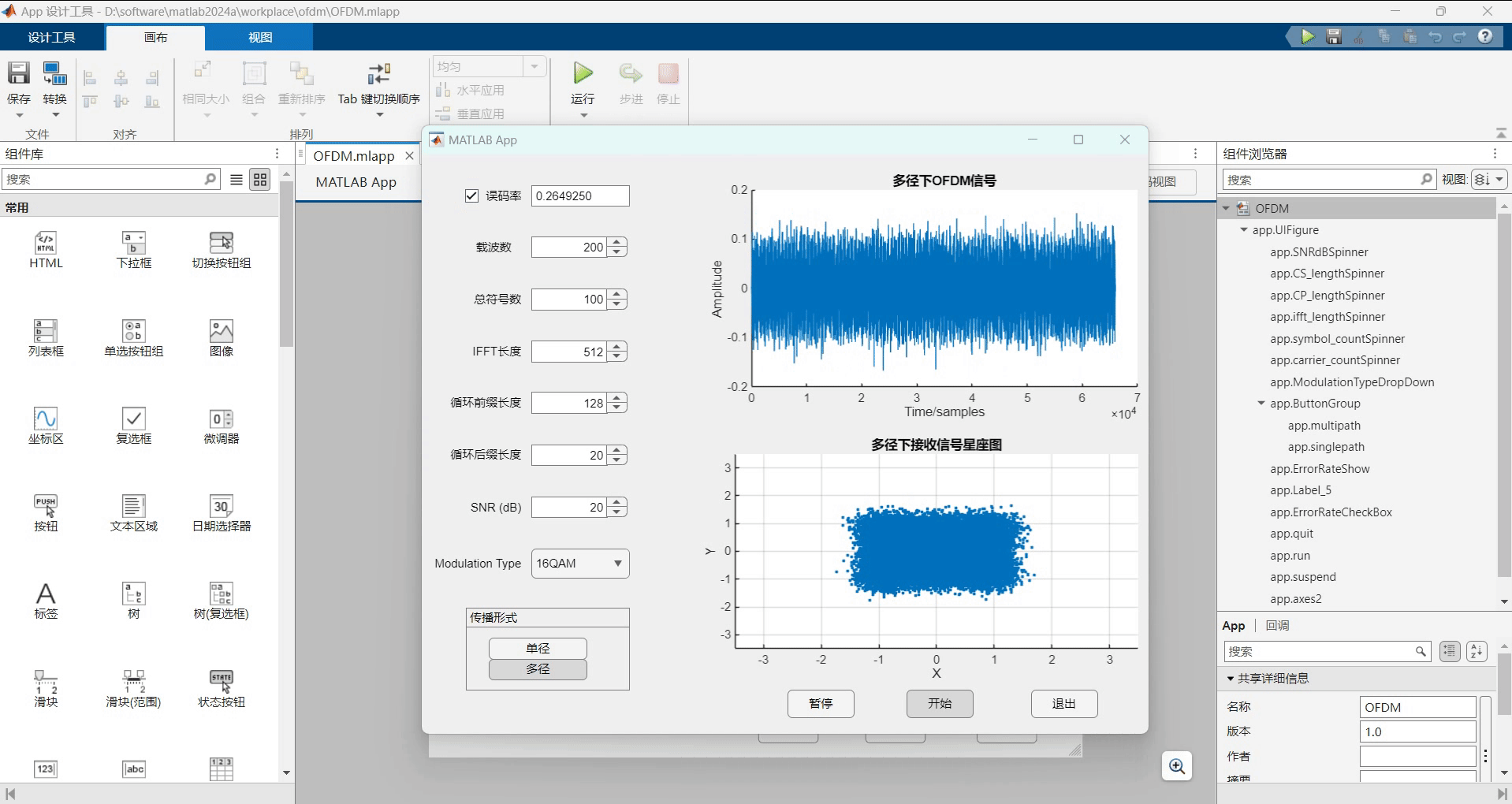
项目资源
你可以通过github下载整个项目资源。包括程序版本与独立桌面版本。
Auorui/Design-of-OFDM-GUI: 基于matlab的OFDM GUI设计 (github.com)
由于为了方便,误码率的计算是通过每次勾选复选框进行计算的。它并不是实时的,在多径上面误码率较大。
参考文章
nayakanuj/playingWithOFDM(github.com)
OFDM基本原理_ofdm信号-CSDN博客
OFDM通信系统的MATLAB仿真(2) - 羽扇纶巾o0 - 博客园 (cnblogs.com)
OFDM调制matlab仿真详细代码_ofdm matlab-CSDN博客
如何画OFDM频谱图-CSDN博客
OFDM系统仿真【matlab代码】-CSDN博客
无线通信基础2:深入理解OFDM(含Matlab代码) - 知乎 (zhihu.com)
【现代数字传输】OFDM的原理讲解和MATLAB实现_ofdm matlab-CSDN博客
OFDM学习--第二节 用Matlab仿真基本的链路_哔哩哔哩_bilibili
给“小白”图示讲解OFDM的原理(受益匪浅,OFDM小白强推)_直观图解ofdm原理-CSDN博客
OFDM系统仿真【matlab源码】_ofdmmatlab仿真代码-CSDN博客
OFDM完整仿真过程及解释(MATLAB) - 简书 (jianshu.com)
OFDM原理及MATLAB仿真-CSDN博客
OFDM演示GUI_哔哩哩_bilibili