ROS学习笔记(18):建图与定位（2）

news2024/12/28 4:44:17

0.前言

上文提到现在的我们已经进入到了SLAM领域的学习，会涉及到大量专业知识，作为一个自学的大三（好吧也快大四了）萌新并不能保证每次文章的专业性和准确性，所以，本人推荐大家能自己去查阅一些相关书籍和论文，并不关乎你一定要在多短的时间内学会这门课程，更希望大家能更热爱学习的感觉而不是只关注如何短期获取得成绩快感。

1.扫描匹配

在谷歌的SLAM算法Cartographe当中扫描匹配相当重要的一个模块。

1.扫描匹配的作用

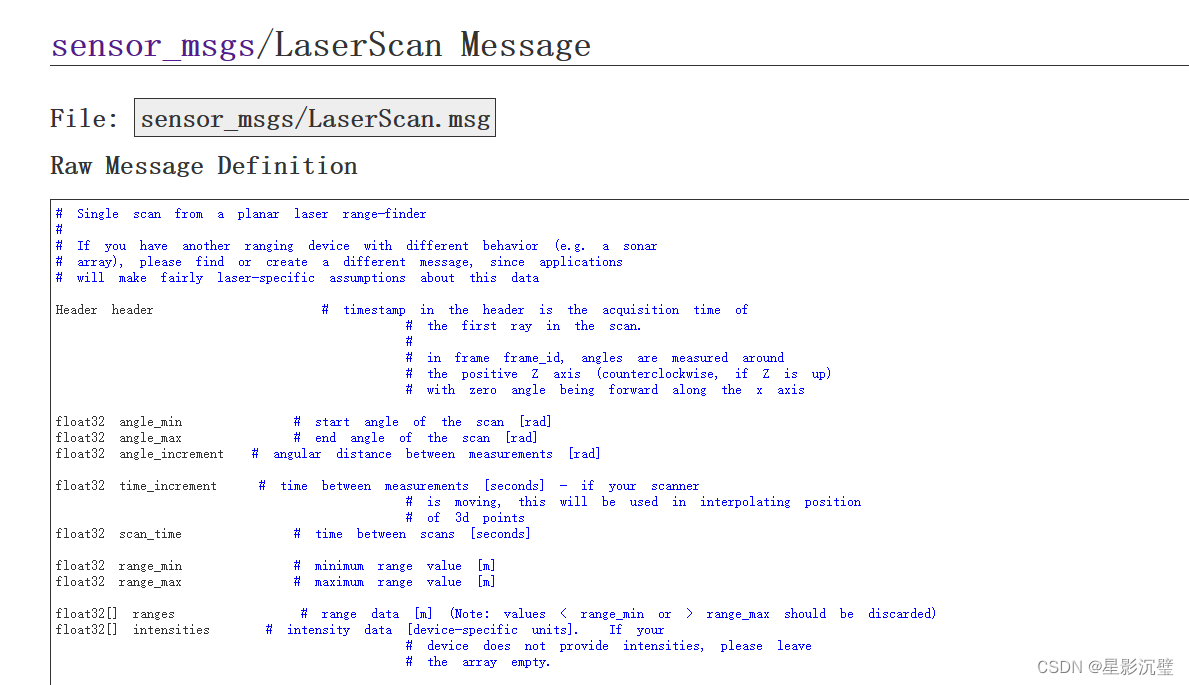
1.参看上图可知雷达的扫描是以一个固定的弧度增量来进行扫描的，这种扫描方式是由一个个不连续的点构成的，即使我们看着很像是连续的（因为他足够密集），但slam地图的构建必须保证地图的连续性（地图不能在某个地方断开，这样就是一堵墙出现了一个小洞一样），扫描匹配就需要将雷达获取到的一个个不连续的点进行连接是生成一条条连续的线，并且尽可能的与现实贴合，这就是ros的点云。

2.移动机器人是会移动的，当移动机器人位姿变化时，雷达扫描到的环境就出现了变化（如下图1），还是一样的，我们希望地图是连续的，匹配扫描就需要将位姿变化前的地图和位姿变化后的地图进行匹配，使他们连续起来，这里就是使用最大特征提取的办法了。

图1

注释：实际的实现方式请自行翻看相关书籍或论文。

2.扫描匹配一些轶事

轶事1：高速位姿改变

激光雷达和摄像头是按照一定时间进行一次数据采集的，当移送机器人的位姿改变过快时，就会产生上一次的采集数据和下一次采集的数据完全没有相同特征点，这时就完全无法进行特征匹配了。（当然随着雷达和摄像头的不断迭代，这种情况越来越少了。）因此想要提高扫描的匹配度，要么提高设备的性能，要么降低速度。

轶事2：场景高度重复

当移动机器人出现在一个高度重复的场景里时，机器人是很难判断自己是否进行了位姿改变的（有点像鬼打墙），高度相似的特征是的地图拼接十分困难。（当然这种情况极少出现。）

以下就是因移动机器人位姿改变导致扫描匹配效果差的图片：

2.使用ICP的扫描匹配

ICP(Iterative Closest Point)，中文称为迭代最近点，主要使用在点云配准，目标是计算两个点云间的变换。

网上有大佬对ICP的解读：

【PCL】—— 点云配准ICP(Iterative Closest Point)算法_icp点云配准-CSDN博客

这让我想起了数字化中国一些古老建筑和文物。

1.ICP的原理

使用蓝色和红色的点进行连线排列，这些线段就是点云（point cloud）。

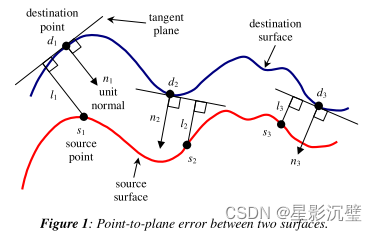
拥有了点云后，蓝色线点云上的每个点都开始寻找红色线点云上与他最近的点，这一步通常称为数据关联。找到了这些点之后进行变换，使这些点云尽可能的重叠到一起。在不断的迭代过后使得点云间的距离不再变换或达到某个可接受的阈值。

注释：最小距离计算和变换是分开进行的，第一步是计算点云的质心，这可以方便后一步的点云的相互变换，第二步就是用奇异值分解（SDV）来计算出本次变换的最佳变换。当匹配效果最佳时，点云的协方差将是最小。（当然通常不使用spd而是使用最小二乘法来进行不断的迭代，直到结果达到阈值。）

ICP迭代的目标就是找到 $M_{opt}$ :

$M_{opt}=argmin_{M} \sum_{i}((M\cdot s_i-d_i)\cdot n_i)^2$

注释：有空我来手算一遍这个公式。

2.扫描重叠机制

机器人处在一个环境当中时，会有两种确立扫描标记点的位姿的坐标，一种是以环境中某个固定点为基准坐标建立的全局坐标系；另一种是以机器人为基准坐标建立的本地坐标系。

下图2为机器人在某位姿情况下对A、B、C三点进行扫描后映射在两种不同坐标系下的状态：

图2

下图3为机器人进行位姿调整后，重新获取到同样的点在两种坐标系下的状态：

图3

通过观察机器人位姿变换前后两种坐标系中三点的的状态，可以快速发现使用全局坐标系时同样的点在坐标系下的状态是一致的；使用局部坐标系时同样的点在坐标系下的状态发生了改变，下图为使用局部坐标系下的机器人获取到的点状态情况。

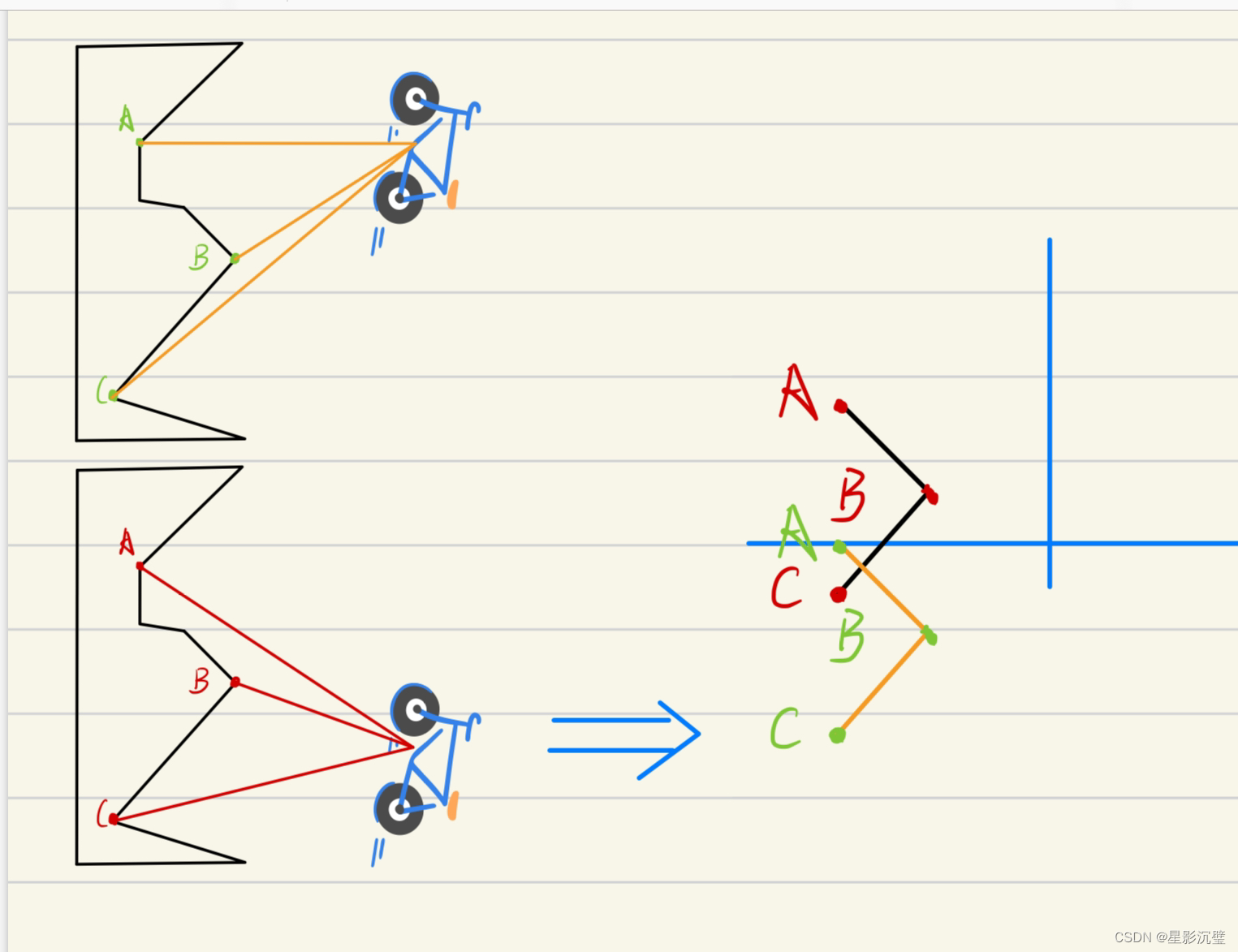图3

既然使用局部坐标系发生位姿变换时，同样的点在坐标系的状态不一样，那就需要进行扫描匹配将同样的点的状态进行统一重叠，这一步也就是将局部坐标系构建成全局坐标系（可理解为以第一个局部坐标系为全局坐标系，后续的局部坐标系都进行里程计等传感器进行数据采集后计算出相对变换），如下图是未将同样的点进行扫描匹配时产生的情况：